


4.3 The anthropic principle
The anthropic principle [171, 172] is essentially the idea that some of the parameters characterizing the universe we observe may not be determined directly by the fundamental laws of physics, but also by the truism that intelligent observers will only ever experience conditions which allow for the existence of intelligent observers. Many professional cosmologists view this principle in much the same way as many traditional literary critics view deconstruction - as somehow simultaneously empty of content and capable of working great evil. Anthropic arguments are easy to misuse, and can be invoked as a way out of doing the hard work of understanding the real reasons behind why we observe the universe we do. Furthermore, a sense of disappointment would inevitably accompany the realization that there were limits to our ability to unambiguously and directly explain the observed universe from first principles. It is nevertheless possible that some features of our world have at best an anthropic explanation, and the value of the cosmological constant is perhaps the most likely candidate.
In order for the tautology that ``observers will only observe
conditions which allow for observers'' to have any force,
it is necessary for there to be alternative conditions -
parts of the universe, either in space, time, or branches of the
wavefunction - where things are different. In such a case, our
local conditions arise as some combination of the relative
abundance of different environments and the likelihood that
such environments would give rise to intelligence. Clearly,
the current state of the art doesn't allow us to characterize
the full set of conditions in the entire universe with any
confidence, but modern theories of inflation and quantum
cosmology do at least allow for the possibility of widely
disparate parts of the universe in which the ``constants of
nature'' take on very different values (for recent examples see
[173,
174,
175,
176,
177,
178,
179].
We are therefore faced with the task of estimating quantitatively
the likelihood of observing any specific value of
 within such a scenario.
within such a scenario.
The most straightforward anthropic constraint on the vacuum
energy is that it must not be so high that galaxies never
form [180].
From the discussion in
Section (2.4), we know that overdense
regions do not
collapse once the cosmological constant begins to dominate
the universe; if this happens before the epoch of galaxy formation,
the universe will be devoid of galaxies, and thus of stars and
planets, and thus (presumably) of intelligent life. The
condition that

 (zgal)
(zgal)

 M(zgal) implies
M(zgal) implies
where we have taken the redshift of formation of the first
galaxies to be zgal ~ 4. Thus, the cosmological
constant could be somewhat larger than observation allows and
still be consistent with the existence of galaxies. (This
estimate, like the ones below, holds parameters such as the
amplitude of density fluctuations fixed while allowing
However, it is better to ask what is most likely value of
where P*(
Thus, if one is willing to make the leap of
faith required to believe that the value of the cosmological
constant is chosen from an ensemble of possibilities, it is
possible to find an ``explanation'' for its current value (which,
given its unnaturalness from a variety of perspectives, seems
otherwise hard to understand). Perhaps the most significant
weakness of this point of view is the assumption that there
are a continuum of possibilities for the vacuum energy density.
Such possibilities correspond to choices of vacuum states
with arbitrarily similar energies. If these states were
connected to each other, there would be local fluctuations which
would appear to us as massless fields, which are not observed
(see Section 4.5). If on the other hand
the vacua
are disconnected, it is hard to understand why all possible values
of the vacuum energy are represented, rather than the differences
in energies between different vacua being given by some
characteristic particle-physics scale such as
MPl or MSUSY. (For one scenario featuring
discrete vacua with densely spaced energies, see
[187].)
It will therefore (again) require advances in our understanding
of fundamental physics before an anthropic explanation for the
current value of the cosmological constant can be accepted.


 to vary; depending on one's
model of the
universe of possibilities, it may be more defensible to vary
a number of parameters at once. See for example
[181,
182,
172].
to vary; depending on one's
model of the
universe of possibilities, it may be more defensible to vary
a number of parameters at once. See for example
[181,
182,
172].

 , i.e. what
is the value that would
be experienced by the largest number of observers
[183,
184]?
Since a universe with
, i.e. what
is the value that would
be experienced by the largest number of observers
[183,
184]?
Since a universe with

 0 /
0 /
 M0 ~ 1 will have many
more galaxies than one with
M0 ~ 1 will have many
more galaxies than one with

 0 /
0 /
 M0
~ 100, it is quite conceivable that most observers will
measure something close to the former value. The probability
measure for observing a value of
M0
~ 100, it is quite conceivable that most observers will
measure something close to the former value. The probability
measure for observing a value of

 can be decomposed as
can be decomposed as
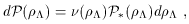

 )
d
)
d
 is
the a priori probability measure (whatever that might
mean) for
is
the a priori probability measure (whatever that might
mean) for 
 , and
, and
 (
(
 )
is the average number of galaxies which form at the specified
value of
)
is the average number of galaxies which form at the specified
value of 
 .
Martel, Shapiro and Weinberg
[185]
have presented a calculation of
.
Martel, Shapiro and Weinberg
[185]
have presented a calculation of
 (
(
 ) using a spherical-collapse model.
They argue that it is natural to take the a priori
distribution to be a constant, since the allowed range of
) using a spherical-collapse model.
They argue that it is natural to take the a priori
distribution to be a constant, since the allowed range of

 is very far from what we would expect from particle-physics
scales. Garriga and Vilenkin
[186] argue on
the basis of quantum cosmology that there can be a significant
departure from a constant a priori distribution. However,
in either case the conclusion is that an observed
is very far from what we would expect from particle-physics
scales. Garriga and Vilenkin
[186] argue on
the basis of quantum cosmology that there can be a significant
departure from a constant a priori distribution. However,
in either case the conclusion is that an observed

 0 of the same order of
magnitude as
0 of the same order of
magnitude as
 M0 is by no means
extremely unlikely (which is
probably the best one can hope to say given the uncertainties
in the calculation).
M0 is by no means
extremely unlikely (which is
probably the best one can hope to say given the uncertainties
in the calculation).