4. LARGE-SCALE STRUCTURE

Results on large-scale structure (LSS) were reported by a number of speakers at the conference. [Sutherland] described a determination of the power spectrum of galaxy fluctuations from the IRAS-based Point Source Catalogue redshift survey (PSCz). Using a sample of 14,500 galaxies with 60 µm flux of more than 0.6 Jy covering 84% of the sky, the PSCz team find that they are able to determine the power spectrum, P(k), for wavenumbers down to 0.03 h Mpc^-1 (i.e. scales up to 200 h^-1 Mpc). The results (Sutherland et al. 1999, Tadros et al. 1999) are consistent with the earlier QDOT and 1.2 Jy surveys, although P(k) is significantly better determined. For plausible values of the small-scale velocity dispersion, P(k) is well-fit by a CDM-like model with shape parameter 0.25 and normalisation ₈ 0.75 (although assuming a larger dispersion permits a model with 0.5 to be marginally acceptable).

[Rowan-Robinson] reported an estimate of = ^0.6 / b derived from the comparison of the Local Group (LG) motion with respect to the CMB and the motion predicted from a model based on clusters and voids identified in the PSCz and the literature (see also Schmoldt et al. 1999a, 1999b). The predicted LG dipole has nearly converged by z = 0.1 (with most of the LG motion generated within 200 h^-1 Mpc); linear theory requires 0.7 to fit the observed amplitude of the LG motion.

[Guzzo] summarised the results of the ESO Slice Project ESP; Vettolani et al. 1997) redshift survey. This pre-cursor to surveys like the 2dFGRS used photographic sky survey plates to select a sample of galaxies down to b_J = 19.4 in a single 1° x 35° strip. Redshifts were obtained for 3342 galaxies (85% complete; Vettolani et al. 1998). Perhaps the most significant LSS result to emerge from ESP, is that there is good evidence for a local under-density of nearly a factor of 2 extending out to 250 h^-1 Mpc (Zucca et al. 1997). This is consistent with the normalisation difference between the luminosity functions derived from surveys at this depth (ESP itself and the Autofib survey, Ellis et al. 1996) and those derived from shallower surveys such as APM-Stromlo (Loveday et al. 1992). It also `explains' the origin of the steep number counts at bright magnitudes (Maddox et al. 1990), although it begs the question of the completeness of the galaxy catalogues derived from photographic surveys at bright magnitudes. The local void implied by this result would appear to cover much of the south Galactic cap, as evidenced by the north/south difference in galaxy density found in the PSCz, LCRS and CfA2 surveys. Is this void, with an amplitude / ~ 0.5 compatible with statistical measures of clustering? The ESP redshift-space correlation function is in good agreement with other determinations on scales between 1 and 50 h^-1 Mpc, though a little lower on the smaller scales. The power spectrum is likewise consistent with other determinations at wavenumbers k > 0.1 h Mpc^-1. However the small volume covered by the survey, and its strip geometry, prevent a reliable determination of P(k) at wavenumbers below about 0.1 h Mpc^-1 (i.e. scales above 60 h^-1 Mpc).

An efficient approach to surveying larger volumes, and so measuring P(k) at smaller k, is to use redshift surveys of clusters, since clusters are about 5x more strongly clustered than galaxies. Results from two such surveys were summarised at the meeting. [Boehringer] and [Guzzo] reported early results from the REFLEX survey, while [Tadros] summarised the results from the first stage of the APM cluster survey.

[Boehringer] noted the advantages of an X-ray selected cluster sample as being the close correlation between L_X and mass, and the minimisation of projection effects. He described the detection of clusters in the ROSAT All Sky Survey for the REFLEX (southern) and NORAS (northern) samples (Guzzo et al. 1999). Together these samples comprise over 900 clusters covering the whole sky at latitudes b > |20°| down to a flux limit of F_X = 3 x 10^-12 erg s cm². The preliminary power spectrum derived from the REFLEX survey using a subset of 188 clusters in a 400 h^-1 Mpc co-moving cube (Schuecker et al. 1998) appears to show a significant turnover in P(k) at k 0.04-0.05 h Mpc^-1, corresponding to 125-160 h^-1 Mpc. [Guzzo] presented very preliminary results from a larger sample of clusters in a 1000 h^-1 Mpc comoving cube which confirm the turnover in P(k). But the newer results also hint at a possible second peak in P(k) at k ~ 0.01, although a = 0.7 flat CDM model remains consistent within the (large) uncertainties.

[Tadros] described a similar survey, the APM Cluster Redshift Survey (Tadros et al. 1998). The first phase of this survey consisted of 364 clusters drawn from the APM cluster catalogue of 960 clusters covering 4500 sq.deg. The APM clusters provide a cleanly-selected sample that is largely unaffected by the inhomogeneities and projection effects afflicting the Abell catalogue. The redshift-space cluster-cluster correlation function _cc(s) is well represented by a power law with index ~ 2 and a correlation length of 14 h^-1 Mpc (smaller than that of the Abell catalogue). The LSS as measured from clusters provides a clean comparison with cosmological models, since clusters are readily identified from the dark matter halos without the confusion of a bias parameter. The APM _cc(s) is consistent with CDM and MDM models, but has more clustering than is predicted by standard CDM.

An estimate of = ^0.6 / b can be obtained by comparing the real-space and redshift-space cluster-galaxy cross-correlation functions _cg. The real-space _cg(r) was derived from the cluster survey and the APM galaxy catalogue by inverting the angular cluster-galaxy cross-correlation function. The redshift-space _cg(, ), as a function of separation in the plane of the sky () and along the line of sight (), was derived from the cluster survery and the Stromlo-APM redshift survey. These two _cg's can be related using a model incorporating non-linear infall and the velocity dispersion of galaxies around clusters. [Tadros] showed that the best-fit model yields an estimate of 0.4, with a 95% upper confidence limit of < 0.7. The power spectrum from the APM cluster survey shows a turnover at k 0.03 h Mpc^-1, but the median depth of the survey (270 h^-1 Mpc) is only just adequate to measure P(k) on this 200 h^-1 Mpc scale. To improve the significance of this detection and reduce the systematic errors, the second phase of the APM cluster survey, now underway, will obtain redshifts for the remaining clusters in the APM cluster catalogue, bringing the sample up to 960 clusters. This cluster survey, which will take 2-3 years to complete, will be particularly useful since it overlaps with the 2dF Galaxy Redshift Survey.

The faint galaxy correlation function at large angular scales was discussed by [Brown], who has used digitally-stacked Schmidt plates to achieve an approximate limit of B_J = 23.5. This gives 700,000 galaxies in each of two 40 sq.deg fields. The median redshift at this depth is z 0.4. The correlation function he derives is well-fit as a power-law, () ^1- with = 1.7, over the range 0.05-10 h^-1 Mpc. The amplitude of the correlation function declines as (1 + z)^-(3+) with 0, corresponding to fixed clustering in physical coordinates. However these results hide the different clustering properties of the red and blue galaxies, which are respectively fitted by models with = 1.8, = -1.3 and scalelength r₀ = 8.6 h^-1 Mpc, and = 1.6, = -1.5 and r₀ = 3.5 h^-1 Mpc. The clustering amplitude of red galaxies is thus about 5x higher than the blue galaxies. The lack of any significant strengthening of the clustering amplitude of blue galaxies out to z ~ 0.4 suggests that the increase in the population of blue galaxies in clusters with redshift (the Butcher-Oemler effect) is simply related to the overall increase in the faint blue galaxy population with redshift.

The LSS goals of the 2dFGRS, and some preliminary results from the survey, were described by [Dalton]. The main LSS goals are: (i) the determination of P(k) on large scales ( > 100 h^-1 Mpc); (ii) the topology of the 3D distribution; (iii) tests of gaussianity (on large scales) and biasing (on small scales) from higher-order statistics; (iv) estimation of the mass density and the bias parameter(s) b from the redshift-space distortions. Dalton discussed the tiling and fibre-assignment algorithms used in the survey, and showed that the restrictions on minimum fibre separations mean the survey is significantly biased against close pairs with separations less than 2 arcmin (corresponding to 150 h^-1 kpc at the median depth of the survey, z = 0.1). This effect, and the variation in redshift completeness with apparent magnitude, are taken into account when estimating or simulating the large-scale structure statistics derived from the survey.

[Dalton] showed preliminary determinations of the redshift-space correlation function (, ) for the 2dFGRS. There is very good agreement with the results obtained from the Las Campanas Redshift Survey (LCRS). The distortions in (, ) shown in Figure 4 are roughly consistent with a model with = ^0.6 / b 0.5 and small-scale velocity dispersion 400 km s^-1. A similar value for emerges from the quadrupole to monopole ratio of the redshift-space distortions on large scales. As a consistency check on the results, the projected correlation function (r), derived by integrating over (, ), has been compared to that obtained by Baugh & Efstathiou (1993) from a deprojection of the angular correlation function of the parent APM galaxy catalogue. There is excellent agreement on scales up to 30 h^-1 Mpc, while on larger scales the cosmic variance dominates the uncertainties in the as-yet-incomplete 2dFGRS.

Figure 4. The 2dFGRS redshift-space correlation function, (, ), shown both as a contour plot (left) and false-colour image (right). Note the stretching/flattening along the line of sight () for small/large separations in the plane of the sky ().

In a similar vein, [Szalay] showed the results of simulations indicating the precision that the Sloan survey will achieve in recovering cosmological parameters from LSS statistics. SDSS should be able to measure the power spectrum normalization ₈ to a precision of 5%, the power spectrum shape parameter to 20%, and the redshift-distortion parameter (which involves both the mass density and the bias parameter b, = ^0.6 / b) to 35%. The precision with which P(k) will be determined is illustrated in Figure 5, which shows both the effective window functions of various surveys and the simulated recovery of P(k) from the Sloan survey, with estimated errors.

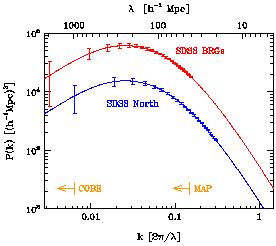
Figure 5. (a) The window function functions for various surveys: lower left is QDOT, upper left is CfA2, upper right is LCRS, lower right is the BEKS pencil-beam survey, and the small dot in the center is SDSS and 2dFGRS (from the SDSS Black Book). (b) The prediction for the recovered power spectrum and estimated errors from the SDSS main northern galaxy sample and from the Bright Red Galaxy sample (Loveday & Pier 1998). The scales covered by the COBE and MAP cosmic microwave background probes are also indicated.

On larger scales of both space and time, [Croom] reported preliminary LSS results for the 2dF QSO Redshift Survey. The LSS goals of the QSO survey are: (i) determining the QSO P(k) out to scales ~ 1000 h^-1 Mpc; (ii) measuring the cosmological constant from geometrical (as opposed to dynamical) distortions of clustering in redshift space; (iii) tracing the evolution of QSO clustering out to z ~ 3 to constrain and the QSO bias parameter. As with the galaxy survey, corrections are needed for the partial coverage of overlapping fields, the deficit of close pairs and Galactic extinction. Preliminary determinations of the 0.3 < z < 2.2 QSO correlation function using 2765 QSOs give 1.4 and scaling lengths r₀ 3 h^-1 Mpc and for r₀ 5 h^-1 Mpc for models with (_M = 1, = 0) and (_M = 0.3, = 0.7) respectively, with the clustering appearing to be constant in comoving coordinates over this range. With the full QSO survey it should be possible to measure to 3% and r₀ to 5% on small scales, and on large scales to measure P(k) on scales k > 0.01 h Mpc^-1 (i.e. < 600 h^-1 Mpc).

Other cosmological parameters were addressed by Mould and Peterson. [Mould] summarised the results from the HST Key Project to measure the Hubble constant, H₀ (Mould et al. 1999). This work essentially consists of using Cepheid distances to calibrate a wide variety of distance estimators, including type Ia supernovae, the Tully-Fisher relation for spiral galaxies, and the Fundamental Plane and surface brightness fluctuations for bulge-dominated galaxies. The available data from all these estimators yield consistent values for H₀, and the combined best estimate, after correcting for the chemical composition dependence of the Cepheid period-luminosity relation, is H₀ = (68 ± 6) km s^-1 Mpc^-1 (including random and systematic errors), for an assumed LMC distance of 50 ± 3 kpc. [Rowan-Robinson] also gave an estimate of the Hubble constant using a similar compilation of methods based on the Key Project Cepheid distances, but with the addition of corrections for peculiar velocities based on the PSCz flow model. He finds H₀ = (65 ± 2) km s^-1 Mpc^-1 (random error only).

[Mould] also considered the possibility that we inhabit a large local void with -0.5 < n / n < -0.2, as suggested by [Guzzo] from the results of the ESP survey, and as is consistent with the preliminary results from the 2dFGRS. Since H₀ / H₀ = 1/3 n / n this would imply (for = ^0.6 / b 0.5) that 0.92 < H₀^global / H₀^local < 0.97.

[Peterson] addressed the question of whether a cosmological constant is demanded by the galaxy number counts. He finds that the surface density of faint galaxies derived from the optical and near-infrared number counts is too high to be compatible with a _M = 1 cosmology, and are much better fitted by a low-density flat universe with 0.8. Although this claim depends on the assumed evolutionary history of the galaxies, Peterson argued that models which reproduce the number counts by invoking merger-driven evolution are inconsistent with the low measured amplitude of the angular correlation function for faint galaxies.