4.2. Source Counts

To predict the number of sources that will become available with the future sensitivity, let us adopt a simple model of starburst formation, in the frame of the hierarchical theory of galaxy formation. The cosmology adopted here is an Einstein-de Sitter model, = 1, with no cosmological constant, and H₀ = 75 km/s/Mpc, q₀ = 0.5.The number of mergers as a function of redshifts can be easily computed through the Press-Schechter formalism (Press & Schechter 1974), assuming self-similarity for the probability of dark halos merging (i.e. independent of mass, Blain & Longair 1993): the mass spectrum of bound objects is, at any redshift z:

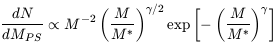
where = (3 + n) / 3, and n the power-law slope of the primordial fluctuations (n = -1 here, so that = 2/3). The turn-off mass M^* is increasing with redshift as:

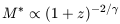
Following Blain et al. (1999c), we also write the merger rate as a function of M and z under the form:

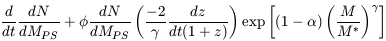
This shape (with = 1.7 and = 1.4) has been chosen so that the merger rate is the sum of the net evolution of the Press-Schechter distribution at any mass, plus a specific term, indicating that the merger probability is maximum at equal masses, and is exponentially vanishing at high mass ( cf. Blain & Longair 1993).

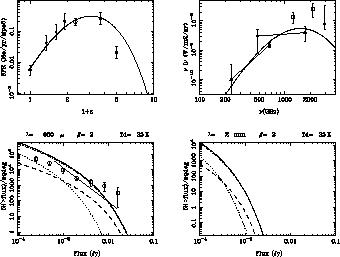
This gives the number of mergers at each epoch, but the efficiency of mergers in terms of star-formation must also vary considerably with redshift, with a peak at z ~ 2, to agree with the observations (such as in Fig. 5). Also, the integration over all redshifts of the flux of all sources should agree with the cosmic infrared background detected by COBE (Fig. 5). These contribute to reduce the number of free parameters of the modelling. To fit the source counts, however, another parameter must be introduced which measures the rate of energy released in a merger (or the life-time of the event): this rate must increase strongly with redshift (cf. Blain et al. 1999d). Once the counts are made compatible with the submm observations, the model indicates what must be the contributions of the various redshift classes to the present counts (cf. Fig. 5). It is interesting to note that the intermediate redshifts dominate the counts (2 < z < 5), if we allow the star formation to begin before z = 6. At higher dust temperature, the counts are dominated by the highest redshifts (z > 5). But these contributions depend strongly on the adopted shape of the star-forming efficiency versus z. Observations of these counts and their redshift distribution will therefore bring a lot of insight in the physiscs of early protogalaxies.

Figure 5. Top left: History of the star formation rate, adopted by the hierarchical model used here, compared with observations. The point at z = 0 is from Gallego et al. (1995), the 3 following ones (full circles) from Flores et al. (1999), the empty circle from Yan et al. (1999), and the two high redshift points (filled squares), from Pettini et al. (1998). Top right: Predictions of the model for the far-infrared cosmic background: the observations have been used to constrain the parameters of the model. The filled triangles with a line joining them symbolise the spectrum derived by Puget et al. (1996) from COBE, the filled circles are from Hauser et al. (1998), and the filled square from Dwek et al. (1998). Bottom left and right: Source counts predicted at 850 µm and 2mm respectively: the solid line is the total. Dash is the lowest redshifts (z < 2); Dot-dash, intermediate (2 < z < 5); Dots are the highest redshifts (z > 5). The emission from the dusty starbursts have been assumed a grey-body at a temperature of 35K, and an opacity varying as 2. The empty circles are data from Blain et al. (2000), and the straight line is a fit to the data derived by Barger et al. (1999a) at 850 µm.

It is possible to derive also the source counts for the CO line emission. The spectral energy distribution is now obtained with a comb-like function, representing the rotational ladder, convolved with a Planck distribution of temperature equal to the dust temperature, assuming the lines optically thick. The frequency filling factor is then proportional to the rotational number, and therefore to the redshift, for a given observed frequency. The width of the lines have been assumed to be 300km/s. The derived source numbers are shown in Fig. 6. Note how they are also dominated by the high redshift sources. It is however not useful to observe at below 1mm for high-z protogalaxies, but instead to shift towards = 1cm.

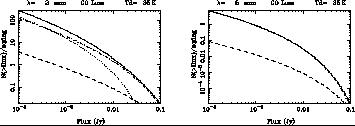
Figure 6. Left Source counts for the CO lines at an observed frequency of 2mm, assuming optically thick gas at Tex = 35K. Right Same for = 5mm. The meanings of the line styles are as in fig 5.