4.1. Orbits and resonances

First, let us recall the characteristics of orbits in an axisymmetric potential (r) in the plane z = 0. A circular orbit has an angular velocity ² = 1/r d / dr. In linearizing the potential in the neighborhood of a circular orbit, the motion of any particle can be expressed in first order by an epicyclic oscillation, of frequency ,

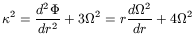
The general orbit is therefore the combination of a circle and an epicycle, or a rosette, since there is no rational relation between the two periods.

The bar creates a bisymmetric gravitational potential, with a predominant Fourier component m = 2, which rotates in the galaxy with the pattern speed _b. There is a region in the plane where the pattern speed is equal to the frequency of rotation , and where particles do not make any revolution in the rotating frame. This is the resonance of corotation (cf figure 4).

Figure 4. left: Various types of resonant orbits in a galaxy. At the ILR, the orbit is closed and elongated, and is direct in the rotating frame. At Corotation (CR), the orbit makes no turn, only an epicycle; at OLR, the orbit is closed, elongated and retrograde in the rotating frame. In between, the orbits are rosettes that do not close. right: Frequencies , - /2 and + /2 in a galaxy disk. The bar pattern speed b is indicated, defining the locations of the Linblad resonances.

In the rotating frame, the effective angular velocity of a particle is ' = - _b. There exists then regions in the galaxy where ' = /m, i. e. where the epicyclic orbits close themselves after m lobes. The corresponding stars are aligned with the perturbation and closely follow it; they interact with it always with the same sign, and resonate with it. These zones are the Lindblad resonances, sketched in Figure 4. According to the relative values of and in a realistic disk galaxy, and because the bar is a bisymmetric perturbation, the most important resonances are those for m = 2.

Periodic orbits in the bar rotating frame are orbits that close on themselves after one or more turns. Periodic orbits are the building blocks which determine the stellar distribution function, since they define families of trapped orbits around them. Trapped orbits are non-periodic, but oscillate about one periodic orbit, with a similar shape. The various families are (Contopoulos & Grosbol 1989):

• the x₁ family of periodic orbits is the main family supporting the bar. Orbits are elongated parallel to the bar, within corotation. They can look like simple ellipses, and with energy increasing, they can form a cusp, and even two loops at the extremities.

• the x₂ family exists only between the two inner Lindblad resonances (ILR), when they exist. They are more round, and elongated perpendicular to the bar. Even when there exist two ILRs in the axisymmetric sense, the existence of the x₂ family is not certain. When the bar is strong enough, the x₂ orbits disappear. The bar strength necessary to eliminate the x₂ family depends on the pattern speed _b: the lower this speed, the stronger the bar must be.

• Outside corotation, the 2/1 orbits (which close after one turn and two epicycles) are run in the retrograde sense in the rotating frame; they are perpendicular to the bar inside the outer Lindblad resonance (OLR), and parallel to the bar slightly outside.