5.1. Physical nature of instabilities
The density wave theory has been developped in the WKBJ (kr
>> 1 approximation)
and linear regime (e.g.
Lin & Shu 1964,
Toomre 1977).
The amplification of
the waves occurs at corotation, since the energy and angular momentum
of the perturbation are positive outside and negative inside corotation.
Waves are partially transmitted, and partially reflected at corotation, which
is a zone of evanescence for the waves if Q > 1.
The wave transmitted will carry energy and angular momentum of
opposite sign of the incident wave:
for conservation, the reflected wave must have
increased amplitude. Waves can spontaneously develop if the
corotation amplifier is coupled to a
reflection at a resonance or boundary (turning
point). The feedback cycle may be the WASER
(Mark 1974)
or the SWING
(Toomre 1977).
The turning points are located at the radii when
p = (
±
/ m) (1 -
1/Q2)1/2.
For m = 1 perturbations, there cannot exist ILR and OLR at the same time (see fig 16). For lopsided instabilities, developping around a central mass in a nearly-keplerian disk, there exists another amplifier, which releases the need of corotation: the indirect potential, which is due to the off- centring of the central mass (Adams et al 1989, Shu et al 1990).
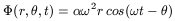
This indirect potential creates in permanence a long-range force.
The disk behaves like a resonant cavity
with the off-centring constantly stimulating new
long trailing waves.
The central mass gains angular momentum, and the disk also
outside corotation: this is not in contradiction, since in
fact in a frame centered on the central mass, the angular momentum of
the disk is of opposite sign (with respect to that
centered on the system center of mass).
While the growth rate of the mode
must be
~ for the SWING
mechanism, here
<<
.
This mode allows the inner disk to lose angular momentum,
and to inflow on the central mass.
|
|
Figure 16. left: Pattern of lopsided
ellipsoidal orbits forming a one-arm leading spiral.
right: Frequencies |