8.1. Black hole growth and activity life-time

It is widely believed that AGN derive their power from supermassive black holes, but their formation history, their demography, their activity time-scales are still debated. The two extreme hypotheses have been explored: either only a small percentage of galaxies become quasars, and they are continuously fueled, and active over Gyrs, or a massive black hole exists in almost every galaxy, but they have active periods of only a few 10⁷ yr. In the first hypothesis, there should exist blak holes with masses 100 times higher than the maximum observed today, and accretion rates much lower than the Eddington rate, and this is not supported (e.g. Cavaliere & Padovani 1989). Models with a duty cycle of 4 10⁷ yr are favored, and many galaxies today should host a starving black hole (Haehnelt & Rees 1993).

The density of black holes derived today from the kinematics of galaxy centers at high spatial resolution (Magorrian et al. 1998, Ferrarese & Merritt 2000) strongly constrains the duty cycle time-scale. Also the cosmic background radiation detected at many wavelengths constrains the formation history. The volumic density of massive black holes today _bh can be expressed as a function of the density of the bulges _bul (normalized to the critical density to close the universe), and of the observed ratio between black-hole and bulge mass M_bh / M_bul:

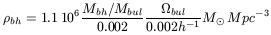
with h the usual ratio of the Hubble constant to 100 km/s/Mpc (Haehnelt et al. 1998). It is interesting to note that this ratio largely exceeds (by a factor 10) the mass density in black holes needed to explain the blue light purely by accretion on AGNs:

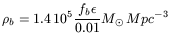
where f_b is the fraction of light emitted in blue, and the mass-to-energy conversion efficiency (section 2). This might be interpreted as a strong extinction of the blue light from AGNs, since part of the energy then can be seen in the infrared light. From the detected cosmic infrared radiation, and assuming that about 30% is coming from AGN (e.g. Genzel et al 1998), the predicted density is:

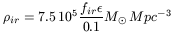
Part of the radiation is also observed through hard X-rays, and from the background hard-Xray radiation, the corresponding black hole density would be:

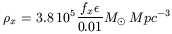
Note however that the sources contributing to the submillimetric and hard-Xray backgrounds are not the same, as discovered recently with Chandra (Severgnini et al. 2000). This could mean that even the hard-Xrays are extincted and most of the AGN radiation comes essentially in the infrared.

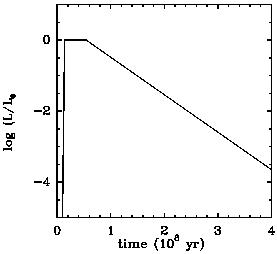
The best interpretation of the observations lead to an AGN activity life-time of ~ 4 10⁷ yr. During this time the AGN would accrete and radiate at the Eddington limit. Before, the black hole is not massive enough to accrete efficiently, since the Eddington limit is proportional to its mass. The external fueling rate is larger than the limit during the growth phase, then during its bright phase of ~ 4 10⁷ yr the AGN radiates the most efficiently at Eddington luminosity, until the fuel is exhausted, and the AGN fades away (see fig 24).

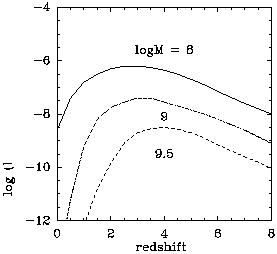
Figure 24. left A schematic view of the activity phase of a typical quasar: during the growth phase, the AGN does not radiate efficiently, although the fueling rate is larger than Eddington. After its luminous phase of ~ 4 107 yr, the fuel is exhausted and the AGN fades away. right The black hole formation rate, or number density of newly formed BH per comoving volume, per time, and lnM, in Mpc-3 (107yr)-1 (lnM)-1 (from Haehnelt & Rees 1993).

In CDM hierarchical scenarios, the smallest halos form first, and they are denser, since the density of the Universe is a strong increasing function of redshift. Then the dynamical time-scale in such structures are much shorter. Due also to a higher gas mass fraction at high redshift (not yet consumed in stars), there are many reasons why the mass of the black holes formed are higher at high redshift (even if they form in smaller-mass systems). This can explain the density distribution and luminosity function observed for quasars (cf Boyle et al 1991): at high z, the quasars were both more numerous and their black holes more massive (assuming that we all see them in their bright phase, at Eddington luminosity).

To take into account these arguments, and reproduce the fact that the more massive black holes form in the smaller haloes, Haenelt & Rees (1993) assume the ratio:

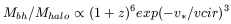
the dependence in (1+z) corresponds to the higher efficiency to form a black hole at high z (due to the high densities), the exponential cut-off for low v_cir takes into account the difficulty of small mass system to retain gravitationnally their gas in their small potential well (v_* is a normalizing value). With this model, the result is indeed that at low redshift, mostly small black holes are built, while the peak of formation of very massive black holes occurs at z = 4 (see fig 24).

Today, merging of galaxies create a quasar in only small-mass gaseous objects. If the black hole formation process is not efficient at low redshift, the main process creating AGNs now is the tidally triggered nuclear activity, through gas accretion and minor mergers. To explain for instance the 1% of Seyferts in field galaxies (Huchra & Burg 1992), it is sufficient to assume a duty cycle of 1% of "normal" galaxies.

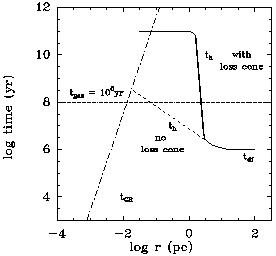
Figure 25. Time-scales relevant to the formation of a black-hole binary, in the merger remnant of two galaxies. Dynamical friction in the core of the elliptical galaxy formed, is acting in tdf ~ 106 yr. Within rh, the evolution will proceed on th = (rh / r)tdf if loss-cone effects are neglected. However, taking into account depletion of stars in the loss cone leads to th = 1011 yr, a much longer time. If infall of gas is considered, tgas ~ 108 yr applies. At the end, gravitational radiation will take over (tGR); from Begelman et al (1980). The core radius rc, the ``bound'' radius rb, the hardening radius rh and the loss-cone radius rlc are defined in the text.