Annu. Rev. Astron. Astrophys. 1992. 30: 575-611 Copyright © 1992 by Annual Reviews. All rights reserved

6.2 A Simple Model for Radio Emission from Normal Galaxies

The global radio nonthermal and thermal luminosities plus the FIR/radio ratio for most normal galaxies can be approximated by a simple model with only one free parameter, the average formation rate of stars more massive than 5 M:

The ``extended'' Miller-Scalo (1979) IMF (M) M^-5/2 is truncated at M_U ~ 100 M. All stars more massive than M_SN = 8 M become radio supernovae, so the radio supernova rate _SN is determined directly by the star-formation rate:

The nonthermal luminosity L_N can then be obtained from Equation 18; it is

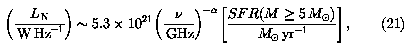
where ~ 0.8 is the nonthermal spectral index.

The radio thermal fraction can be estimated from stellar models for an assumed electron temperature T_e ~ 10⁴ K if dust absorption of Lyman continuum photons is negligible. The results of Kennicutt (1983a) imply

Then Equations 2, 3, and 4 yield

The thermal fraction implied by the ratio of Equations 21 and 23 agrees well with the average observed value (Equation 5). The ionization rate is

Blue luminosity is a poor quantitative measure of very recent (< 10⁸ yr) star formation because of extinction in molecular clouds plus confusion by older (up to 10⁹ yr) unobscured stellar populations of blue stars (Sage & Solomon 1989). Massive stars are formed in dusty giant molecular clouds from which only a small fraction of the UV or even optical (e.g. H) photons actually escape, so that nearly all of the luminosity produced by stars in H II regions emerges in the FIR. For typical dust temperatures and emissivities, about 2/3 of this emission appears in the FIR band between ~ 40 µm and 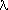~ 120 µm (Helou et al. 1988). Conversely, most of the luminosity in the band measured by FIR is from dust heated by stars more massive than M ~ 5 M (Devereux & Young 1990, Xu 1990). For a time-independent IMF

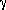where (M) is the lifetime of a star with mass M and L(M) is its average bolometric luminosity. The total energy L(M)(M) emitted by a massive star during its main-sequence life (Maeder 1987) can be approximated by L ~ 10^9.6 (M / M)^3/2 L yr. If the IMF slope is ~ 2.5 for M 5 M, then each logarithmic stellar mass range contributes equally to L_FIR and

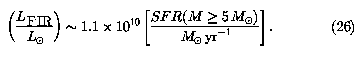
Both L_N + L_T and L_FIR are proportional to the star-formation rate, so this model implies a linear FIR/radio correlation. The FIR/radio ratio at ~ 1.4 GHz predicted by Equations 21, 23, and 26 is q ~ 2.4, close to the average observed value < q > ~ 2.3 for moderately luminous (L_FIR 10⁹ L) galaxies (Condon et al. 1991a). Also, the ratio L(H) / L_FIR ~ 0.01 from Equations 22 and 26 is in reasonable agreement with the data in Devereux & Young (1990).

Since SRF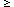(M 5 M) is the only free parameter, only one observable (e.g. the radio luminosity at one frequency) per galaxy is needed to determine its model parameters. For example, the measured radio luminosity of M82 is L_N + L_T ~ 1.0 x 10²² W Hz^-1 at = 1.4 GHz. The ratio L_N / L_T ~ 8 follows from either Equation 5 or the ratio of Equations 21 and 23. The model then predicts the star-formation rate SFR(M 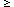5 M) ~ 2.2 M yr^-1, the radio supernova rate _SN ~ 0.1 yr^-1, the ionization rate N_uv ~ 8 x 10⁵³ s^-1, and the FIR luminosity L_FIR ~ 2.4 x 10¹⁰ L. These values are all in very good agreement with the data.

The relative contributions to _SN 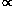L_N, L_FIR, and N_uv 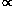L_T from stars in different ranges of log(M / M) are plotted for this model in Figure 9. Since the range of stellar masses contributing most to _SN falls within the broad range of masses producing L_FIR, the FIR/radio ratio should be relatively insensitive to time variability or slope changes in the assumed IMF. The thermal fraction L_T / (L_N + L_T) is less robust because there is less overlap between the stellar mass ranges responsible for supernovae and ionization. The steady-state models of Leitherer (1990) indicate that a change 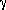in the IMF slope changes the log of the thermal fraction by approximately - 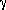/ 2. About 3 x 10⁶ yr after the termination of a starburst, the ionization rate (Leitherer 1990) and hence the thermal luminosity fall precipitously while the supernova rate and nonthermal emission persist. Thus, it is unlikely that the sharp spectral cutoff at ~ 8 GHz reported for NGC 1569 is a consequence of relativistic electron energy losses in a post-starburst galaxy (Israel & de Bruyn 1988) since NGC 1569 still has a normal thermal fraction.

Figure 9. The relative contributions to the supernova rate _SN, the far-infrared luminosity L_FIR, and the ionization rate N_uv (the last from Leitherer 1990) per logarithmic interval of stellar mass for a time-independent IMF 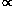M^-5/2 truncated at M_U = 100 M. Abscissa: log stellar mass in solar mass units. Ordinate: relative contribution per logarithmic mass range.