Copyright © 1994 by Annual Reviews. All rights reserved
|
Annu. Rev. Astron. Astrophys. 1994. 32:
371-418 Copyright © 1994 by Annual Reviews. All rights reserved |
This section provides a brief account of the standard theory of GI, and
of the linear and quasi-linear approximations which serve the analysis
of motions. Let x, v, and 
g be the position, peculiar velocity and
peculiar gravitational potential in comoving distance units,
corresponding to ax, av, and
a2 g in physical units, with a (t) the universal
expansion factor. Let the mass-density fluctuation be
(
- bar) / . The equations
governing the evolution of fluctuations of a
pressureless gravitating fluid in a standard cosmological background
during the matter era are the Continuity equation,
the Euler equation of motion, and the Poisson field
equation (e.g. Peebles 1980;
1993):
with H and
In the linear approximation,
the GI equations can be combined into a time evolution equation,
The use of
A basis for useful quasi-linear relations is provided by the
Zel'dovich (1970)
approximation. The displacements of particles
from their initial, Lagrangian positions q to their Eulerian positions
x at time t are assumed to have a universal time dependence,
For the purpose of approximating
GI, the Lagrangian Zel'dovich approximation can be interpreted in
Eulerian space, q(x) = x -
f-1 v(x), provided that
the flow is laminar (i.e., that multi-streams are appropriately
smoothed over). The
solution of the continuity equation then yields
(Nusser et al. 1991)
where the bars denote the Jacobian determinant, and I is the
unit matrix. The Zel'dovich displacement is first order in
f-1 and
v, so
A modified approximation, which is derived by adding a second-order term
to the Zel'dovich displacement
(Moutarde et al. 1991)
and truncating all
the expressions at second order while solving the continuity equation,
is (Gramman 1993a)
The factor 4 / 7 replaces 1 in the second-order term of
Since the variance of
Because the first two terms vanish when integrated over
a large volume, the moments
Figure 1 demonstrates the accuracy of the
explicit quasi-linear
approximations using CDM N-body simulations and 12 h-1Mpc
smoothing
(Mancinelli et al. 1994).
dot + 
· v + · (v ) = 0,
)v = - 
g ,
2 g =
(3/2)H2 
,
varying in time. The dynamics do not depend on the value of the Hubble
constant H; it is set to unity by measuring distances in km
s-1 (1h-1Mpc = 100 km s-1).
dotdot + 2H dot =
(3/2)H2 .
The growing mode of the solution, D (t),
is irrotational and can be expressed in terms of
f() H-1
Ddot / D 
0.6
(see Peebles 1993,
eq. 5.120). The linear relation between density and velocity is
= 0 -(Hf)-1
· v.
0
is limited to the small dynamical range between a few
tens of megaparsecs
and the ~ 100 h-1Mpc extent of the current samples. In
contrast, the sampling of galaxies enables reliable dynamical analysis
with smoothing as small as ~ 10 h-1Mpc, where
| · v|
obtains values 
1 so
quasi-linear effects play a role.
Unlike the strong non-linear effects in virialized
systems which erase any memory of the initial conditions, mild non-linear
effects carry crucial information about the formation of LSS, and should
therefore be treated carefully.
Figure 1 shows that 0 becomes a severe underestimate at large
||.
This explains why Equation (4) is invalid in the
non-linear epoch even where = 0 ; the requirements that
d3 x
= 0 by definition and
· v
d3 x = 0 by isotropy imply
- · v >
at || << 1.
Fortunately, the small variance of · v given
promises that some function of the velocity derivatives may be a
good local approximation to .
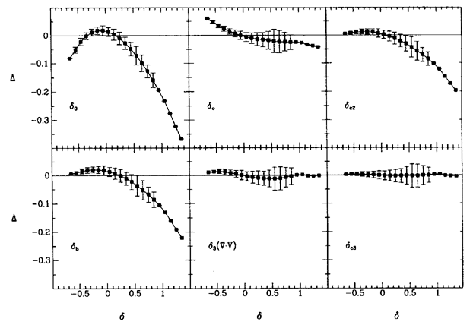
Figure 1. Quasi-linear velocity-to-density approximations.
approx(v) -
true. The mean
and standard deviation are from large standard-CDM N-body
simulations normalized to
8 = 1,
Gaussian-smoothed with radius 12 h-1Mpc (see
Mancinelli et al.
1994). Note the factor of 5 difference in scale between the
axes.
(q) =
f-1 v(q, t).
c(x) =
|| I - f-1 ð v / ð x|| -
1,
c involves second- and third-order terms (mv2,
mv3) as well. The relation (6) is not easily
invertible to provide
· v or
v when is given, but
a useful approximation derived from simulations is · v =
-f / (1 +
0.18).
c2 =
-f-1
· v + (4 / 7)f-2
m v2 ,
i j > i
(ði vi
ðj vj
-
ðj vi ði
vj).
c. While
terms are kept to second-order, it is still not an
exact solution to the second-order equations of GI. This relation can be
inverted in second-order to provide · v given , with mv2
replaced by an analogous expression mg2, involving the
gravitational acceleration g.
given · v
is small, one expects that a non-linear function of · v which
properly corrects for
the systematic deviation can be a good quasi-linear approximation to
(and vice versa).
Assuming Gaussian initial fluctuations,
Bernardeau (1992) found a
solution in the limit of vanishing variance:
b = [1 -
(2 / 3)f-1
· v]3/2 - 1, which is
easily invertible. A polynomial expansion with non-vanishing variance
should have the form (Zehavi & Dekel, in preparation)
n ( · v) =
-f-1
· v +
a2 f-2[( ·
v)2 - µ2]
· v)3 -
µ3] + . . .
<( ·
v)n> 0.3 and
a3 -0.1,
tested for values 0.1-1
and smoothing radii 5-12 h-1Mpc at 8 = 1 (8 is the rms of
unsmoothed
mass- in top-hat spheres
of radius 8 h-1Mpc).
The structure of Equation (8) makes it
robust to uncertain features such as , the shape
of the fluctuation power spectrum, and the degree of non-linearity
as determined by the fluctuation amplitude and the smoothing.
Such robustness is crucial when using a quasilinear
approximation for determining , for example (Section 8).
c, of scatter ~ 0.1,
is an excellent approximation for 
1 but it is a slight
overestimate at the negative tail. c2 and b do better
at the negative tail, but they are severe underestimates in the positive
tail. 3( · v) is an
excellent robust fit over the whole
quasi-linear regime.
c3 is constructed from the three terms in
the expansion of c
in powers of f-1
but with the numerical coefficients
adjusted to achieve best fit in the simulation (-1.05, 0.9, 1.5
replacing unity, independent of ).