


2.5. The Age of the Universe
Measured independent lower bounds on the Hubble constant and on the age
of the oldest globular clusters provide a lower bound on
H0t0
(= 1.05ht, where H0
 100h km
s-1Mpc-1 and
t0
100h km
s-1Mpc-1 and
t0  10tGyr),
and thus an interesting constraint in the
10tGyr),
and thus an interesting constraint in the
 m -
m -

 plane.
The exact expressions are computable in the various regions of
parameter space. For example, for
plane.
The exact expressions are computable in the various regions of
parameter space. For example, for

 = 0, the relation is
(e.g.,
[15], Eq. 2.79)
= 0, the relation is
(e.g.,
[15], Eq. 2.79)
where
C+1-1
where S
New Developments:
Progress is being made in the HST key project to measure
H0 based on Cepheids in Virgo and Fornax.
Pro:
The method does not depend on fluctuations, GI, biasing, etc.
Con:
The errors in the determination of the age of the universe based on
globular clusters are uncertain. The major source of error are the
distances to Pop-II stars in the globular clusters, and
complex stellar evolution issues.
Current Results:
The most likely estimates are of
h
Figure 1 displays in the
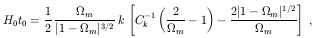
 cos-1 and
C-1-1
cos-1 and
C-1-1
 cosh-1.
A very useful approximation in the presence of a cosmological constant,
that is an exact solution for a flat universe, is
[1]
cosh-1.
A very useful approximation in the presence of a cosmological constant,
that is an exact solution for a flat universe, is
[1]
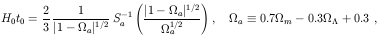
 a
a
 1-1
1-1
 sinh-1
and
S
sinh-1
and
S a >
1-1
a >
1-1  sin-1. A useful crude approximation near
H0t0 ~ 2/3 is
sin-1. A useful crude approximation near
H0t0 ~ 2/3 is
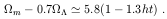
 The current error of ~ 20% in the Hubble constant
will hopefully be reduced soon to the level of 10% percent.
The current error of ~ 20% in the Hubble constant
will hopefully be reduced soon to the level of 10% percent.
 This method is likely to provide the most stringent upper bound on
This method is likely to provide the most stringent upper bound on
 m and lower bound on
m and lower bound on

 .
.
 0.6 - 0.7
[16]
and
t
0.6 - 0.7
[16]
and
t  1.5
[17],
corresponding to ht
1.5
[17],
corresponding to ht  1. They seem to favor a possible
deviation from the Einstein deSitter model towards low
1. They seem to favor a possible
deviation from the Einstein deSitter model towards low
 m
or high
m
or high

 or both.
However, one only needs to appeal to the current
~ 1
or both.
However, one only needs to appeal to the current
~ 1 lower bounds
(say
h
lower bounds
(say
h  0.53 and
t
0.53 and
t  1.2)
in order to accommodate the Einstein deSitter model.
1.2)
in order to accommodate the Einstein deSitter model.
 m-
m-

 plane the ~ two-sigma
constraints from the global measures discussed above.
Superposed is the main constraint from cosmic flows
(Section 4 below).
The joint permitted range for
plane the ~ two-sigma
constraints from the global measures discussed above.
Superposed is the main constraint from cosmic flows
(Section 4 below).
The joint permitted range for
 m is thus roughly
0.4 to 1.1. Low
m is thus roughly
0.4 to 1.1. Low  m
models of
m
models of
 m
m
 0.3 are significantly ruled out.
0.3 are significantly ruled out.