


Flux limited radio source catalogs are dominated by elliptical
galaxies with high luminosities [ (L) peaks at L ~ 1025.5 W Hz-1] at
very large distances (median z ~ 1). This is because the present
luminosity function is quite flat; it is roughly fit by two power
laws:
(L) peaks at L ~ 1025.5 W Hz-1] at
very large distances (median z ~ 1). This is because the present
luminosity function is quite flat; it is roughly fit by two power
laws:
Above L
Above L
with
To study the radio luminosity function of normal galaxies in the
present epoch requires that we sift through a large sample of radio
sources, selecting those few associated with optically bright, nearby
galaxies. This preselection by optical properties causes a bias for
optically brighter objects. To properly include this selection in a
statistical treatment requires computation of the bivariate radio
luminosity function (BRLF), f(P, M), which gives the fraction of all
galaxies with optical magnitudes M to M + dM which have radio luminosity
P to P + dP
(Auriemma et al. 1977,
Hummel et al. 1983).
A simpler
approach is to compute the radio-optical ratio function, RORF, given
by f(R), the fraction of galaxies with radio-optical luminosity ratio
in the range R to R + dR, where R is commonly defined as
(Condon 1980).
Either of these functions can be written as a
differential function, f(R), or integral (cumulative) function
F>(R).
Results for f(R) are summarized by
Gavazzi and Jaffe
(1986),
who find a log-normal distribution for f(R), with mean value
R0 = 10 for Sc's and R0 = 25 for Sb's, and width 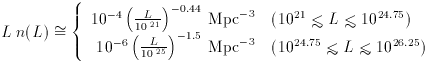
 2 x 1026 W
Hz-1 it drops off. Evolution of the luminosity
function is critical in determining the observed n(s), as discussed by
Condon (1984a).
Spiral galaxies make up a small fraction (~ 1%) of the
radio sources brighter than 1 mJy. Typical spirals detected at this
level are nearby, because for these
2 x 1026 W
Hz-1 it drops off. Evolution of the luminosity
function is critical in determining the observed n(s), as discussed by
Condon (1984a).
Spiral galaxies make up a small fraction (~ 1%) of the
radio sources brighter than 1 mJy. Typical spirals detected at this
level are nearby, because for these  (L) peaks near 1021 W Hz-1. The
luminosity function for spirals is given by
(Condon 1984b):
(L) peaks near 1021 W Hz-1. The
luminosity function for spirals is given by
(Condon 1984b):
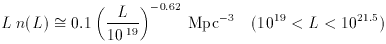
 1021.5 watt
Hz-1 the density of spirals drops off, and
ellipticals dominate. An alternative form suggested by Hummel
(1981,
cf. Gavazzi and Jaffe
1986)
is a log-normal luminosity function:
1021.5 watt
Hz-1 the density of spirals drops off, and
ellipticals dominate. An alternative form suggested by Hummel
(1981,
cf. Gavazzi and Jaffe
1986)
is a log-normal luminosity function:
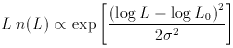
 = 0.67. L0,
the mean luminosity, is roughly proportional to
optical luminosity, with L0
= 0.67. L0,
the mean luminosity, is roughly proportional to
optical luminosity, with L0  1021 watt Hz-1 for Mp
1021 watt Hz-1 for Mp  -20.
-20.
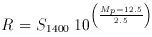
 = 0.67 in log R, i.e., a factor
of five in R.
= 0.67 in log R, i.e., a factor
of five in R.