


Traditionally faint galaxies were studied in order to constrain
the cosmological world model
([Sandage 1961]);
their evolution
was considered just one more tedious correction (the so-called
evolutionary correction) in the path to the Holy
Grail of the deceleration parameter q0
(
 M / 2 in
M / 2 in
 = 0 Friedmann models). The
most useful galaxies in this
respect were giant ellipticals in rich clusters.
Tinsley (1976)
demonstrated how sensitive the derived q0 was to the assumed
main sequence brightening with look-back time in these populations.
= 0 Friedmann models). The
most useful galaxies in this
respect were giant ellipticals in rich clusters.
Tinsley (1976)
demonstrated how sensitive the derived q0 was to the assumed
main sequence brightening with look-back time in these populations.
The traditional view for the formation history of an elliptical
followed
Eggen,
Lynden-Bell & Sandage (1962).
Monolithic collapse and
rapid star formation leads to a subsequent track known as `passive
evolution' (i.e. without further star formation). Tinsley showed that
main sequence brightening in such a stellar population is largely
governed by the rate at which stars evolve off the main sequence, i.e.
the slope x ( 1) of the
initial mass function at the typical
turnoff mass 0.4-1
M
1) of the
initial mass function at the typical
turnoff mass 0.4-1
M . Whence:
. Whence:
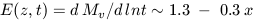
| (2.1) |
and, in terms of its bias on q0:
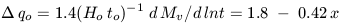
| (2.2) |
Tinsley argued that one would have to know the evolutionary
correction to remarkable precision get a secure value of
q0. In
fact, noting that the difference in apparent magnitude for a
standard candle at z = 1 between an empty and Einstein-de Sitter
Universe is only  0.5 mag, the
relative importance of cosmology and evolution can be readily gauged.
0.5 mag, the
relative importance of cosmology and evolution can be readily gauged.
Despite the above, it is always a mystery to me why several of our most eminent astronomers ([Kristian et al 1978, Gunn & Oke 1975]) continued to pursue the Hubble diagram as a cosmological probe using first-ranked cluster galaxies, in some cases for several years after the challenge of resolving the evolutionary correction became known. Tammann (1985) estimated about 400 nights nights of Palomar 200-inch time was consumed by the two competing groups whose resulting values of q0 fundamentally disagreed. Recently Aragón-Salamanca (1998) showed, in a elegant summary of the situation, how the modern K-band Hubble diagram is most likely complicated further by the fact that first-ranked cluster galaxies are still assembling their stars over the redshift interval 0 < z < 1, offsetting the main sequence brightening (Figure 2).
|
Figure 2. A recent appraisal of the prospects of
securing cosmological constraints from the Hubble diagram of
brightest cluster galaxies
([Aragón-Salamanca et al 1998]). Luminosity
evolution is
parameterised as L = L(0)(1 + z) |
In the late 1970's therefore, the motivation for studying faint galaxies became one of understanding their history rather than using them as tracers of the cosmic expansion (see inset panel in Figure 1). This is not to say that uncertainties in the cosmological model do not affect the conclusions drawn. The connection between cosmology and source evolutions remains strong in three respects:
 M universe
and consequently evolutionary trends
are much stronger in such models.
M universe
and consequently evolutionary trends
are much stronger in such models.
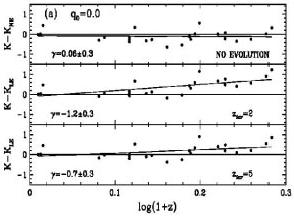
|
Figure 3. The abundance of massive
(>1011
M |
Fortunately, we are making excellent progress in constraining the cosmological parameters from independent methods, the most prominent of which include the angular fluctuation spectrum in the microwave background ([de Bernardis et al 2000, Balbi et al 2000]), the Hubble diagram of distant Type Ia supernovae ([Garnavich et al 1998, Perlmutter et al 1999]), the abundance of rich clusters at various epochs ([Bahcall & Fan 1998]) and the redshift-space distortion in large redshift surveys such as 2dF ([Peacock et al 2000]).
Given it matters, how then should we respond to the widely-accepted
concordance in the determination of
H0,  M,
M,
 from various probes
(Ostriker
& Steinhardt 1995,
Bahcall 1999)?
The claimed convergence on the value of Hubble's constant
([Mould et al
2000])
is not
so important for the discussion below since most evolutionary tests are
primarily concerned with relative comparisons at various
look-back times where H0 cancels. The most bewildering
aspect of the concordance picture is the resurrection of a non-zero
from various probes
(Ostriker
& Steinhardt 1995,
Bahcall 1999)?
The claimed convergence on the value of Hubble's constant
([Mould et al
2000])
is not
so important for the discussion below since most evolutionary tests are
primarily concerned with relative comparisons at various
look-back times where H0 cancels. The most bewildering
aspect of the concordance picture is the resurrection of a non-zero
 , the
evidence for which comes primarily from the Hubble diagram for Type Ia
supernovae.
, the
evidence for which comes primarily from the Hubble diagram for Type Ia
supernovae.
As a member of the Supernova Cosmology Project
([Perlmutter et al 1999])
I obviously take the supernova results seriously! However, this
does not prevent me from being surprised as to the implications of
a non-zero  . The most
astonishing fact is how readily the
community has apparently accepted the resurrection of
. The most
astonishing fact is how readily the
community has apparently accepted the resurrection of
 -
a term for which there is no satisfactory physical explanation
(c.f [Wang et al
2000]).
To one poorly-understand component of the
cosmic energy density (non-baryonic dark matter), we seem to have
added another (vacuum energy). It seems a remarkable
coincidence that all three significant constituents
(
-
a term for which there is no satisfactory physical explanation
(c.f [Wang et al
2000]).
To one poorly-understand component of the
cosmic energy density (non-baryonic dark matter), we seem to have
added another (vacuum energy). It seems a remarkable
coincidence that all three significant constituents
( B,
B,
 DM,
DM,

 ) are comparable in
magnitude to
within a factor of 10, and hardly a step forward that only one
is physically understood!
) are comparable in
magnitude to
within a factor of 10, and hardly a step forward that only one
is physically understood!
The lesson I think we should draw from the cosmic concordance is similar to the comment I made in Section 1 when we discussed some theorists' triumphant reconciliation of their theories with faint galaxy data (a point we will debate in detail in Section 3). In both cases, the hypothesis certainly reproduces a wide range of observations but note it takes, as input, parameters for which there is not yet a clear physical model. One should not, therefore, regard a concordant picture as anything other than one of many possible working hypotheses. In the case of the cosmological models, we need to invest effort into understanding the physical nature of dark matter and vacuum energy. In the case of galaxy evolution our goal should be to test the basic ingredients of hierarchical galaxy formation.