Copyright © 1982 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1982. 20:
547-85 Copyright © 1982 by Annual Reviews. All rights reserved |
1.2 Cluster Dynamical Evolution
In this article we assume that the differences between regular and irregular clusters can be described in an evolutionary framework. Abell (1975) characterized regular clusters as having marked spherical symmetry, a high central concentration, a galaxy population dominated by S0s and ellipticals, little (if any) subclustering, a high velocity dispersion (~ 1000 km s-1), and a large number of member galaxies (~ 1000 or more galaxies within 7 mag of the brightest galaxy). At the other extreme are the irregular clusters characterized by little spherical symmetry, an absence of central condensation, a galaxy population containing all types, significant subclustering, a lower velocity dispersion, and fewer member galaxies. In this evolutionary scenario as the cluster collapses, galactic halos are stripped, central galaxies cannibalize their neighbors, the velocity dispersion increases, and the X-ray gas is heated and its luminosity increases. Although future observations and theoretical calculations may modify or invalidate some of the details, this framework allows us to synthesize the increasing wealth of observational material into a coherent structure, permitting the comparison of many cluster properties.
The evolutionary sequence of clusters is delineated by cluster properties that can be related to processes occurring during the collapse and relaxation of a cluster - violent relaxation, equipartition, galaxy collisions, and dynamical friction. However, since the timescales for these processes depend on different parameters, they will not necessarily all behave in the same way from cluster to cluster. Therefore the evolutionary sequence should not be interpreted as one in which younger clusters become the precise replicas of evolved ones.
The timescales for the processes occurring during the dynamical relaxation of a cluster are interrelated (see Lightman & Shapiro 1978, Bahcall 1977a, and Ostriker 1978). The shortest cluster timescale is that for the violent relaxation. On this timescale, gross departures from equilibrium in the cluster potential will be reduced and the galaxies in the core will exhibit a Maxwellian distribution with little equipartition. This timescale is approximately the crossing time
where R is the cluster radius, V the velocity dispersion,
G the gravitational constant, and
where M is the mass of a galaxy, n the galaxy density, and
N the total
number of galaxies in the cluster. For typical values of the parameters
where VR is the radial component of the velocity
dispersion and Mgal is
the mass of a galaxy. The dynamical and two-body timescales are related by
Therefore for a given mean density, poorer clusters have shorter
two-body relaxation times than rich clusters.
The equipartition and dynamical friction timescales are related to
the relaxation time by
Some cluster evolutionary indicators are tied directly to dynamical
processes. For example, the increases in central galaxy density and
X-ray luminosity are related to the deepening of the gravitational
potential during the cluster collapse and relaxation. With regard to
galactic content as an evolutionary indicator,
Dressler (1980a)
argued that the cluster population depends not only on changes that occur
during the cluster's evolution (e.g., ram-pressure stripping and
evaporation) but also on the fact that S0s are born preferentially in
denser regions. However, since denser regions have shorter dynamical
timescales, regions dominated by S0s would tend to have undergone more
relaxation. In this sense, spiral fraction remains an evolutionary
indicator, although galaxy density is probably a more fundamental
parameter.
The X-ray morphology shown by imaging observations has been related
to the evolutionary sequence of clusters. Irregular, clumped emission
is associated with dynamically young (irregular) clusters
(Jones et al. 1979,
Bechtold et al. 1983).
Smooth, symmetrical emission is observed in relaxed (regular) clusters
(Jones et al. 1979,
Helfand et al. 1980),
while a possible intermediate state exhibits a biomodal
X-ray surface brightness distribution
(Forman et al. 1981a,
Henry et al. 1981).
The X-ray images also suggest that the evolutionary sequence is
divided into two parallel sequences corresponding to clusters with and
without dominant, central, galaxies. Clusters that have a core radius
of less than ~ 300 kpc have emission peaked on a central, dominant
galaxy; those with a core radius of ~ 400-700 kpc lack a central,
dominant galaxy
(Jones et al. 1979).
Although exceptions or new
families of clusters may be discovered in future analyses, the present
observations can be organized in this rudimentary system.
Figure 1
graphically illustrates this two-family classification with X-ray
isointensity contours of six clusters. The X-ray and optical dynamical
indicators span the full range for clusters in both families.
Figure 1. X-ray isointensity contours for 6
clusters from 0.5-3.0 keV
IPC images. Before contours were drawn, the images (and all other IPC
images shown in this article) were smoothed with a Gaussian (sigma =
32") whose width corresponds to that of the instrumental response. The
clusters on the left represent those from the family having large
X-ray core radii and no central, dominant galaxy. Those on the right
have smaller X-ray core radii and contain central, dominant
galaxies. The clusters at the top of the figure are less dynamically
evolved than those at the bottom. These clusters are discussed in
detail in Sections 3 and
4, and their properties are summarized in
Table 3.
X-ray observations of individual clusters from the family without
dominant galaxies (nXD) are discussed in
Section 3 beginning with the
irregular clusters Abell 1367 and Abell 194 and ending with evolved
Coma-type systems. In a parallel structure, the X-ray images of
clusters with dominant galaxies (XD) are described in
Section 4
beginning with Virgo and ending with the cD clusters and Perseus.
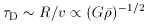
 the mean
density. Thus, clusters of high
mean density relax rapidly. The two-body relaxation timescale is
the mean
density. Thus, clusters of high
mean density relax rapidly. The two-body relaxation timescale is

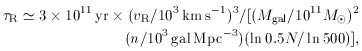
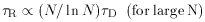
 F
F
 (
( /MH)
/MH)
 R, where
R, where
 is the mass of the
average galaxy and MH that of a heavier one. Thus, on
a timescale less
than
is the mass of the
average galaxy and MH that of a heavier one. Thus, on
a timescale less
than  R a heavy galaxy
will settle to the cluster center.
R a heavy galaxy
will settle to the cluster center.
