Adapted from P. Coles, 1999, The Routledge Critical Dictionary of the New Cosmology, Routledge Inc., New York. Reprinted with the author's permission. To order this book click here: http://www.routledge-ny.com/books.cfm?isbn=0415923549
When photons from the cosmic microwave background radiation travel through a hot plasma (with a temperature of, say, around 108 K) they collide with energetic electrons and get scattered up to X-ray energies. If we look at the cosmic microwave background radiation through such a plasma cloud, we therefore see fewer microwave photons than we would if the cloud were not there. Paradoxically, this means that the plasma cloud looks like a cool patch on the microwave sky. This photon deficiency is the essence of the Sunyaev-Zel'dovich effect, named after Rashid Alievich Sunyaev (1943 - ) and Yakov Zel'dovich.
Quantitatively, the relative temperature dip
T/T depends on the
temperature and number density of the scattering electrons
(Te and ne)
according to the formula
where the integral is taken along the line of sight through the cloud;
me is the mass of the electron, and
A particularly interesting aspect of this method is that it is
possible, at least in principle, to use it to obtain measurements of
the distance to a cluster of galaxies in a manner that is independent
of the cluster's redshift. To do this we need X-ray measurements of
the cluster (see X-ray astronomy) which give information about
ne and
Te. Comparing these with the measured
Attempts to apply this idea in practice have not been overwhelmingly
successful, rather low values being obtained for
H0. On the other
hand, it is a potentially important method because it does not rely on
the complicated overlapping series of calibrations from which the
extragalactic distance scale is usually constructed.
FURTHER READING:
Jones, M. et al., `An image of the Sunyaev-Zel'dovich Effect', Nature,
1993, 365, 320.
T/T = - 2
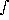(nekTe 
/
mec2) dl
is the Thomson scattering
cross-section. This effect has been detected in observations of rich
clusters of galaxies: the size of the temperature decrement
T/T is
around 10-4. Future fine-scale experiments designed to map the
fluctuations in the cosmic microwave background radiation with an
angular resolution of a few arc minutes are expected to detect large
numbers of Sunyaev-Zel'dovich contributions from individual clusters.
T/T yields an estimate of the
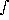total path length (L = dl) traversed by the photons on their way
through the cluster. Assuming the cluster to be spherical, or by
using a sample of clusters with random orientations, we can use L to
estimate the physical size of the cluster. Knowing its apparent
angular size on the sky then leads to an estimate of its distance;
knowing its redshift then leads to a value of the Hubble constant
H0.