4.2. Ratios Involving NV 1240

Some early studies of the permitted BELs noted that NV 1240 was significantly stronger than the predictions of photoionization models (Osmer & Smith 1976, 1977). They noted that this NV enhancement might be due to a nitrogen enhancement as discussed by Shields (1976, Section 4.1). More recently, HF93a, Ferland et al. (1996) and Hamann et al. (1997a) performed extensive analysis of the NV 1240 emission compared to CIV 1549 and HeII 1640 for estimating N/He and N/C abundances. The NV/CIV line ratio is advantageous in low signal-to-noise spectra because CIV is essentially always present. The disadvantage of this ratio is that the NV and CIV line-forming regions are not quite coincident. The NV/HeII ratio can be harder to measure because HeII is weak, but upper limits on HeII still provide useful lower limits on the N/He abundance. NV/HeII is a more robust abundance indicator because the NV emitting region lies within the He⁺⁺ zone, where HeII 1640 forms by recombination. If N⁺⁴ does not fill the He⁺⁺ zone the NV emission can be weak, but it is not possible to produce NV without also producing HeII (see also HF99 for more discussion).

We studied the theoretical NV/HeII and NV/CIV ratios for a wide variety of ionizing continuum shapes and BELR parameters. We used parameters that maximize (or nearly maximize) these ratios for comparisons to the data, so that we are most likely to underestimate the N/He and N/C abundances and thus the overall metallicity. Figure 3 compares the theoretical predictions to line ratios measured in QSOs at different redshifts. The predictions use abundances from Figure 2, a BELR density of 10¹⁰ cm^-3, an incident flux of hydrogen-ionizing photons of 10²⁰ cm^-2 s^-1, and the QSO continuum derived by Mathews and Ferland (1987; which we altered slightly to have _ox = -1.24 and an additional decline at wavelengths 1 µm). This continuum shape produces large but not quite maximum NV line ratios. See HF93a, Ferland et al. (1996) and Hamann et al. (1997a) for details on the calculations and the data set. The evolutionary ages from Figure 2 are converted to redshifts assuming the evolution begins at the Big Bang in a cosmology with _M = 1, = 0 and H₀ = 65 km s^-1 Mpc^-1. The results in Figure 3 show that the short timescales, flatter IMF (favoring high-mass stars) and higher Z's in the Giant Elliptical model provide a much better fit to the high-redshift data. Steeper IMFs (more like the Solar Neighborhood case) could account for some of the smaller line ratios if the evolution times are short enough. The largest line ratios at high redshifts could be fit by invoking BELR parameters that better optimize the NV emission or by using still-flatter IMFs.

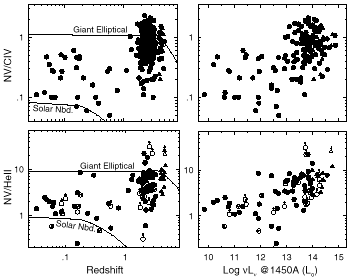
Figure 3. Observed and predicted NV/CIV and NV/HeII line ratios versus redshift (left panels) and luminosity (right panels) for a cosmology with M = 1, = 0 and H0 = 65 km s-1 Mpc-1 (see HF99).

One important empirical result is that the NV line ratios are typically larger in more luminous QSOs (HF93a, Osmer et al. 1994, Laor et al. 1995, Véron-Cetty et al. 1983). This trend could be affected by relationships between the luminosity L and various physical parameters of the BELR; however, the trend in the NV line ratios could also result entirely from higher metallicities (and higher relative N abundances) in more luminous sources (also Korista et al. 1998 and this volume). If QSO luminosities correlate positively with the masses of the QSOs and/or their host galaxies (McLeod & Rieke 1995, Magorrian et al. 1998), a metallicity-L relationship would indicate that there is a mass-metallicity relation among QSOs that is similar (or identical) to the well known relation in nearby galaxies (Section 2.2). The fact that high Z's occur only at high redshifts (Fig. 3) might result from the natural tendency to form denser or more massive systems at early epochs, when the mean density of the Universe was itself higher (Haehnelt & Rees 1993).