

The analysis of globular cluster systems (GCSs) in other galaxies is starting to fulfil its long-held promise of informing us about galaxy formation in ways that are unique. The more we learn about GCSs, the more we realize that their role in galaxy formation is an intricate and varied process - yet with common themes that apply particularly to the old-halo population that is found in every type of galaxy.
A decade ago, it was possible to write a single review article (Harris 1991) which encompassed virtually all the themes in GCS research. Today, the field has proliferated in so many directions that such a job is impossible. Instead, we will take the approach that many of the key findings about globular cluster systems have relied on the thorough study of a few critical individual galaxies of representative types. These ``case studies'' form the outline of this chapter. We have space only to touch on a few highlights: to gain a fuller idea of the richness and diversity of this field, the reader is urged to see the more comprehensive recent discussions of Ashman & Zepf (1998) and Harris (1999, hereafter denoted H99).
Our logical starting point is the globular cluster system in the
galaxy that we know best: the Milky Way. It is in many respects
a typical large spiral, and current evidence suggests that the GCSs
in other spirals like it have basically similar properties.
In global perspective, the globular clusters of the Milky Way define
a roughly spherical spatial distribution which has traditionally marked the
paradigmatic ``old halo'' of our galaxy extending out to
Rgc  40 kpc
(Figure 1).
40 kpc
(Figure 1).
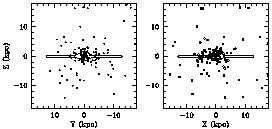
|
Figure 1. In these two projections (the YZ and XZ planes) the space distribution of the Milky Way globular clusters is seen to be approximately spherical except in the central bulge. In the XZ plane (where the Sun is at (-8, 0)), note the elongation of the inner points along the X-axis, which is largely a residual of random distance errors along the line of sight from the Sun. Note also the lack of points at large X-values along the disk beyond the Galactic center, where any ``missing'' clusters would likely be. Data for the Milky Way clusters in this and subsequent figures are taken from the catalog of Harris (1996). |
At distances beyond 40 kpc, the few remaining outermost-halo clusters join with several of the dwarf satellites of the Milky Way (Figure 2) to delineate a much larger-scale asymmetric planar distribution that may have had a distinct origin and history outside the Milky Way proper (e.g., Harris 1976; Zinn 1985; Majewski 1994; or H99).
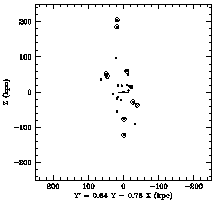
|
Figure 2. Spatial distribution of the Milky Way globular clusters (dots) more distant than 20 kpc from the Galactic center, and dwarf satellite galaxies (crosses). Most of these objects fall within a planar configuration rather than a spherically symmetric outer halo; the coordinate Y' = 0.64Y - 0.76X (where X,Y are measured relative to the Galactic center; from Majewski 1994) is chosen to show the plane ``edge-on''. |
At present, 147 globular clusters are known in the Milky Way
(Harris 1996).
Estimates of the true total population
have differed widely over the years, but most of the ``missing''
undetected ones, if any, must lie at very low Galactic latitude behind
extremely large amounts of foreground absorption. An occasional
few may lie at extremely large distances and/or small luminosities,
though only a handful of such objects have been found (usually
accidentally) over the past two decades. An analysis of these
factors by
H99
suggests that the true total is N
 160 ± 10.
160 ± 10.
The existence of two major and remarkably distinct
subpopulations in the GCS, based on metallicity and
kinematics, was suspected long ago (see especially
Kinman 1959,
with even earlier hints
in the literature) and was firmly established by the classic study of
Zinn (1985).
The metal-poor component (which I will abbreviate as MPC)
contains about 3/4 of all the clusters and is spread throughout
the halo; the metal-rich component (abbreviated MRC)
contains the remaining 1/4 of the clusters
and is almost entirely restricted to within the Solar circle,
Rgc  8
kpc. The total metallicity
distribution function (MDF) can be well described by two Gaussians
in [Fe/H] (Figure 3), and the clear
8
kpc. The total metallicity
distribution function (MDF) can be well described by two Gaussians
in [Fe/H] (Figure 3), and the clear
 1 dex separation between
the MRC and MPC groups already suggests distinct evolutionary histories
for them.
1 dex separation between
the MRC and MPC groups already suggests distinct evolutionary histories
for them.
Zinn (1985) and Armandroff (1989) interpreted the MRC as a ``disk'' population of clusters because of their high metallicity and large systemic rotation (see below), and since then it has become conventional to associate them with the old stellar thick disk or something analogous to it. Such an association, however, does not stand up entirely comfortably to the complete array of contemporary evidence. Minniti (1995) has argued persuasively that the sharply increasing space density of the MRC all the way in to the Galactic center resembles a bulge-like population far more than a disk-like one, while the net rotation of the innermost MRC clusters (see also Zinn 1996) is also like that of the old field giant stars in the Galactic bulge. The spatial distribution of the MRC is distinctly more flattened toward the Galactic plane than is the near-spherical MPC population (Zinn 1985; H99), and overall, this inner metal-rich population thus seems best associated with a flattened bulge population.
The kinematical analysis of the cluster population has drawn considerable attention in recent years, as a way of separating out possible subcomponents and thus formation histories; a group of clusters accreted, for example, from a single captured satellite galaxy such as we see happening now with the Sagittarius dwarf (Ibata et al. 1997; Da Costa & Armandroff 1995), could have distinctly different orbital properties than halo clusters formed in situ within the original potential well of the larger Galaxy. The discovery of the Sagittarius system has, in fact, stimulated numerous conjectures that the entire (metal-poor) halo might have accumulated by accretion of small satellites that were the original hosts of cluster formation.
Most of the kinematical analysis to date has necessarily relied on just the radial velocities of the clusters, although measurements of absolute proper motions and thus true three-dimensional space motions are steadily growing in reliability and importance (see below). The standard equation of condition for the radial velocity vr of a cluster relative to the Solar Local Standard of Rest is (Frenk & White 1980)
where V, V0 are the Galactic rotation
velocity vectors at the locations of the cluster and the Solar LSR;
Estimates for the mean rotation speeds and dispersions of various
subsets of clusters, broken down by metallicity and Galactocentric distance,
are summarized in Table 1 and shown in
Figures 4 and 5
(taken from the recent compilation of
H99).
Let us look first at the metal-rich component: the inner MRC clusters
(0 to 4 kpc) show a modest but clear rotation signal, consistent
with bulge rotation and with the velocity pattern of bulge
red-giant stars (see
Minniti 1995;
Zinn 1996).
On the other hand, the 4-to-9 kpc MRC group has a much
stronger rotation and lower dispersion, though still less than
the ~ 180 km s-1 characteristic of the stellar thick disk
(e.g. Majewski 1993).
Is the MRC thus a composite of bulge and thick disk?
If so, we might expect to see net age differences between them
(with the disklike ones belonging, perhaps, to a later formation epoch).
Unfortunately, no reliable differential age comparisons for these
objects are yet available, primarily because
of the very high reddenings and crowded fields in which the
inner MRC clusters are found. A clear age comparison would, however,
be of paramount importance and is very much worth pursuing.
Figure 4. Kinematical solutions for the net
rotation speeds
of the metal-rich globular clusters in the Milky Way (adapted from
Harris 1999).
Here the radial velocity of the cluster
relative to a stationary point at the LSR is plotted against
(cos
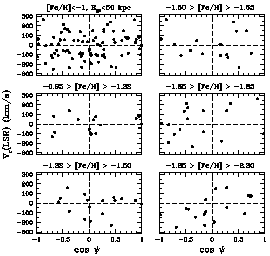
Figure 5. Kinematical solutions for the net
rotation speeds of the
metal-poor clusters in the Milky Way, excluding the four Sagittarius
member clusters and any clusters more distant than 50 kpc from
the Galactic center. The upper left panel shows all clusters combined,
while the remaining panels show the distributions for five
metallicity subgroups (see Table 1 for a similar
breakdown by Galactocentric
distance). NGC 3201, which strongly drives a ``retrograde'' solution
for V in the bin for (-1.50 > [Fe/H] > -1.65), is
the point at uppermost left in the upper right panel (see text).
The MPC (halo) clusters were, until this decade, generally thought
to be a rather homogeneous group kinematically (except possibly for
the few outermost Palomar-type clusters, which we will not discuss
in detail here). They were characterized systemically by a very modest
overall rotation (V ~ 40 km s-1), high random motion
(
In the MPC subgroups broken down
by radial zones, few significant trends emerge, all zones having
small rotation and comparably high dispersion (see
Table 1 and
H99).
However, when the sample is divided into
metallicity subgroups - which may be more closely
connected with cluster age - more significant trends do emerge.
The clearest signal is that the
most metal-poor halo component has a surprisingly significant
net rotation: the clusters with [Fe/H] < -1.7 have
V = (80 ± 43) km s-1, higher than any other MPC subgroup
and quite comparable with the innermost MRC group (see
H99).
This significant rotation is driven by the metal-poor clusters
in the inner halo (Rgc
The possibility that traces of entire accreted satellites
might be detectable kinematically - for example, by systemic retrograde
motion, if the satellite fell into the halo from a direction counter
to the normal rotation vector V - was raised by
Rodgers & Paltoglou
(1984),
who suggested that a subgroup of clusters over
a rather narrow range of [Fe/H] did indeed appear to have net
retrograde motion. This approach was later
given considerable impetus by
Zinn (1993)
and by the subsequent discovery of the Sagittarius dwarf with its
retinue of four clusters (e.g.,
Da Costa & Armandroff
1995).
These ideas are closely connected to one of the main underpinnings of the
Searle & Zinn (1978)
model in which the outer parts of the halo are envisaged as
forming from many individual dwarf-sized pregalactic fragments.
In this picture, the outer halo could reasonably be expected to
harbor globular clusters of widely different ages or kinematics,
condensing within these fragments at different times, then accreted
on many different orbital directions.
A key piece of evidence connected with this argument
is the morphological plot shown in Figure 6. If
horizontal-branch type (red, blue, or intermediate) is a reliable
indicator of cluster age, then it suggests that the outer-halo
clusters would have younger ages on average (redder HB types at
a given metallicity), as well as a larger spread in ages
(Zinn 1985,
1993).
This suggestion, however, relies strongly
on the assumption that HB morphology is driven primarily by
age at a given metallicity
(Lee et al. 1994;
Chaboyer et al. 1996).
More direct tests
must come from direct main-sequence photometry of these clusters,
which now tend not to confirm the age hypothesis (see below).
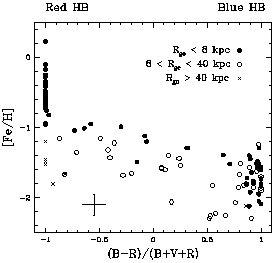
Figure 6. Globular cluster metallicity
[Fe/H] plotted against
horizontal-branch ratio (B-R)/(B+V+R) (the relative number of
blue, red, or intermediate stars on the horizontal branch;
from
Lee et al. 1994
and Harris 1996).
The HB morphology becomes progressively
redder at large Galactocentric distances. The
Zinn (1993)
``RHB'' clusters are the open circles with HB ratio less than 0.5 (see text).
To avoid prejudicing the discussion in terms of cluster age, I will
refer to these morphological groups simply as the ``red horizontal
branch'' (RHB) clusters and the ``blue horizontal branch'' (BHB) clusters.
Zinn (1993)
noted specifically that whereas the BHB
group has the normal slightly prograde rotation characteristic of
the overall halo, the RHB clusters by themselves seemed to possess
a zero or slightly retrograde motion, perhaps indicative of their
origin in an accretion or merger (see also
Da Costa & Armandroff
1995
for lists of these clusters and another kinematic analysis). In a rediscussion
of this issue with the most recent data
(H99),
I note that there are
two serious problems with this interpretation: first and most
important is that the RHB clusters are all drawn by definition
from the outer halo (Rgc
A second factor results from the unfortunate, and
unavoidable, fact that both samples of objects are statistically small when
we restrict ourselves to the outer halo. The nominal ``retrograde''
motion of the RHB group turns out to be entirely driven by just one cluster,
NGC 3201. Because of its location on the sky (cos
Even though we cannot increase the numbers of clusters in our
kinematical samples, we can eventually improve our knowledge of
their individual orbits which may help us isolate potential
kinematic differences. New data for absolute
proper motions and thus true three-dimensional space velocities
are steadily accumulating in both quantity and quality (see
particularly the recent work of
Dinescu et al. 1998
which also summarizes previous space motion studies). This material
can be used, albeit for smaller numbers of
clusters, to categorize the orbital types of each subsample discussed
above. Inspection of their results shows that, when the RHB clusters
are compared with the BHB clusters in the same spatial region
(8-40 kpc), there is no distinguishable difference in mean
orbital energy E or eccentricity e. Similar proportions of
clusters are found in each group with individual prograde, retrograde,
or plunging orbits. The traditional assumption of roughly isotropic
orbits (with < e >
Finally, differential age comparisons can now be performed for
several clusters in each group, since recent precise photometry
reaching well past the main-sequence turnoff has been obtained for a
number of critical RHB/BHB ``pairs'' of similar metallicity,
including the classic M3/M13 pair
(Catelan & de Freitas
Pacheco 1995;
Johnson & Bolte 1998;
Grundahl & Andersen
1998)
and NGC 288/362/1851 (see
Stetson et al. 1996;
Sarajedini et al. 1997
for a representative range of views). Although individual analyses disagree
in some details, the extremely precise comparisons in the
papers listed above make it appear unlikely that the clusters in these
comparison pairs differ strongly in age; for the M3/M13 pair in particular,
such differences are well within the ~ 1 Gyr precision of the CMD
matching methods. A view is emerging that the solution to the
long-standing ``second parameter problem'' for horizontal-branch
morphology lies in more than just age differences anmong these
clusters, perhaps in a combination of factors involving detailed
abundance differences, mixing, or even helium abundance
(Johnson & Bolte 1998;
Grundahl et al. 1998).
In the outer Palomar-type clusters as
well, the main sequence loci established from recent deep HST photometry
(Stetson et al. 1999)
translate into only very modest age
differences (
In summary, the most recent assemblage of data does not favor the view
that there are major kinematic or age differences between the Zinn
RHB and BHB clusters. We will have to continue exploring other avenues to
understand the physical differences between them.
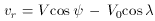
 is the angle between V and
the vector r from the Sun
to the cluster; and
is the angle between V and
the vector r from the Sun
to the cluster; and  is the
angle between V0 and r
(Frenk & White 1980;
Zinn 1985).
To use this equation, we select a group of clusters (for example, those
within a narrow range in metallicity or Galactocentric distance)
and ask what the net rotation speed V is for the group.
We assume V0 = 220 km s-1, while r,
vr,
is the
angle between V0 and r
(Frenk & White 1980;
Zinn 1985).
To use this equation, we select a group of clusters (for example, those
within a narrow range in metallicity or Galactocentric distance)
and ask what the net rotation speed V is for the group.
We assume V0 = 220 km s-1, while r,
vr,
 are
directly measured for each cluster, and
are
directly measured for each cluster, and
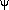 is deduced knowing r.
For an ensemble of n clusters we then plot
vLSR = (vr + V0
cos
is deduced knowing r.
For an ensemble of n clusters we then plot
vLSR = (vr + V0
cos  ) against cos
) against cos
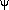 and derive the
mean slope < V > and line-of-sight dispersion
and derive the
mean slope < V > and line-of-sight dispersion
 los about the mean.
los about the mean.
 los about the mean
V are in km s-1.
los about the mean
V are in km s-1.
Group Subgroup V(rot)
 los
los
MRP 0 - 4 kpc 86 ± 40 99 ± 15
4 - 9 kpc 147 ± 27 66 ± 12
MPP 0 - 4 kpc 56 ± 37 122 ± 16
4 - 8 kpc 12 ± 31 79 ± 12
8 - 12 kpc 26 ± 63 148 ± 29
[Fe/H] <-1.7 80 ± 43 130 ± 16
Rgc>8, BHB 55 ± 59 118
± 18
Rgc>8, RHB -39 ± 83 158 ± 24
RHB ex.N3201 32 ± 89 149 ± 24
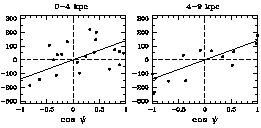
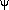 ) for the MRC clusters within
(0 < Rgc < 4) kpc
(left panel) and (4 < Rgc < 9) kpc (right panel).
) for the MRC clusters within
(0 < Rgc < 4) kpc
(left panel) and (4 < Rgc < 9) kpc (right panel).
 los ~ 120 km
s-1), and a nearly isotropic
orbit distribution (
los ~ 120 km
s-1), and a nearly isotropic
orbit distribution ( R ~
R ~

 ~
~

 ). Although these
blanket statements remain true
to first order, we now suspect that the MPC contains identifiable
subgroups and perhaps traces of separate protogalactic `fragments'
and accreted satellites. The search for these continues, in the form
of moving groups of field-halo stars, or elongated distributions of
tidal debris from individual clusters or dwarf galaxies.
). Although these
blanket statements remain true
to first order, we now suspect that the MPC contains identifiable
subgroups and perhaps traces of separate protogalactic `fragments'
and accreted satellites. The search for these continues, in the form
of moving groups of field-halo stars, or elongated distributions of
tidal debris from individual clusters or dwarf galaxies.
 10 kpc), since the outer-halo
objects necessarily have only a small range in
(cos
10 kpc), since the outer-halo
objects necessarily have only a small range in
(cos  ) and therefore
exert no leverage on V.
Is this a fossil remnant of a formation process resembling the
classic ELS model
(Eggen, Lynden-Bell,
& Sandage 1962),
whereby the inner protogalaxy went through a monolithic collapse
and spin-up?
) and therefore
exert no leverage on V.
Is this a fossil remnant of a formation process resembling the
classic ELS model
(Eggen, Lynden-Bell,
& Sandage 1962),
whereby the inner protogalaxy went through a monolithic collapse
and spin-up?
 8 kpc), whereas the BHB sample
being compared with it was drawn from all Galactocentric
distances, including large numbers from the inner halo. And, as we
have seen above, the inner metal-poor halo has a distinct prograde
rotation. We should, more correctly, compare the RHB and BHB
subgroups from within the same radial range. When this is
done (Table 1), no significant difference appears
between them.
8 kpc), whereas the BHB sample
being compared with it was drawn from all Galactocentric
distances, including large numbers from the inner halo. And, as we
have seen above, the inner metal-poor halo has a distinct prograde
rotation. We should, more correctly, compare the RHB and BHB
subgroups from within the same radial range. When this is
done (Table 1), no significant difference appears
between them.
 -1)
and large radial velocity (vr = 494 km s-1),
this single cluster has a uniquely powerful influence
on the rotation solution: if we arbitrarily remove it from the sample,
we find that V(rot) for the RHB group changes by +70 km
s-1 and makes
the result formally indistinguishable from the outer BHB group.
In summary, the radial velocity data by themselves give no
convincing evidence for net retrograde motion in any identifiable
subgroup. Finding evidence for retrograde subgroups of stars in the
halo must, instead, rely on the much larger samples of objects that
can be accumulated from field stars (see Majewski's lectures in this
volume).
-1)
and large radial velocity (vr = 494 km s-1),
this single cluster has a uniquely powerful influence
on the rotation solution: if we arbitrarily remove it from the sample,
we find that V(rot) for the RHB group changes by +70 km
s-1 and makes
the result formally indistinguishable from the outer BHB group.
In summary, the radial velocity data by themselves give no
convincing evidence for net retrograde motion in any identifiable
subgroup. Finding evidence for retrograde subgroups of stars in the
halo must, instead, rely on the much larger samples of objects that
can be accumulated from field stars (see Majewski's lectures in this
volume).
 0.66 in both RHB and BHB groups)
is also confirmed.
0.66 in both RHB and BHB groups)
is also confirmed.


 1.5 Gyr)
compared with M3 or M5, despite their much redder HB morphologies.
1.5 Gyr)
compared with M3 or M5, despite their much redder HB morphologies.