The observations of the diffuse ultraviolet background at high galactic latitudes are collected in Figure 1. The figure caption contains references to the sources of the various observations. We will, for now, assume that this radiation is extragalactic.
|
Figure 1. The plotted observations of
(assumed) extragalactic diffuse cosmic ultraviolet
background radiation (letters in Figure) have been reviewed by
Henry (1991).
The intensity in units is plotted against the wavelength of observation
in Å. Superposed on
the observations are predicted spectra of the recombination radiation
from ionized
intergalactic clouds (solid line, clouds that are expanding as the
universe expands; dashed
line, gravitationally bound clouds). Neutrino decay radiation would
also produce a spectrum
shaped like the dashed line. The observation V, shortward of Lyman
(1216 Å), is the Voyager upper limit of Holberg
(1986;
solid line: calibration of
Holberg et al. 1982,
dashed line: calibrations of
Brune et al. 1979 and
Cook et al. 1989).
The observations
longward of L |
First, we note that the extragalactic background shortward of
L
(1216 Å) is less
than 100 photons cm-2 s-1 sr-1
Å-1 (units that will be called "units" hereafter) if the
calibration of
Holberg et al. (1982)
is used (solid line in figure), or still less (dashed line)
if the calibration of
Brune et al. (1979) or
Cook et al. (1989)
is used. In contrast, all of
the observations in Figure 1 longward of 1216
Å are positive detections of 
200 units, not upper limits.
We stress that the scatter that appears in the observations of Figure 1 demonstrably reflects a spatial variation in overall intensity of the ultraviolet background on the sky, rather than either uncertainties in the observations or gross (or detailed) spectral variations. This is demonstrated most clearly by examining individual spectra, for example Figure 10 of Anderson et al. (1979). Such examination makes clear that the ultraviolet background longward of 1216 Å (at a given location) shows no trace of a decline toward shorter wavelengths. The decline is abrupt, and occurs near 1216 Å.
What is the interpretation of the remarkable spectrum of Figure 1? The striking feature of course is the ledge: no detectable radiation short of about 1216 Å; strong, well-observed radiation longward of that wavelength. Now, a ledge of just this character has been searched for ever since de Rújula and Glashow (1980) suggested that the dark matter might be massive neutrinos that might decay with the emission of an ultraviolet photon. A ledge of exactly this character was predicted, and has been vigorously searched for. For example Stecker (1980) identified a ledge in the fragmentary observations of the time, and suggested the possibility that neutrino decay radiation had actually been observed. While that particular ledge is no more, interest in the general subject remains keen (Kimble et al. 1981; Henry and Feldman 1981; Murthy and Henry 1987).
However, while we have now located an excellent ledge, the shape of the spectrum toward longer wavelengths does not fit an origin in neutrino decay radiation. The expected spectrum is given in Equation 1, as a function of redshift z (for the same equation in terms of wavelength, see Kimble et al. 1981).
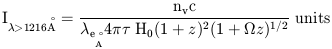
| (1) |
where nv is the local density of neutrinos of the type that
decay with the emission
of a photon, 
eÅ is the wavelength of the
emitted radiation,
is the lifetime of the
neutrinos against radiative decay, c = 3 x 1010 cm
s-1, the Hubble parameter H0 =
50 h50 km s-1 Mpc-1, 1 + z =
/ 1216 Å is the
redshift due to the expansion of the
universe, and 
= 1 (from
inflation, but see also
Dekel et al. 1993).
The spectrum of Equation 1 is shown in Figure 1
as a dashed line. The decline
to longer wavelengths is ~
-5/2 and clearly
such a decline is not supported at all by
the observations. The only hope of preserving this origin would be to
hypothesize that
some other (galactic?) source was filling in at longer wavelengths, but
if this were the
case, the observations (see the figure) would provide no evidence at all
for the neutrino
decay radiation itself. There is therefore no support whatever for the
idea that neutrino decay radiation has been detected.
Had we been able to conclude that the observed radiation actually was neutrino
decay radiation, we would have had to attribute the fact that the ledge
occurred at
a wavelength very close to that of Lyman
to chance. Let us next look at
another
potential origin where again we would ascribe the wavelength of the
ledge to coincidence:
an origin in the redshifted light of galaxies. In particular, could the
ledge be the Lyman
limit to the light from a tremendous burst of star formation in
starburst galaxies?
To have the ledge occur near 1216 Å requires that the starbursts occurred at a redshift of 0.33, and the sharpness of the ledge requires that the activity have begun and ended rather abruptly. None of this is very palatable. Even more important, Martin, Hurwitz, and Bowyer (1991) have looked very carefully and critically at the idea that the diffuse background spectrum observed longward of 1216 Å could originate in starburst activity, and do not succeed in reconciling the observations with a dominant contribution from unclustered starburst galaxies at low redshift.
Finally, we consider the idea that we are seeing redshifted extragalactic hydrogen recombination radiation and that the fact that the ledge occurs near 1216 Å is not a coincidence. The expected spectral shape for the case of gravitationally-bound clouds of ionized hydrogen is identical to that of neutrino decay radiation, and so that case may be rejected immediately on observational grounds.
The spectrum for intergalactic clouds that are expanding as the universe expands is given in Equation 2.
| (2) |
where = 2.8 x 10-13
cm3 s-1 is the effective recombination coefficient
(recombination
to n = 1 generates no L
radiation), x = 0.746 is the fraction of baryons that are
hydrogen nuclei, the local density of ionized hydrogen nuclei
n0 = 2.83 x 10-6 h250
g,
eÅ
= 1216, C = the clumping factor (which is independent of z in
this model). We take the gas temperature (which affects
) to be 8000 K, for reasons
that are given
below; our results are very insensitive to the temperature.
The spectrum of Equation 2 appears in Figure 1
as the solid line, which fits the
data acceptably well, considering that the data are obtained at many
different locations
at high galactic latitudes. The parameter
g is the
contribution to that is due to
ionized intergalactic gas. If we attribute the jump at z = 0 of
300 units that is shown
by the observations (Figure 1) to intergalactic
recombination radiation, we find that
| (3) |
describes the observations.
At this point, we recapitulate facts that bear directly on the
possibility of detecting
redshifted Lyman recombination
radiation from ionized intergalactic gas.
The very small spatial fluctuations observed by COBE indicate that the dark matter was an essential ingredient in the formation of structure among the baryons following recombination. The structured dark matter was already there, and following recombination the neutral hydrogen and helium fell into the potential wells, creating the structure we observe today.
Intergalactic space was left free of neutral hydrogen. Indeed, intergalactic space is astonishingly free of neutral hydrogen, the density being < 4.5 x 10-14 h50 cm-3 (Steidel and Sargent 1987). This means that in a volume of 50 cubic megaparsecs, where there is on average one galaxy, of mass 8 x 1010 solar masses (Allen 1973), there are < 50,000 solar masses of (smoothly distributed) neutral intergalactic gas. Galaxy formation gathered up all of the baryons except a fraction < 6 x 10-7, an efficient process indeed - unless intergalactic hydrogen is highly ionized. Observations of the cosmic microwave background (Mather et al. 1990) show that such intergalactic hydrogen cannot be at very high temperatures (Rogers and Field 1991). At lower temperatures, recombination becomes more efficient, especially if the intergalactic gas is clumped. The clumping C = < n2e > / < ne >2 = 1.5 x 107 for galaxies, and is unknown for ionized intergalactic gas.
The final fact that bears directly on the search for recombination
radiation is that
only a small part of the expected baryonic matter is accounted for by
matter that has
already been detected. For example
Persic and Salucci
(1992)
estimate the baryon mass
density of the universe due to the stars in galaxies and hot gas in
clusters and groups of galaxies. They find
b = 0.003, which is
less than 10 percent of the lower limit
predicted by standard primordial nucleosynthesis which implies that the
great majority of the baryons in the universe are as yet unseen.
We are now prepared to explore the consequences of equation 3. Persic
and Salucci quote
Kolb and Turner (1990)
and Peebles et
al. (1991)
in giving
b
h250 = 0.06 as the
most probable value for the baryon density from nucleosynthesis. We take
g =
b,
that is, essentially all of the baryons are intergalactic ionized
hydrogen. Insertion into
equation 3 then gives C / h50 = 50,000. Notice that this
clumping is vastly less than
for the visible matter (galaxies) in the universe. The clumps of ionized
baryons in the
universe are much larger in relation to their separation than are galaxies.
We have seen that the intergalactic medium is unquestionably highly ionized. What causes this ionization? There is some controversy over this. Meiksin and Madau (1993) provide several models in which the observed QSOs can provide the required ionizing photons at early epochs, and we accept their conclusion.
However, our highly clumped ionized intergalactic medium has much more severe problems. For h50 = 1, the recombination time of our clouds is only 1.3 x 107 years, and for h50 = 2 the recombination time is 6.3 x 106 years. Thus, if this interpretation of the diffuse high galactic latitude diffuse background is correct, a strong additional source of ionizing photons is required. Just such a source, radiative decay of neutrinos, has been proposed by Sciama (1993, e.g., in which Sciama references defenses of his neutrinos against the conclusions of Davidsen et al. 1991, who failed to observe a neutrino decay line from the cluster of galaxies A665). Sciama's neutrinos decay with the emission of photons that are just capable of ionizing hydrogen (hence our assumed temperature, above, of ~ 8000 K). Sciama's neutrinos, in our present picture, would be the dark matter into which the baryons all fell following recombination. In every potential well, most (or rather, in most cases, all) of the hydrogen was re-ionized by Sciama's neutrinos. In exceptional cases dissipation occurred and quasars and galaxies formed. In most cases, in contrast, the hydrogen simply re-ionized and expanded out of the well, forming our present clouds that are expanding with the universe. Such clouds would be extremely hard to detect, either in emission or absorption, because of the very large velocity dispersion that is expected.
In the present picture there is no way of avoiding Sciama's neutrinos (or their
equivalent). If we assume that all of closure density
( = 1) is ionized gas (that is,
we ignore the nucleosynthesis argument), we obtain present-day
recombination times
that are of the order of the Hubble time, but the recombination time
earlier (when the clouds were denser) would still be too short.
We conclude that if the high-galactic latitude diffuse ultraviolet background is extragalactic in origin, then its observed spectrum implies all of: a) detection of the baryonic dark matter; b) detection of the effects of the non-baryonic dark matter (Sciama neutrinos); and c) evidence for new physics beyond the standard model of elementary particle physics (Sciama neutrinos). As that would be an important set of discoveries indeed, we now turn to the observations at lower galactic latitudes in an effort to account for the high galactic latitude signal as being galactic, rather than extragalactic, in character.