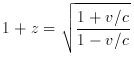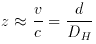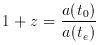The redshift z of an object is the fractional doppler shift of its emitted light resulting from radial motion
where
where c is the speed of light. Many feel that it is wrong to view
relativistic redshifts as velocities (eg,
Harrison 1993), but I
simply do not agree. The difference between an object's measured
redshift and its cosmological redshift is due to its (radial)
peculiar velocity; ie, we define the cosmological redshift as
that part of the redshift due solely to the expansion of the Universe,
or Hubble flow. For small v / c, or small distance
d, in the
expanding Universe, the velocity is linearly proportional to the
distance (and all the distance measures, eg, angular diameter
distance, luminosity distance, etc, converge)
where DH is the Hubble distance (see above). But this
is only true for small redshifts!
(It is very important to note that galaxy redshift surveys, when
presenting redshifts as radial velocities, always use the
non-relativistic approximation v = c z, even when it is not
appropriate physically; eg.,
Fairall 1992.)
In terms of cosmography, the cosmological redshift is directly related
to the scale factor a (t), or the ``size'' of the Universe. For an
object at redshift z
where a (t0) is the size of the Universe at the
time the light from
the object is observed, and a (te) is the size
at the time it was emitted.
Redshift is almost always determined with respect to us (or the frame
centered on us but stationary with respect to the microwave
background), but it is possible to define the redshift z12
between objects 1 and 2, both of which are cosmologically redshifted
relative to us: the redshift z12 of an object at
redshift z2
relative to a hypothetical observer at redshift z1 <
z2 is given by
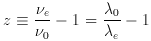
 0 and
0 and  0 are the observed
frequency and
wavelength, and
0 are the observed
frequency and
wavelength, and  e and
e and  e are the emitted.
Redshift is related to radial velocity v by
e are the emitted.
Redshift is related to radial velocity v by