


The comoving distance between two events at the same redshift or
distance but separated on the sky by some angle 
 is
DM
is
DM 
 and the transverse comoving
distance DM
(so-denoted for a reason explained below) is simply related to the
line-of-sight comoving distance DC:
and the transverse comoving
distance DM
(so-denoted for a reason explained below) is simply related to the
line-of-sight comoving distance DC:
where the trigonometric functions sinh and sin account for what
is called ``the curvature of space.'' (Space curvature depends on the
particular coordinate system chosen, so it is not intrinsic; a change
of coordinates makes space flat; the only intrinsic curvature is
space-time curvature, which is related to the local mass-energy
density or really stress-energy tensor.) For
(Weinberg 1972,
p. 485;
Peebles 1993,
pp. 320-321). Some (eg.,
Weedman 1986,
pp. 59-60) call this distance measure ``proper
distance,'' which, though common usage, is bad style.
(1)
(Although these notes follow the Peebles derivation, there is a
qualitatively distinct method using what is known as the
development angle
The comoving distance happens to be equivalent to the proper
motion distance (hence the name DM), defined as
the ratio of the
actual transverse velocity (in distance over time) of an object to its
proper motion (in radians per unit time)
(Weinberg 1972,
pp. 423-424). The proper motion distance is plotted in
Figure 1. Proper motion distance is used, for example,
in computing radio jet velocities from knot motion.
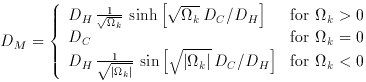

 = 0,
there is an analytic solution to the equations
= 0,
there is an analytic solution to the equations
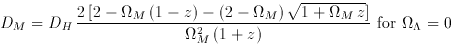
 , which
increases as the Universe evolves.
This method is preferred by relativists such as Misner, Thorne &
Wheeler 1973, pp. 782-785).
, which
increases as the Universe evolves.
This method is preferred by relativists such as Misner, Thorne &
Wheeler 1973, pp. 782-785).
1 The
word ``proper'' has a specific use in relativity. The proper
time between two nearby events is the time delay between the events
in the frame in which they take place at the same location, and the
proper distance between two nearby events is the distance
between them in the frame in which they happen at the same time. It
is the distance measured by a ruler at the time of observation. The
transverse comoving distance DM is not a proper
distance - it is a proper distance divided by a ratio of scale
factors. Back.