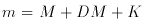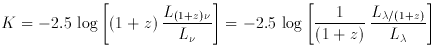The luminosity distance DL is defined by the relationship between bolometric (ie, integrated over all frequencies) flux S and bolometric luminosity L:
It turns out that this is related to the transverse comoving distance
and angular diameter distance by
(Weinberg 1972,
pp. 420-424;
Weedman 1986,
pp. 60-62). The latter
relation follows from the fact that the surface brightness of a
receding object is reduced by a factor (1 + z)-4, and
the angular
area goes down as DA-2. The luminosity
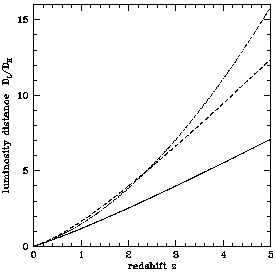
distance is plotted in Figure 3.
Figure 3. The dimensionless luminosity
distance DL / DH. The three curves are for
the three world models, (
If the concern is not with bolometric quantities but rather with
differential flux S
where z is the redshift, the ratio of luminosities equalizes the
difference in flux between the observed and emitted bands, and the
factor of (1 + z) accounts for the redshifting of the bandwidth.
Similarly, for differential flux per unit wavelength,
(Peebles 1993,
pp. 330-331;
Weedman 1986,
pp. 60-62). In this
author's opinion, the most natural flux unit is differential flux per
unit log frequency or log wavelength
where
The distance modulus DM is defined by
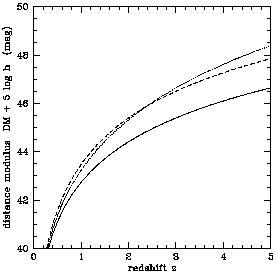
Figure 4. The distance modulus DM.
The three curves are for
the three world models, (
because it is the magnitude difference between an object's observed
bolometric flux and what it would be if it were at 10 pc
(don't ask me, ask an astronomer!). The distance modulus is plotted
in Figure 4. The absolute magnitude M is the
astronomer's measure of luminosity, defined to be the apparent
magnitude the object in question would have if it were at 10 pc, so
where K is the k-correction
(eg., Oke & Sandage 1968).
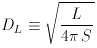
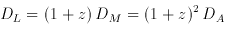
M, 
) =
(1, 0), solid; (0.05, 0), dotted; and (0.2, 0.8), dashed.
and luminosity L,
as is usually
the case in astronomy, then a correction, the k-correction,
must be applied to the flux or luminosity because the redshifted
object is emitting flux in a different band than that in which you are
observing. The k-correction depends on the spectrum of the object in
question, and is unnecessary only if the object has spectrum
L = constant. For any other spectrum
the differential flux S
is related to the differential luminosity
L by
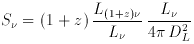
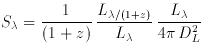
S = 
S for which there is no redshifting of the bandpass so
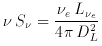
e= (1 +
z) is the emitted frequency.
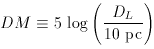
M, ) =
(1, 0), solid; (0.05, 0) dotted; and (0.2, 0.8) dashed.
