10.3.2 Possible Systematic Effects

Here we discuss the physical effects that could systematically bias the method rather than systematic effects in the data which are covered in Sec. 10.5. A thorough discussion of possible systematic effects is presented in the Appendix to BFD where they investigate the dependence of the D_n- relation on absolute magnitude, mass-to-light ratio and cluster properties. They found no significant effects; their plot of residual radial velocity vs. galaxy absolute magnitude is reproduced in Figure 23. Mass-to-light ratio and cluster effects are discussed below.

Figure 23. The logarithm of the ratio of predicted distance corrected for Malmquist bias, to radial velocity in the cosmic microwave background frame, log10(V/R), as a function of absolute B magnitude of 182 galaxies in clusters, taken from BFD. Galaxies from both the 7S sample (open squares) and BFD (stars) are included.

The constraints on M/L implied by the existence of the fundamental plane led Silk (1989) to suggest that the environments of ellipticals might act to modify M/L and thus cause the zero-point of the D_n- relation to vary within a cluster or between clusters. Silk proposed that such an effect might introduce spurious large scale motions. This possibility has been tested by Lucey et al. (1991b) who found no significant systematic dependence on the zero-point of the relation over a factor of 150 in projected local galaxy density in the Coma cluster. Similarly BFD found no dependence of the peculiar velocity of cluster ellipticals on M/L (as characterized by the strength of the Mg₂ index of the stellar population at a given ). There are hints in BFD that in a minority of field and group ellipticals the global parameters, in particular line strengths, might be altered by the presence of an intermediate age population. Schweizer et al. (1990), noted that the presence of fine morphological structures (jets, shells, isophote distortions) also loosely correlate with indicators of the age of the stellar population such that galaxies exhibiting fine structure appear to have a younger component which they suggest was formed at the same time as the event that generated the structure. Gregg (1992) has taken this further and demonstrated that those few galaxies with the most marked morphological peculiarities have systematically positive peculiar motions. While the number of affected galaxies appears to be very small, the effect of these correlations on the application of the D_n- method needs to be evaluated further.

Djorgovski et al. (1988) investigated the possibility that cluster properties such as richness, velocity dispersion, and density might affect the form of the D_n- relation. They tentatively suggested that cluster richness caused a variation in the slope and intercept of the relation within clusters, possibly due to the effects of interactions. However, these effects were not confirmed by BFD (see Figure 24) and are not present in the detailed study of the Coma cluster by Lucey et al. (1991b).

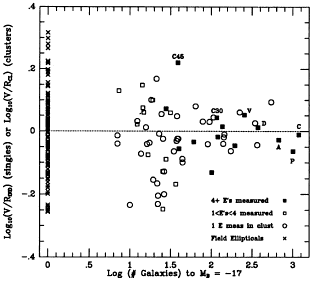
Figure 24. Ordinate as Figure 23 shown as a function of the number of galaxies in a cluster with MB < -17 (from BFD). The number of ellipticals in each cluster is indicated. Field galaxies are included at richness 1. The following clusters are identified: Virgo (V), Perseus (P), Coma (C), Abell 1367 (A), Cen 45 (C45), and Cen 30 (C30).

The overall agreement of other distance indicators with D_n- (see Sec. 11) tends to confirm that environmental effects are not generating mythical large scale flows. Indeed, a remarkable set of coincidences would be needed to explain the large scale pattern of peculiar motions in terms of small M/L changes. This is not to say, however, that there are no clusters where the distance determined by D_n- is discrepant with that of another method. The most serious case is Abell 2634, where Aaronson et al. (1986) find the cluster to be at rest with respect to the Hubble flow, and Lucey et al. (1991a), using a D_V- relation (based on V band photometry rather than B band observations), find a peculiar velocity of > +3000 km s^-1. Such discrepancies need to be resolved.

On balance it seems that environmental effects have not been shown to bias D_n- as a standard candle but the absence of a detailed physical model to describe the method demands continuing care to ensure that such systematic effects do not enter into the future application of the method.