Consider a source of diffuse background radiation having a continuum volume
emissivity, 
(
, t) as a function of
wavelength, , and cosmic time
t 
t0. The
background
intensity due to this source at a given received wavelength,
0, results as the
integration
of the redshifted contributions from all epochs. The background
generated during
a time interval dt is accumulated over the pathlength cdt
where c is the speed of light.
If a(t) / a0 denotes the ratio of expansion of the
Universe between the epoch of emission
and today, the received intensity due to emission within dt is therefore
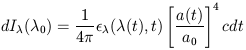
| (A1) |
where the emissivity is evaluated at the appropriate blue-shifted
wavelength of emission,
(t) =
0a(t) /
a0. The factor in square brackets takes into account the
dilution of the intensity due to the expansion of the Universe (as per
Liouville's Theorem expressed in
the adopted intensity units of photons s-1 cm-2
sr-1 Å-1). Integrating eq. (1) over
the age of the Universe gives then for the total background intensity
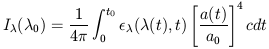
| (A2) |
It is convenient to change variables from cosmic time to redshift, (1 + z) = a0 / a(t), using the standard expression for a Friedman Universe
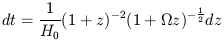
| (A3) |
where H0 is the Hubble Constant. This leads to
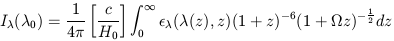
| (A4) |
where (z) =
0 / (1 + z).
Equation (A4) is the general expression for the accumulated background from any continuum emission source. The special case of redshift smeared monochromatic line emission is also of interest. In this case we have for the emissivity
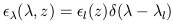
| (A5) |
Where l is the
rest wavelength of the transition in question. Inserting (A5) into (A4)
leads to the following expression for the intensity of the resulting
continuum background
at wavelengths 0
l
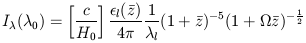
| (A6) |
where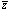 
=
0 /
l - 1 is the
redshift of emission.