


3.1 Stellar Dynamical Mass Measurement
Dynamical mass measurement is conceptually simple. If random motions are
small, as they are in a gas, then the mass M(r) within radius
r is M(r) =
V2 r / G. Here V is the rotation
velocity and G is the gravitational
constant. In stellar systems, some dynamical support comes from random
motions, so M(r) depends also on the velocity dispersion
 . The
measurement technique is best described in the idealized case of spherical
symmetry and a velocity ellipsoid that points at the center. Then
the first velocity moment of the collisionless Boltzmann equation gives
. The
measurement technique is best described in the idealized case of spherical
symmetry and a velocity ellipsoid that points at the center. Then
the first velocity moment of the collisionless Boltzmann equation gives
Here
There is one tricky problem with this analysis, and it follows directly
from Equation 2. Rotation and random motions contribute similarly to
M(r),
but the
Much effort has gone into finding the answer. The most powerful technique is
to construct self-consistent dynamical models in which the density distribution
is the linear combination
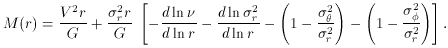
 r,
r,

 , and
, and

 are the radial and
azimuthal components of the velocity dispersion. The density
are the radial and
azimuthal components of the velocity dispersion. The density
 is not the total mass density
is not the total mass density
 ; it is the density
of the luminous tracer population whose kinematics we measure. We never see
; it is the density
of the luminous tracer population whose kinematics we measure. We never see
 , because the stars that
contribute most of the light contribute almost none of the mass. Therefore we
assume that
, because the stars that
contribute most of the light contribute almost none of the mass. Therefore we
assume that  (r)
(r)
 volume brightness. All
quantities in Equation 2
are unprojected. We observe brightnesses and velocities after projection and
blurring by a point-spread function (PSF). Information is lost in both
processes. Several techniques have been developed to derive unprojected
quantities that agree with the observations after projection and PSF
convolution. From these, we derive the mass distribution M(r) and
compare it
to the light distribution L(r). If M/L(r) rises rapidly as
r -> 0, then we have found a central dark object.
volume brightness. All
quantities in Equation 2
are unprojected. We observe brightnesses and velocities after projection and
blurring by a point-spread function (PSF). Information is lost in both
processes. Several techniques have been developed to derive unprojected
quantities that agree with the observations after projection and PSF
convolution. From these, we derive the mass distribution M(r) and
compare it
to the light distribution L(r). If M/L(r) rises rapidly as
r -> 0, then we have found a central dark object.
 2 r /
G term is multiplied by a factor that depends on the
velocity anisotropy and that can be less than 1. Galaxy formation can easily
produce a radial velocity dispersion
2 r /
G term is multiplied by a factor that depends on the
velocity anisotropy and that can be less than 1. Galaxy formation can easily
produce a radial velocity dispersion
 r that is larger than the
azimuthal components
r that is larger than the
azimuthal components

 and
and 
 . Then the third and
fourth terms inside the brackets in Equation 2 are negative; they can be as
small as -1 each. In fact, they can largely cancel the first two terms,
because the second term cannot be larger than +1, and the first is
. Then the third and
fourth terms inside the brackets in Equation 2 are negative; they can be as
small as -1 each. In fact, they can largely cancel the first two terms,
because the second term cannot be larger than +1, and the first is
 1
in many galaxies. This explains why ad hoc anisotropic models have
been so successful in explaining the kinematics of giant ellipticals without
BHs. But how anisotropic are the galaxies?
1
in many galaxies. This explains why ad hoc anisotropic models have
been so successful in explaining the kinematics of giant ellipticals without
BHs. But how anisotropic are the galaxies?
 =
=
 Ni
Ni
 i of the
density distributions
i of the
density distributions
 i of the
individual orbits that are allowed by the
gravitational potential. First the potential is estimated from the light
distribution. Orbits of various energies and angular momenta are then
calculated
to construct a library of time-averaged density distributions
i of the
individual orbits that are allowed by the
gravitational potential. First the potential is estimated from the light
distribution. Orbits of various energies and angular momenta are then
calculated
to construct a library of time-averaged density distributions
 i.
Finally, orbit occupation numbers Ni are derived so
that the projected and
PSF-convolved model agrees with the observed kinematics. Some authors also
maximize
i.
Finally, orbit occupation numbers Ni are derived so
that the projected and
PSF-convolved model agrees with the observed kinematics. Some authors also
maximize  Ni
lnNi, which is analogous to an entropy. These
procedures allow the stellar distribution function to be as anisotropic as it
likes in order (e.g.) to try to explain the observations without a BH. In
the end, such models show that real galaxies are not extremely
anisotropic. That
is, they do not take advantage of all the degrees of freedom that the physics
would allow. However, this is not something that one could take for granted.
Because the degree of anisotropy depends on galaxy luminosity, almost all BH
detections in bulges and low-luminosity ellipticals (which are nearly
isotropic)
are based on stellar dynamics, and almost all BH detections in giant
ellipticals (which are more anisotropic) are based on gas dynamics.
Ni
lnNi, which is analogous to an entropy. These
procedures allow the stellar distribution function to be as anisotropic as it
likes in order (e.g.) to try to explain the observations without a BH. In
the end, such models show that real galaxies are not extremely
anisotropic. That
is, they do not take advantage of all the degrees of freedom that the physics
would allow. However, this is not something that one could take for granted.
Because the degree of anisotropy depends on galaxy luminosity, almost all BH
detections in bulges and low-luminosity ellipticals (which are nearly
isotropic)
are based on stellar dynamics, and almost all BH detections in giant
ellipticals (which are more anisotropic) are based on gas dynamics.