3.3. Forcing by Satellites

One of the first possible explanations for the warp of the Galaxy was the tidal perturbation by the Magellanic Clouds. Hunter & Toomre (1969) however showed that these are too weak to have a strong effect. Lately this idea has been revived, however, by the work of Weinberg (1995, 1998). He presented a model for which he calculated the self-consistent response (wake) of the Galactic dark halo to the orbiting Clouds. This wake turns out to be rather massive, and to be strongest at a radius inside that of the Cloud orbit; both help to boost the tidal effect of the wake to dominate that of the Cloud itself. With such halo-enhanced tides, he was able to reproduce the observed Galactic warp amplitude.

Weinberg's model requires some tuning in order to achieve the amplitudes observed. It also makes several assumptions:

1. The Cloud orbit is modelled as a quasi-periodic orbit, i.e., the dynamical friction-induced decay of the orbit is ignored. This means that the model disk is perturbed at a constant set of frequencies, and it has time to build up its response to these perturbations. In reality, however, the frequencies at which the disk is perturbed are continuously increasing.
2. The halo's back-reaction to the disk precession is not included in the calculations. In fact, in these models the halo is assumed to be spherically symmetric (before the LMC perturbs it). We have seen above, however, that the halo couples very effectively to a precessing misaligned disk.

These caveats suggest that satellites may not generally be responsible for causing warps in their hosts.

Some extra evidence against the LMC as cause comes from studying the orientation of the warp and of the LMC orbit. Garcia-Ruiz et al (in prep.) made a very simple disk/halo/satellite system. The model consists of a rigid spinning disk, a flattened dark halo, and a satellite orbiting on a circular orbit. The equations of motion for the polar coordinates (, ) of the disk axis (halo axis = 0) can then be linearized in terms of (x, y) = ( cos, sin) to

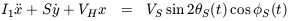
	(2)
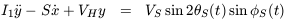
	(3)

where I₁ is the moment of inertia of the disk about its diameter, S is the spin of the disk, V_H is the torque per unit angle exterted by the halo, V_S parameterized the satellite tidal field strength and the satellite orbit follows = _S(t), = _S(t). This equation is easily solved: for the case of a polar orbit with _S = 90°, _S = _St the solution is (with = (V_H - 4I_{1 S}²)² - (2_SS)²)

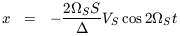
	(4)
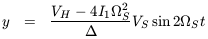
	(5)

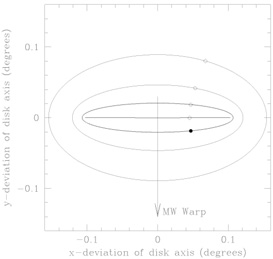
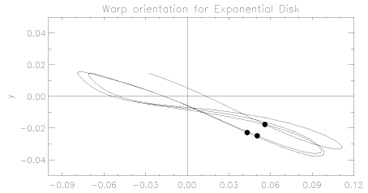
Figure 3. Top: precession path of a rigid disk in a flattened halo, perturbed by an orbiting satellite. The dots indicate the position corresponding to the current phase of the LMC in its orbit, which is in the yz plane fro halo potential flattenings of 0 (solid), 0.05, 0.1, 0.15, 0.2. The direction of the observed tilt of the axis of the outer disk of the Milky Way is indicated by the arrow. Bottom: The warp direction (direction of the average alignment of the outer disk with reference to the inner disk plane) for an exponential disk consisting of centrally-pivoted concentric spinning rings. In both cases, the response of the disk is primarily to tilt in the plane perpendicular to the satellite orbit, unlike what is observed in the Galaxy / LMC system.

The precession path of such a rigid disk, for Galaxy / LMC parameters, is shown in Fig 3. The dominant effect of the satellite perturbation is to make the disk axis nod perpendicular to the satellite orbital plane, a consequence of the slow satellite orbital frequency compared to the natural precession frequency of the disk. The orientation is independent of the satellite mass, or of the strength of the tidal field; it is governed only by the frequencies of the satellite and disk.

An extension of this calculation to a disk consisting of many rigid, precessing rings all anchored to a common center shows the same trend (Fig 3): the warp orientation (defined as the direction along which the inner and outer disk orientations differ maximally) is perpendicular to the satellite orbital plane.

By contract, the LMC orbit lies in the plane along which the Galactic warp is strongest.

A full N-body simulation of a disk / galaxy / LMC system, including halo back-reaction on the disk, shows the same effects. It appears that the wake of the satellite in the halo basically acts in phase with the satellite, and so mostly changes the amplitude of the tides but not their orientation. The backreaction of the halo on the precessing disk is more difficult to predict in these analytical models, as it can act both as a damping or as a destabilizing factor (see discussion on normal modes above); our numerical experiments in simulating the Galaxy / LMC situation have in not turned up any cases where the disk response was as strong as observed in the Milky Way, or oriented as observed.

Interestingly, the Sagittarius dwarf has an orbit almost at right angles to that of the LMC. It could therefore in principle produce a response in the disk of the right phase (but see Binney 2000). However, at this moment the mass of the Sgr dwarf is still rather uncertain, and it is not clear whether it could raise sufficiently strong tides. It is also in a sufficiently small orbit that the tides will be very asymmetric (Ibata & Razoumov 1998).

All in all, therefore, it appears that satellites as an explantion of the warp of the Galaxy, and by extension as a generic model for warps in other galaxies, pose some difficulties.