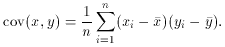4.1 Sample Moments
Let x1, x2, x3,
. . . . ., xn be a sample of size n from a
distribution
whose theoretical mean is µ and variance
 2. This is known as the
sample population. The sample mean,
2. This is known as the
sample population. The sample mean,
 is then defined as
is then defined as
which is just the arithmetic average of the sample. In the limit
n ->
Similarly, the sample variance, which we denote by
s2 is
which is the average of the squared deviations. In the limit n ->
In the case of multivariate samples, for example, (x1,
y1), (x2, y2),
. . ., the sample means and variances for each variable are calculated as
above. In an analogous manner, the sample covariance can be calculated
by
In the limit of infinite n, (28), not surprisingly, also approaches
the theoretical covariance (10).
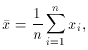
 ,
this can be shown to approach the theoretical mean,
,
this can be shown to approach the theoretical mean,
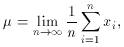
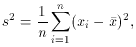
 ,
this also approaches the theoretical variance
,
this also approaches the theoretical variance
 2.
2.