


4.3 Estimator for the Poisson Distribution
Suppose we have n measurements of samples, x1, x2, x3, . . ., xn, from a Poisson distribution with mean µ. The likelihood function for this case is then
To eliminate the product sign, we take the logarithm
Differentiating and setting the result to zero, we when find
which yields the solution
Equation (39), of course, is just the sample mean. This is of no
great surprise, but it does confirm the often unconscious use of
(39).
The variance of
Applying this to the sample mean and rearranging the terms, we thus
have
Expanding the square of the sum, we find
If now the expectation value is taken, the cross term vanishes, so
that
As the reader may have noticed, (43) was derived without reference
to the Poisson distribution, so that (43) is, in fact, a general
result: the variance of the sample mean is given by the variance of
the parent distribution, whatever it may be, divided by the sample
size.
For a Poisson distribution,
where have substituted the estimated value
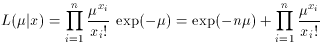
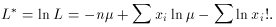
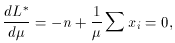
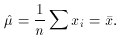
 can be found by
using (33); however, in this
particular case, we will use a different way. From (9) we have the
definition
can be found by
using (33); however, in this
particular case, we will use a different way. From (9) we have the
definition
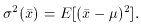
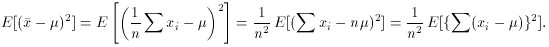
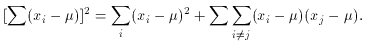
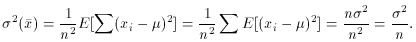
 2 = µ, so that the error on the estimated
Poisson mean is
2 = µ, so that the error on the estimated
Poisson mean is
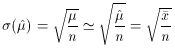
 for the theoretical
µ.
for the theoretical
µ.