


4.5 The Weighted Mean
We have thus far discussed the estimation of the mean and standard deviation from a series of measurements of the same quantity with the same instrument. It often occurs, however, that one must combine two or more measurements of the same quantity with differing errors. A simple minded procedure would be to take the average of the measurements. This, unfortunately, ignores the fact that some measurements are more precise than others and should therefore be given more importance. A more valid method would be to weight each measurement in proportion to its error. The maximum likelihood method allows us to determine the weighting function to use.
From a statistics point of view, we have a sample x1,
x1, . . , xn,
where each value is from a Gaussian distribution having the same mean
µ but a different standard deviation
 i. The
likelihood function is thus the same as (45), but with
i. The
likelihood function is thus the same as (45), but with
 replaced by
replaced by
 i. Maximizing
this we then find the weighted mean
i. Maximizing
this we then find the weighted mean
Thus the weighting factor is the inverse square of the error, i.e.,
1 /
Using (33), the error on the weighted mean can now be shown to be
Note that if all the
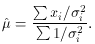
 i2. This corresponds to our
logic as the smaller the
i2. This corresponds to our
logic as the smaller the
 i, the larger
the weight and vice-versa.
i, the larger
the weight and vice-versa.
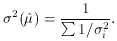
 i are the
same, the weighted mean reduces to the
normal formula in (49) and the error on the mean to (50).
i are the
same, the weighted mean reduces to the
normal formula in (49) and the error on the mean to (50).