


3.1. Spatial flatness
Of the listed properties, spatial flatness is the only one which refers to the global properties of the Universe. (1) It is particularly pertinent because of the original strong statements that spatial flatness was an inevitable prediction of inflation, later retracted with the discovery of a class of models - the open inflation models [8, 9] - which cunningly utilize quantum tunnelling to generate homogeneous open Universes. In the recent `tunnelling from nothing' instanton models of Hawking and Turok [9], any observed curvature has the interesting interpretation of being a relic from the initial formation of the Universe which managed to survive the inflationary epoch.
If we convince ourselves that, to a high degree of accuracy, the Universe is spatially flat, that will strengthen the likelihood that the simplest models of inflation are correct. However, an accurate measurement of the curvature is not a test of the full inflationary paradigm, because whatever the outcome of such a measurement there do remain inflation models which make that prediction. This point has recently been stressed by Peebles [7]. The likelihood will have shifted to favour some inflation models at the expense of others, but the total likelihood of inflation will be unchanged. (2) Only if a rival class of theories can be invented, which predict say a negative-curvature Universe in a way regarded as more compelling than the open inflation models, will measurements of the curvature acquire the power to test the inflationary paradigm.
I should also mention that the standard definition of inflation - a period where the scale factor a(t) undergoes accelerated expansion - is a rather general one, and in particular any classical solution to the flatness problem using general relativity must involve inflation. This follows directly from writing the Friedmann equation as
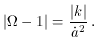
An example is the pre big bang cosmology [11], which is now viewed as a novel type of inflation model rather than a separate idea. This makes it hard to devise alternative solutions to the flatness problem; open inflation models use quantum tunnelling but in fact still require classical inflation after the tunnelling, and presently the only existing alternative is the variable-speed-of-light theories [10] which violate general relativity.
Before continuing on to the properties of perturbations in the Universe, there's a final point worth bearing in mind concerning inflation as a theory of the global Universe. As I've said, there now seems little prospect that any observations will come along which might rule out the model. But it is interesting that while that is true now, it was not true when inflation was first devised. An example is the question of the topology of the Universe. We now know that if there is any non-trivial topology to the Universe, the identification scale is at least of order the Hubble radius, and I expect that that can be consistent with inflation (though I am unaware of any detailed investigation of the issue). However, from observations available in 1981 it was perfectly possible that the identification scale could have been much much smaller. Since inflation will stretch the topological identification scale, that would have set an upper limit on the amount of inflation strong enough to prevent it from solving the horizon and flatness problems. The prediction of no small-scale topological identification has proven a successful one. Another example of a test that could have excluded inflation, but didn't, is the now-observed absence of a global rotation of our observable Universe [12].
1 Inflation is also responsible for solving the horizon problem, ensuring a Universe close to homogeneity, but this is no longer a useful test as it is already observationally verified to high accuracy through the near isotropy of the cosmic microwave background. Back
2 Indeed, the only existing alternative to inflation in explaining spatial flatness is the variable-speed-of-light (VSL) theories [10], which may be able to solve the problem without inflation, though at the cost of abandoning Lorentz invariance. There are no available alternatives at all to inflation in explaining an open Universe, so one might say that observation of negative curvature modestly improves the likelihood of inflation amongst known theories, by eliminating the VSL theories from consideration. Back