1.2. Photoionization Equilibrium
At every point in a optically thin, pure hydrogen medium of neutral density nHI, the photoionization rate per unit volume is
where J
At equilibrium, this is balanced
by the rate of radiative recombinations p + e -> H +
where ne and np are the number
densities of electrons and protons,
and
Consider, as an illustrative example, a point in an intergalactic H II region
at (say) z = 6, with density
We then have for the photoionization timescale:
and for the recombination timescale:
As in photoionization equilibrium nHI /
tion = np / trec, these
values imply nHI / np
A source radiating ultraviolet photons at a finite rate cannot ionize an
infinite region of space, and
therefore there must be an outer edge to the ionized volume (this is true
unless, of course,
there is a population of UV emitters and all individual H II regions have
already overlapped). One fundamental characteristic of the problem is the
very small value of the mean free path for an ionizing photon if the hydrogen
is neutral,
(
(assuming T is constant in space), where the brackets are the space
average of the product of the local proton and
electron number densities, and the factor C > 1 takes into
account the degree
of clumpiness of the IGM. If ionized gas with electron density
ne density filled uniformly a fraction 1/C of
the available volume, the
rest being empty space, the mean square density would be <
ne2 >
= ne2 / C = < ne
>2 C.
The IGM is completely reionized when one ionizing photon has been emitted
for each H atom by the radiation sources, and when the rate of emission of
UV photons per unit (comoving) volume balances the radiative recombination
rate, so that hydrogen atoms are photoionized faster than they can recombine.
The complete reionization of the Universe manifests itself
in the absence of an absorption trough in the spectra of galaxies and
quasars at high redshifts. If the IGM along the line-of-sight to a distant
source were neutral, the resonant scattering at the wavelength of the
Ly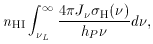
is the mean
intensity of the ionizing radiation
(in energy units per unit area, time, solid angle, and frequency interval),
and hP is the Planck constant. The photoionization
cross-section for hydrogen in the ground state by photons
with energy hP
(above the threshold
hP L = 13.6 eV)
can be usefully approximated by
per unit volume,
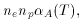
A =
< 
n
ve > is the radiative recombination
coefficient, i.e. the product of the electron capture cross-section
n and the electron
velocity ve, averaged over
a thermal distribution and summed over all atomic levels n. At
the commonly encountered gas temperature of 104 K,
A = 4.2 x
10-13 cm3 s-1.
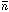H = (1.6 x 10-7
cm-3)
(1 + z)3 = 5.5 x 10-5 cm-3. The
H II region surrounds a putative
quasar with specific luminosity
L = 1030
(L /
)2 ergs s-1
Hz-1, and the point in question is at a distance
of r = 3 Mpc from the quasar. To a first approximation, the mean
intensity is
simply the radiation emitted by the quasar reduced by geometrical dilution,
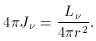
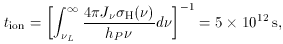
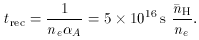
10-4, that is,
hydrogen is very nearly completely ionized.
L
nH)-1 = 0.9 kpc at threshold, much smaller than
the radius of the ionized region. If the source spectrum is steep enough
that little energy is carried out by more penetrating, soft X-ray photons,
we have one nearly completely ionized H II region, sepated from the outer
neutral IGM by a thin transition layer or `ionization-front'.
The inhomogeneity of the IGM is of primary importance for understanding the
ionization history of the Universe, as denser gas recombines faster and is
therefore ionized at later times than the tenuous gas in underdense regions.
An approximate way to study the effect of inhomogeneity is to write the
rate of recombinations as
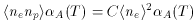
(2p -> 1s; hP
= 10.2 eV)
transition of atomic hydrogen
would remove all photons blueward of
Ly off the line-of-sight. For any
reasonable density of the IGM, the scattering optical depth is so large that
detectable absorption will be produced by relatively small column (or surface)
densities of intergalactic neutral hydrogen.