


2.2. Intergalactic Continuum Opacity
Even if the bulk of the baryons in the Universe are fairly well ionized
at all redshifts z
 5, the residual neutral
hydrogen still present
in the Ly
5, the residual neutral
hydrogen still present
in the Ly forest clouds and
Lyman-limit systems
significantly attenuates the ionizing flux from cosmological distant sources.
To quantify the degree of attenuation we have to introduce the concept of an
effective continuum optical depth
forest clouds and
Lyman-limit systems
significantly attenuates the ionizing flux from cosmological distant sources.
To quantify the degree of attenuation we have to introduce the concept of an
effective continuum optical depth
 eff along the line-of-sight
to redshift z,
eff along the line-of-sight
to redshift z,
where the average is taken over all lines-of-sight. Negleting absorption due
to helium, if we characterize the
Ly
where
If we extrapolate the NHI-1.5 power-law in
equation (16) to
very small and large columns, the effective optical depth becomes an analytical
function of redshift and wavelength,
Due to the rapid increase with lookback time of the number of
absorbers, the mean free path of photons at 912 Å becomes so small
beyond a redshift of 2 that the radiation field is largely `local'.
Expanding equation (23) around z, one gets
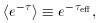
 forest clouds and LLS as a random
distribution of absorbers in column density and redshift space, then the
effective continuum optical depth of a clumpy IGM at the observed frequency
forest clouds and LLS as a random
distribution of absorbers in column density and redshift space, then the
effective continuum optical depth of a clumpy IGM at the observed frequency
 o for an observer at
redshift zo is
o for an observer at
redshift zo is
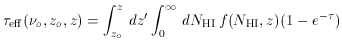
 =
NHI
=
NHI
 H(
H( ) is the hydrogen Lyman continuum optical
depth through an individual cloud at frequency
) is the hydrogen Lyman continuum optical
depth through an individual cloud at frequency
 =
=
 o (1 + z) / (1 +
zo).
This formula can be easily understood if we consider a situation in which
all absorbers have the same optical depth
o (1 + z) / (1 +
zo).
This formula can be easily understood if we consider a situation in which
all absorbers have the same optical depth
 0 independent of
redshift, and the mean number of systems along the path is
0 independent of
redshift, and the mean number of systems along the path is
 N =
N =
 dzdN /
dz. In this case the Poissonian probability of encountering a total
optical depth
k
dzdN /
dz. In this case the Poissonian probability of encountering a total
optical depth
k 0
along the line-of-sight (with k integer) is
p(k
0
along the line-of-sight (with k integer) is
p(k 0) =
e
0) =
e N
N
 Nk /
(
Nk /
( 0 k!), and
< e-
0 k!), and
< e- > =
e-k
> =
e-k 0
p(k
0
p(k 0) =
exp[-
0) =
exp[- N(1 -
e-
N(1 -
e- 0)].
0)].
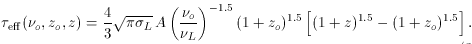
 eff
(
eff
( L)
L)
 0.36 (1 + z)2
0.36 (1 + z)2
 z. This means that at
z = 3, for
example, the mean free path for a photon near threshold is only
z. This means that at
z = 3, for
example, the mean free path for a photon near threshold is only
 z = 0.18, and sources of
ionizing radiation at higher redshifts are severely attenuated.
z = 0.18, and sources of
ionizing radiation at higher redshifts are severely attenuated.