Dwarf spheroidal galaxies

3.3 Dwarf spheroidal galaxies

This type of galaxy is probably the most common in the Universe. Despite their low luminosity, they may contain large amounts of dark matter, and thus contribute greatly to the mass of the Universe. However, dwarf spheroidals do not possess gas in the periphery, as do bright ellipticals. Therefore, the determination of DM is more problematic. There are basically two methods for detecting dark matter in this type of galaxies:

a) Tidal radii.- The dwarf spheroidal satellites of the Milky Way, for instance, could become tidally disrupted if they did not have enough dark matter, thus increasing autogravitation and preventing it. Let us determine the radius of the satellite necessary for autogravitation to match tidal disruption, by means of a rough model.

Suppose a satellite dwarf with mass m and radius r orbiting around the primary galaxy with mass M, with R being the distance between the two galaxies. Suppose the dwarf divided into two halves. They would attract one another with a force of the order of Gm²/r². The tidal disrupting force would be the difference in gravitational force produced by the primary ${{GMm}\over 2}$ $\left(\vphantom{ {1 \over {(R-r)^2}} - {1 \over {(R+r)^2}} }\right.$ ${1 \over {(R-r)^2}}$ - ${1 \over {(R+r)^2}}$ $\left.\vphantom{ {1 \over {(R-r)^2}} - {1 \over {(R+r)^2}} }\right)$ $\approx$ GMmr/r³. The two forces become equal when

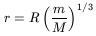
(27)

More precise calculations (e.g. Binney and Tremaine, 1987) give the same orders of magnitude. As the dwarf is not a rigid body, at a galactocentric radius equal to this critical value, r, stars would escape and would be trapped in the gravitational field of the primary. Therefore, at a "tidal radius", r, the density should drop to zero. From the observational point of view, the tidal radius is difficult to determine, and so it must be obtained by extrapolation. It seems to be too large, when m is obtained from the surface brightness with a constant M/L relation.

Hodge and Michie (1969) first detected a greater than expected tidal radius for Ursa Minor, and Faber and Lin (1983) first used this procedure for estimating dark matter. More (1996) used the observation of stars being removed in the tidal tails of dwarf galaxies to conclude that their dark matter halos must be truncated at 400 pc, limiting their M/L ratio to less than about 100. Burkert (1997) investigated four dwarf spheroidal galaxies orbiting around the Milky Way: Sextans, Carina, Ursa Minor and Draco, considering their tidal radii, and concluded that Sextans is dark matter dominated but not the other three.

It should be emphasized that the mass obtained depends on the third power of the estimated tidal radius, which is an important source of errors. On the other hand, what is actually estimated is the m/M ratio. If the Milky Way mass were overestimated, so would be the mass of the satellite. If the Milky Way contained no dark matter the satellite in turn would not require this component.

b) The velocity dispersion of the stellar system.- This method has much in common with that used for the central parts of other galaxies. But in others, the analysis is complemented with peripherical effects which are now completely absent. The study of the dark matter in dwarf spheroidals basically rests on the assumption that its distribution and that of the stars are similar, a condition which is probably unrealistic, unless this type of galaxy is the only exception. Nevertheless, most workers on this topic generally agree that these galaxies have a large DM content, maybe 10 times higher than luminous matter; indeed, ratios of 100 have been reported as well as very high central condensations in the range ( 0.1 - 1Mpc^-3) (Mateo et al. 1992).

The possibility that all dwarf galaxies may have the same mass, despite their large luminosity range, has been proposed (see Ashman, 1983). Mateo (1997) obtains a mass of 2 × 10⁷M for all dwarf spheroidals irrespective of their luminosity. Salucci and Persic (1997) obtain M $\propto$ L^1/4. Among the observational difficulties we should also mention the fact that velocity dispersions are low, of the order of 10 kms^-1, and therefore, a high spectral resolution is required.

If luminous and dark matter have the same spatial distribution, it is easy to deduce the central density and the central mass-to-luminosity ratio. From the Virial theorem, we straightforwardly deduce

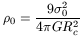
(28)

where $\rho_{0}^{}$ is the central density, $\sigma_{0}^{}$ the central velocity dispersion and R_c an equivalent radius, or core radius, identifiable with the radius at which the surface brightness is one half the central value. Within this radius, the mass would be $\rho_{0}^{}$ ${4 \over 3}$ $\pi$ R_c³ and the luminosity, $\Sigma_{0}^{}$ $\pi$ R_c², where $\Sigma_{0}^{}$ would be the observable central surface brightness. Hence, the M/L fraction would be

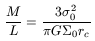
(29)

The constant should be 9/2 $\pi$ , instead 3/ $\pi$ , as deduced by more detailed calculations (Richstone and Tremaine, 1986; Ashman, 1993).

An important study was made by Kuhn and Miller (1989), in which dwarf spheroidal galaxies were not considered as virialized systems. These galaxies could be unbound and losing stars. Numerical simulations have been carried out by Kroupa (1997) and Klesen and Kroupa (1998) in which the dwarf satellites are partially disrupted in perigalactic passages; orbiting condensations can be identified after this event near the satellite. Then, they might contain no dark matter at all and yet present a high stellar velocity dispersion. The tidal disruption of a satellite produces a remnant that contains about 1% of the initial mass.

Summarizing, dwarf spheroidal galaxies could contain large amounts and concentrations of dark matter, but severe observational difficulties prevent their precise determination. Even models with no dark matter at all cannot be excluded.