
| (71) |



CDM models predict a halo structure which is responsible for the rotation curve of the spiral galaxies. Halo structures and rotation curves are therefore closely connected problems. Let us assume that halos are spherical.
Gunn and Gott (1972) concluded that the gravitational collapse could lead to the formation of virialized halos with almost isothermal profiles. A tempting assumption for the halo density distribution is therefore the so called non-singular "isothermal" sphere

| (71) |
defined with two parameters: the central density, ![]() , and the
core radius, Rc. In this isothermal profile
(d
, and the
core radius, Rc. In this isothermal profile
(d![]() /dR)(R = 0) = 0 and
/dR)(R = 0) = 0 and
![]() (R = 0) =
(R = 0) = ![]() is finite, two desirable properties for
a density profile. Out to
R
is finite, two desirable properties for
a density profile. Out to
R ![]() Rc, the density remains more or
less flat, i.e., there is a "core" of radius Rc. Note
that, in this case, the "circular velocity", V, is defined as
Rc, the density remains more or
less flat, i.e., there is a "core" of radius Rc. Note
that, in this case, the "circular velocity", V, is defined as

| (72) |
where M(R) is the mass in a sphere of radius R. It can then be deduced that the circular velocity is given by

| (73) |
which is an increasing function of R, asymptotically reaching
Vmax = V(R = ![]() ) given by
) given by

| (74) |
which might be an undesirable property (an asymptotically Keplerian curve would be preferable).
Other types of halos have been reviewed by Bertschinger (1998) and others. Recently Navarro, Frenk and White (1996, 1997) deduced from their CDM models that halos should be described by the so called "universal" or NFW profiles

| (75) |
where
![]() is the density of the critical Einstein-de Sitter
Universe
is the density of the critical Einstein-de Sitter
Universe

| (76) |
and ![]() , the characteristic contrast density
(dimensionless) and Rs,
the scale radius, are the parameters of the profile. It is singular,
, the characteristic contrast density
(dimensionless) and Rs,
the scale radius, are the parameters of the profile. It is singular,
![]() (R = 0) =
(R = 0) = ![]() , which is certainly an "unpleasant" property,
even if the mass M(0) converges. The NFW profile was called
"universal" because the authors found it in a large variety of halo
masses, spanning 4 orders of magnitude, from individual galaxies to
cluster halos, as well as for a large variety of cosmological
scenarios. Some authors (e.g.
Avila-Reese, Firmani and
Hernandez, 1998)
deduced that the density profile depends on the environment,
with the NFW appropriate only for isolated halos. The circular
velocity of this NFW halo can be calculated by
, which is certainly an "unpleasant" property,
even if the mass M(0) converges. The NFW profile was called
"universal" because the authors found it in a large variety of halo
masses, spanning 4 orders of magnitude, from individual galaxies to
cluster halos, as well as for a large variety of cosmological
scenarios. Some authors (e.g.
Avila-Reese, Firmani and
Hernandez, 1998)
deduced that the density profile depends on the environment,
with the NFW appropriate only for isolated halos. The circular
velocity of this NFW halo can be calculated by

| (77) |
where V200 is the circular velocity at
R200, called the
"Virial" radius. This virial radius is that radius for which
< ![]() > = 200
> = 200![]() , where <
, where < ![]() > is the mean density in a sphere of
radius R200.
Cole and Lacey (1996)
showed that this radius
approximately separates the virialized and infall regions. The
parameter c, called the concentration, is defined as
> is the mean density in a sphere of
radius R200.
Cole and Lacey (1996)
showed that this radius
approximately separates the virialized and infall regions. The
parameter c, called the concentration, is defined as

| (78) |
and is dimensionless. x is simply R/R200.
As
V2002 = GM200/R200 = G(200 × 3H2/8![]() G)(4
G)(4![]() (R200)3/3)/R200 = 100H02R2002, we have
V200 = 10H0R200, or
(R200)3/3)/R200 = 100H02R2002, we have
V200 = 10H0R200, or

| (79) |
if we measure V200 in kms-1 and R200 in kpc. Also:
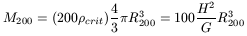
| (80) |
therefore
M200 ![]() R2003
R2003 ![]() V2003. If the
luminous mass were proportional to the halo mass,
M200, and if
Vopt were related to V200
(Vopt is the disk
velocity at Ropt, the optical radius), then a relation
similar to
the observational Tully-Fisher relation would be obtained. In conventional
astronomical units
V2003. If the
luminous mass were proportional to the halo mass,
M200, and if
Vopt were related to V200
(Vopt is the disk
velocity at Ropt, the optical radius), then a relation
similar to
the observational Tully-Fisher relation would be obtained. In conventional
astronomical units

| (81) |
where V200 is to be expressed in km/s. The
Tully-Fisher relation
clearly establishes a relation between the luminosity and some power of
the optical rotational velocity,
L ![]() Vopt3 or
L
Vopt3 or
L ![]() Vopt4. (The exponent
depends on the wavelength of the
observations. The higher value of 4 is for the infrared. See
van den Bosch (1999)
for a recent critical review).
Vopt4. (The exponent
depends on the wavelength of the
observations. The higher value of 4 is for the infrared. See
van den Bosch (1999)
for a recent critical review).
The obtention of the Tully-Fisher relation from the outcoming halo density distribution presents some problems. The slope obtained and the scattering of the points agree with the observations, but the theoretical curve is displaced with the observational curve (Frenk et al. 1997). Or equivalently, it is possible to vary the free parameters to match the Tully-Fisher relation but then the amplitude of the galaxy luminosity function is not matched. This is at present a failure of theoretical models. The number of predicted dark halos is excessive. Navarro, Frenk and White (1996) suggested several possibilities: other cosmological parameters, the existence of a large number of halos with no visible component, the non-detection of many existent low surface brightness galaxies, etc.
Even if the observational Tully-Fisher relation is basically reproduced, there is still no convincing explanation for the numerical outputs. As Navarro (1998) remarks: "Our analysis has made use of this surprisingly tight relation between disk luminosity and rotation speed but provides no firm clues to elucidate its origin".
There is a general argument based on
Shu (1982)
that does not explain the
Tully-Fisher relation but does introduce some light. If the total
luminosity of a galaxy is roughly
L ![]()
![]() Ropt2
(where
Ropt2
(where ![]() is the central surface brightness, notably the same
for all spirals, and Ropt the optical radius) and if
the total mass
within the optical radius is roughly
is the central surface brightness, notably the same
for all spirals, and Ropt the optical radius) and if
the total mass
within the optical radius is roughly
![]()
![]() RoptVopt2 (where Vopt is the asymptotic observed velocity) and
if
RoptVopt2 (where Vopt is the asymptotic observed velocity) and
if
![]() /L is roughly a constant, then
Ropt
/L is roughly a constant, then
Ropt ![]() Vopt2/
Vopt2/![]() . If
. If ![]() is really a constant
Ropt
is really a constant
Ropt ![]() Vopt2 and therefore
L
Vopt2 and therefore
L ![]() Vopt4. This argument
relies on the constancy of
Vopt4. This argument
relies on the constancy of ![]() , which so far has no explanation.
, which so far has no explanation.
The NFW circular velocity reaches a maximum at
R ![]() 2Rs =
2R200/c and declines beyond that radius. NFW
density profiles are
two-parametric and it is possible to choose V200 and
c to
characterize the halos, or the equivalent set of characteristic density
and halo
mass. A very exciting result of these theoretical models is that the two
free
parameters show a clear correlation. The reason behind this is that the
halo density reflects, and is proportional to, the true density when
the halo was formed, with the initial small halos being denser because they
formed earlier, when the density of the expanding Universe was higher.
But we also know that, due to the hierarchical halo
formation, more massive halos were born later. Then,
the existence of decreasing functions
2Rs =
2R200/c and declines beyond that radius. NFW
density profiles are
two-parametric and it is possible to choose V200 and
c to
characterize the halos, or the equivalent set of characteristic density
and halo
mass. A very exciting result of these theoretical models is that the two
free
parameters show a clear correlation. The reason behind this is that the
halo density reflects, and is proportional to, the true density when
the halo was formed, with the initial small halos being denser because they
formed earlier, when the density of the expanding Universe was higher.
But we also know that, due to the hierarchical halo
formation, more massive halos were born later. Then,
the existence of decreasing functions ![]() (t) and
M200(t)
implies a correlation between
(t) and
M200(t)
implies a correlation between ![]() (t) and
M200(t). Therefore,
in practice, rotation curves are intrinsically one-parametric.
Figure 18 plots the circular velocity curves
for different
values of the concentration, c. Low values of the concentration
parameters denote slowly rising curves, i.e. small ancient galaxies.
(t) and
M200(t). Therefore,
in practice, rotation curves are intrinsically one-parametric.
Figure 18 plots the circular velocity curves
for different
values of the concentration, c. Low values of the concentration
parameters denote slowly rising curves, i.e. small ancient galaxies.

|
Figure 18. NFW circular velocity profiles
for different values
of the concentration. The circular velocity at the virial radius,
V200, is chosen to match the rotation speed in the
outskirts of
the galaxy, and varies from 100 to 130 km s-1 from top to
bottom. As illustrated in this figure for NGC 3198, most galaxy
rotation curves can be adequately parametrized. The best fit value of
the c parameter (
cobs |
We saw above that the "maximum disk" hypothesis provides halo circular velocities. Do NFW halo profiles fit these profiles? Are disks really maxima? Do isothermal profiles provide a better fit than NFW profiles? A comparison of the theoretically predicted halos and the observations is necessary to answer these questions and to test the models. This comparison was made by Navarro (1998), who adopted about 100 disk galaxies from published observations and tried to deduce the NFW free parameter in each case. This analysis was also made under the isothermal halo assumption.
For this task, we should not forget that galaxies also have visible components, i.e. that spirals possess a disk and a bulge. For the surface brightness of the disk, Navarro (1998) assumed, as usual, an exponential disk

| (82) |
where
![]() =
= ![]() (R = 0) and Rd, the disk
radial scale
length, are two parameters. Exponential optical disks constitute a
reasonable zeroth-order description, but there is perhaps a misuse in
the literature, as above discussed. It is however an
appropriate and almost a necessary assumption in studies similar to that of
Navarro.
(R = 0) and Rd, the disk
radial scale
length, are two parameters. Exponential optical disks constitute a
reasonable zeroth-order description, but there is perhaps a misuse in
the literature, as above discussed. It is however an
appropriate and almost a necessary assumption in studies similar to that of
Navarro.
For the surface brightness of the bulge it is assumed that

| (83) |
where
![]() and Rb are two
parameters. Navarro assumed the
same M/L ratio in the bulge and in the disk, and taht this ratio was
another free parameter.
and Rb are two
parameters. Navarro assumed the
same M/L ratio in the bulge and in the disk, and taht this ratio was
another free parameter.
It is also usually assumed that the halo responds "adiabatically" to the growth of the disk (Barnes and White, 1984; Flores et al. 1993), which was also assumed by Navarro, Frenk and White (1996, 1997). This means a variation of the NFW profile within the disk region. Certainly, the formation of the disk must somewhat modify the halo density profile, probably in a way that is very difficult to model. This assumption was introduced in order to avoid disagreements with observations of the rotation of dwarf galaxies and therefore, as a correction of an initial theoretical failure. In fact, the rotation curve of dwarf galaxies indicates that the halo circular velocity rises almost linearly, which would mean a constant density (i.e. a halo core) in clear contradiction with the NFW profiles. As mentioned above, this hypothesis of the adiabatic response of the halo to the formation of the disk also alleviates the problem of the halo-disk conspiracy.
The results indicate that theoretical models must introduce a
higher degree of sophistication, because even isothermal profiles give
similar or
better results, specially for low surface brightness galaxies. Moreover,
observational rotation curves are very often well fitted by halos
with no disk and no bulge! This type of fitting is
meaningless, but Cosmology could benefit from it. The
concentration parameter, c, obtained after this peculiar
halo-only fitting
provides an upper limit which can be compared with the theoretical
predictions on c. The standard CDM model in general predicts higher
concentrations than the upper limits obtained. Therefore, if the
theoretical models are considered an efficient basis to interpret the
observations, then cosmological models with small
![]() (
( ![]() 0.3)
and large
0.3)
and large
![]() (
( ![]() 0.7) are favoured.
0.7) are favoured.
A puzzling observation within the DM interpretation of rotation curves
is the absence of correlation between the asymptotic velocity of disks
and the orbital velocity in binary systems. If the asymptotic velocity,
Vrot, is found in a region dynamically dominated by
the halo, and
the orbital velocity, Vorb, of a galaxy considered the
secondary
would, clearly, reflect the total mass of the primary,
Vrot and Vorb should correlate.
Navarro (1998)
seeks the explanation
in his Fig. 19 (top-right:
logV200 versus
logVrot).
If we observe the solid line in this figure, we see
that disks with
Vrot![]() 150kms-1 have
V200 > Vrot and
disks with
Vrot > 150kms-1 are all predicted
to have similar halo velocities,
V200
150kms-1 have
V200 > Vrot and
disks with
Vrot > 150kms-1 are all predicted
to have similar halo velocities,
V200 ![]() 200kms-1. Then, disk-dominated
galaxies would be surrounded by halos of approximately the same mass.
200kms-1. Then, disk-dominated
galaxies would be surrounded by halos of approximately the same mass.
This explanation of rotation curves remains incomplete. Samples do not contain dwarf galaxies. The Navarro sample is probably also lacking early bulge-rich galaxies. In Fig. 26 there are two other curves, the M/L =h curve and the varying M/L curve, which are not unreasonable (for instance, Vrot = V200 implies very small variations of M/L) but which, however, do not imply the same conclusion. Even if the solid line shows us a change in slope, the increasing function does not firmly predict the complete absence of correlation. The discussion of Navarro concerning this point is very illustrative but the puzzling behaviour of binary galaxies is not completely cleared up. The existence of an upper limit of the halo mass needs further justification.
Furthermore, Navarro and Steimetz (1999) find it difficult to reconcile the theory with data for the Milky Way and with the Tully-Fisher relation; they consider that substantial revision of the theoretical models is needed.
As a general conclusion, observational rotation curves are not incompatible with NFW halos, but the confrontation seems somewhat discouraging. We have examined the work of Navarro (1998) in some detail because it is probably the most serious and complete study linking the observed properties and the model outputs for rotation curves. However, either the observations do not constitute a proof of the CDM models, or dynamic ingredients other than halo and disk density profiles are necessary to study the rotation of spirals. Considering the success of the models in explaining and predicting other observational facts, we would suggest this second possibility as more plausible. In particular, we will later argue that ignoring magnetic fields in the interpretation of the rotation curves could be unrealistic.