2.4 The "Universal rotation curves"

Persic, Salucci and Stel (1996) and Salucci and Persic (1997) have analyzed a large number of rotation curves mainly catalogued by Persic and Salucci (1995) taking into account the H$\alpha$ data published by Mathewson, Ford and Buchhorn (1992) and also adopting some radio rotation curves. They claim that rotation curves can be fitted to what they call the "universal rotation curve" not only for any luminosity, but also for any type of galaxy, including spirals, low-surface-brightness, ellipticals and dwarf irregular galaxies. The existence of a "universal" rotation curve had previously been claimed by Rubin et al. (1980). Let us then reproduce the formulae of these "universal rotation curves", or PSS curves, restricting ourselves to spirals.

Following Persic and Salucci (1997), rotation curves of spirals can be fitted by a combination of two components. The first is an exponential thin disk, whose circular velocity can be approximated in the range 0.04R_opt < R$\le$2R_opt as

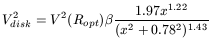
(3)

where x is a radial variable taking R_opt as unit

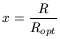
(4)

R_opt is the radius encircling 83% of the light; for an exponential disk R_opt = 3.2R_D where R_D is the radial scale length. $\beta$ is a constant that depends on the luminosity. This function V_disk does not give a Keplerian fall-off for x $\rightarrow$ $\infty$, nor is it the general expression of V_disk for exponential disks, but its application is restricted to a radial range.

The other component is the halo, with a circular velocity expressed as

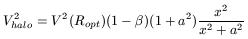
(5)

where a is another constant, also depending on the luminosity. Then, the PSS curve is given by

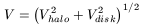
(6)

the contribution of a bulge therefore being considered negligible. The constants a and $\beta$ are functions of the galaxy's luminosity, the best results being obtained for

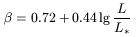
	(7)
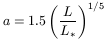
	(8)

where L_* = 10^10.4L_$\odot$. Then for a galaxy with luminosity L_*, a corresponds to a value of x of the order of R_opt, exactly 1.5R_opt. Note that these values provide good fits, but for L > 4.33L_* give negative values of V_halo².

Hence

(9)

(for a spherically symmetric halo) and

(10)

with very little in common with the NFW theoretical halos (see later). They are reasonable, because

• The x-derivative of $\rho$(x) vanishes at x = 0, which is physically satisfactory.

• Then, for x $\ll$ a the density slowly decreases; for x = a, the density is still 1/3 of the central value, i.e. there is a "core" of radius a, which is therefore called the halo core radius.

• The density does not vanish for any value of x, i.e. there is no sharp boundary. The density always decreases.

• For x $\gg$ a, the density decreases as x^-2 (compared to x^-3 in NFW halos).

This is reminiscent of the non-singular isothermal sphere, with a faster decrease from the centre out to the core radius, both of which for large x obey $\rho$ $\propto$ x^-2.

As a $\propto$ L^1/5, i.e. low luminosity galaxies are much more concentrated. For a galaxy with L_* the core is of the order of the optical radius.

A non-physical property of the PSS halo density profile is that M does not converge for very large values of x, but rather linearly increases with x, with the mass of any halo being infinite. To surmount this difficulty the halo mass was defined as that at R₂₀₀, where R₂₀₀ is the radius of a sphere within which the mean density is 200 times the mean density of the Universe, as also defined in theoretical models. Then

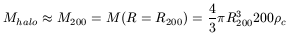
(11)

where $\rho_{c}^{}$ is the critical density of the Universe. We see therefore that M₂₀₀ $\propto$ R₂₀₀³. Following equation (5), V₂₀₀ (the circular velocity at R₂₀₀) is a complicated function of R₂₀₀, but according to these authors, it can be approximated to

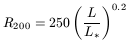
(12)

As the exponent, 0.2, is very small, the radii of the halos are relatively independent of the luminosity. A galaxy with 10L_* would have a halo only 1.5 times larger than a galaxy with luminosity L_* (this cannot be checked directly as also equation (5) cannot be applied to galaxies with L > 4.33L_*). The authors propose

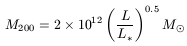
(13)

(Note, however, that from R₂₀₀ $\propto$ L^0.2, together with the exact relation M₂₀₀ $\propto$ R₂₀₀³, we should obtain M₂₀₀ $\propto$ L^0.6. The small difference in these exponents -0.5 and 0.6- arises from the complexity of the problem). Therefore, the brighter galaxies have a halo that is more massive, but only slightly larger. The mass-luminosity ratio is then

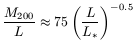
(14)

Brighter galaxies have smaller mass-to-light ratios, hence the dark matter has more dominant effects in small or low-surface brightness galaxies. We can also calculate the luminous to dark matter ratio

(15)

Bright galaxies have relatively smaller dark matter halos, while the very bright galaxies nearly reach the maximum M_lum/M_dark ratio ($\sim$ 0.1) established from primordial nucleosynthesis models for the baryonic $\Omega_{B}^{}$.

For x $\gg$ a, a constant value of V_halo is obtained V_halo² = V²(R_opt)(1 - $\beta$)(1 + a²). For galaxies with L $\sim$ L_*, it is obtained that V₂₀₀ $\sim$ V(R_opt) which is readily interpreted: if a constant V(R_opt) is observed in a region already dominated by dark matter, it should be related to the halo circular velocity at large distances.

As V²₂₀₀ = GM₂₀₀/R₂₀₀ $\propto$ L^0.5/L^0.2 = L^0.3 we should have V₂₀₀ $\propto$ L^0.15. In binary galaxies, which are considered later, V₂₀₀ could be identified with the orbital velocity of the secondary galaxy, statistically related to the difference of the two projected velocities along the line-of-sight. L would be the luminosity of the primary. A correlation between L and V₂₀₀ has not been found (e.g. Zaritsky, 1997). This is, in part, justified as the exponent, 0.15, is so small that the orbital velocities are nearly independent of the luminosities. Theoretical models also agree in this respect.

Note that, if instead of M₂₀₀ $\propto$ L^0.5 as determined by these authors, we had taken M₂₀₀ $\propto$ L^0.6 from the definition of M₂₀₀ as mentioned above, we would have obtained V₂₀₀ $\propto$ L^0.2, and L $\propto$ V⁵₂₀₀, closer to the observational infrared Tully-Fisher relation L $\propto$ V⁴(R_opt), if V(R_opt) were close to V₂₀₀.

White et al. (1983) and Ashman (1992) proposed M₂₀₀/L $\propto$ L^-3/4, in which case R₂₀₀ $\propto$ L^0.08, indicating a lower dependence of R₂₀₀ on L, and V₂₀₀ $\propto$ L^0.08. We will see later that these undetected correlations have a natural explanation in the magnetic model of the rotation curves.

The universal rotation curves also give two relations

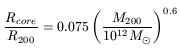
	(16)
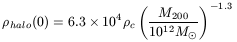
	(17)

where $\rho_{c}^{}$ is the critical density of the Universe. Hence, brighter galaxies have relatively large core radii and small values for the central halo density. Therefore, even the central region of low-brightness galaxies is dominated by dark matter, while bright galaxies have their internal regions dominated by visible matter. These relations are important and confirmed by the NFW theoretical halos, even if the universal rotation curves do not have much in common with those deduced by the former.

The same formulae are valid for low-surface-brightness galaxies. In this case, the dark matter would be completely dominant, with a core radius of about 5-6 kpc.

Summarizing, the most interesting fact in the fitting effort made by these authors is that such a large variety of galactic types have rotation curves which can be adjusted to a single universal rotation curve (even for ellipticals, not considered here). This fitting assumes the existence of a dark halo that does not coincide with the universal halo profiles obtained by most theoretical models but which is very reasonable (except, perhaps, in that they have an infinite mass, which in practice is not a real problem). The explanation of the puzzling behaviour of binary systems, however, is still not completely satisfactory.

There is another general comment to be made. The universal rotation curve is a fitting problem. But this fitting should be interpreted in other models in a different way. Therefore, even if terms like "dark matter" and "dark halos" are used, this fitting does not prove the existence of dark matter in galaxies.

Bosma (1998) considered that the notion of universal rotation curves breaks down. He observed several galaxies with a high rotation velocity, but non-declining rotation curves. This could be due to the inclusion in Persic and Salucci's sample of very inclined galaxies, where opacity problems are difficult to handle when using H_$\alpha$ rotation curves. Verheijen (1997) also found 10 out of 30 galaxies in the Ursa Major clusters for which the rotation curves do not fit the universal rotation curves. Despite all these exceptions the scheme introduced by Persic, Salucci and collaborators, provides a first fit that theoretical models should take into account.