2.6 The rotation curve of the Milky Way

Paradoxically, the rotation curve of the nearest galaxy remains poorly known. Extinction is too large to observe the stars and too small to observe the gas. It is preferable to observe the gas, either at 21 cm or at 2.7 mm, because it extends at much greater radii. Thus we must rely on the corotation of both the stellar and the gaseous systems, an assumption that is not always justified, as mentioned previously. The tangent-point method to obtain the rotation curve for R < R₀, with R₀ being the solar galactocentric distance, is well known and need not be repeated here in detail.

The points of the circle with a Galactic Centre-Sun diameter are characterized by a radial velocity from the Sun equal to their rotation velocity, and this velocity is determined by the fact that it corresponds to the largest redshift (in the first quadrant) or the largest blueshift (in the fourth quadrant). The different values at the points of this circle give us the rotation curve.

However, this method only provides the rotation curve out to 8 kpc, but to analyze our dark halo and the mass of the Milky Way itself, this is too small. To extend the rotation curve to larger galactocentric distances, a variety of objects have been observed. These objects have to be bright, to be observed from afar, their distance must be accurately determined (which in practice is the largest source of error) and their radial velocities must be easily obtainable. Carbon stars, OB stars, planetary nebulae, cepheids and HII regions have been used to study the outer Galaxy, but the errors are large and the maximum distance is less than 2R₀. A complete account of these attempts was given in the review by Fich and Tremaine (1991) and will not be repeated here. There is a crucial date (1965) prior to which, as reviewed by Schmidt (1965), it was thought that the outer rotation curve was Keplerian and the estimated mass of the Milky Way was about 2 × 10¹¹M_$\odot$. After this year, various authors began to realize that the outer curve was more or less flat, and the conclusion that our Milky Way may contain large amounts of dark matter became more and more widely accepted.

The best method to investigate the outer rotation curve was proposed by Merrifield (1992), who considered that a ring in the Milky Way with constant vertical scale length, h_z, has a variable angular size when seen from the Sun; or in his own words "much as a person standing in a volcano might estimate his or her location within the crater from the variations in the apparent height of the walls in different directions". It is easily obtained that

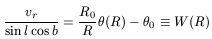
(22)

where v_r is the radial velocity from the Sun, $\theta$(R) is the rotation at a point with galactocentric distance R, $\theta_{0}^{}$ is the rotation velocity at R = R₀ and l and b are the galactic longitude and latitude. Therefore, if we have a data cube T_b(v_r, l, b), where T_b is the HI brightness temperature, it is possible to divide the cube into slices with constant W(R) as defined in the above equation. W(R) only depends on R and we may use h_z to know exactly what value of R we are speaking about. From our location in the Galaxy, the HI layer of thickness h_z at some point of radius R will present an angular size in galactic latitude of

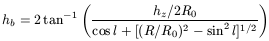
(23)

If we then take a constant-W slice, obtain the variation in angular width as a function of longitude l, and compare it by this formula, we can calculate it by fitting the value of R/R₀ (and even h_z/R₀) of the slice, and hence obtain v_r(R/R₀) and h_z(R/R₀).

There are some inherent problems. The orbits must be circular and vertical shear must be absent, i.e. v_r should not depend on z. The galactic warp introduces further complications, although these can be overcome. In such a way, Merrifield was able to reach points in the Milky Way rotation curve out to about 20 kpc, or 2.5 R₀, with an unprecedented degree of precision.

The results greatly depend on the values of R₀ and $\theta_{0}^{}$. Merrifield proposed R₀ = 7.9$\pm$0.8kpc and $\theta_{0}^{}$ = 200$\pm$10kms^-1, rather lower than usually recommended in other works, to match other kinematic constraints and in line with the rotation curves of similar galaxies. More recently, Honma and Sofue (1996, 1997) have used Merrifield's method to estimate the rotation curve, the geometry of the halo and the total mass of the Milky Way, investigating their uncertainties. Errors in R₀ are relatively unimportant because they just change the scaling in the radial direction, but changes in $\theta_{0}^{}$ produce highly different interpretations of our hypothetical halo. In Fig. 11 we plot their results for three different values of $\theta_{0}^{}$: 220, 200 and 180 km s^-1.

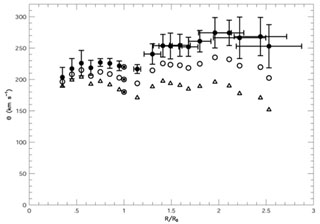
Figure 11. Overall rotation curves of the Galaxy for $\theta_{0}^{}$ = 220kms^-1 (filled circles), $\theta_{0}^{}$ = 200kms^-1 (open circles), and $\theta_{0}^{}$ = 180kms^-1 (open triangles). The data for the inner rotation curve were taken from Fich et al. (1989). The outer rotation curve are those obtained by Merrifield's method. The error bars are indicated only for $\theta_{0}^{}$ = 220kms^-1, and are almost the same for the three cases. From Honma and Sofue (1997). Courtesy of the Astronomical Society of Japan.

The rotation velocity decreases beyond 2R₀ for all cases. Reasonable Keplerian fits are obtained for R$\ge$2R₀ if $\theta_{0}^{}$ is in the range 200-207 kms^-1. If $\theta_{0}^{}$ < 200kms^-1 the curve declines faster than Keplerian.

Using $\theta_{0}^{}$ = 220kms^-1, as recommended by the IAU, the outer rotation curve rises between R = 1.1R₀ and 2R₀, which is uncommon in other galaxies of the same type, having a flat curve within the optical disk. To obtain a flat rotation curve, $\theta_{0}^{}$ should be as small as 192 km/s.

R₀ and $\theta_{0}^{}$ are related to Oort's constants A and B (note A - B = $\theta_{0}^{}$/R₀), which are fairly well determined. ( $\theta_{0}^{}$/R₀ could also be directly determined by means of the VLBI determination of the proper motion of Sgr B2, taking two quasars behind as reference. Accurate data, in this respect, will be available in the near future. Honma and Sofue (1996) propose $\theta_{0}^{}$ = 200km and therefore R₀ = 7.6kpc, based on this result and those obtained by other authors also claiming lower $\theta_{0}^{}$ and R₀.

Assuming a spherical mass distribution they obtain for the mass of the Milky Way a low value of 2.0$\pm$0.3 × 10¹¹M_$\odot$, which is close to the early estimates.

The Keplerian rotation curve does not require dark matter beyond 2R₀, but it would still be necessary within 2R₀, because an exponential disk has a rotation curve declining beyond 2.2r, when r is the radial scale length, in conflict with the flat rotation out to 2R₀. However, the dark matter needed could be much less than previously calculated. On the other hand, the shape of the dark halo would differ greatly from that theoretically deduced.