The universally high abundance of helium in stars and nebulae, Y
0.24, is considered to
be one of the fundamental pieces of evidence in favor of the "standard"
hot big-bang
cosmological model. Calculations of nucleosynthesis in the early
universe show that the
helium to hydrogen abundance ratio is a function of several fundamental
cosmological and
physical parameters: the baryon to photon number ratio, number of
neutrino families, and neutron half-life (e.g.
Yang et al. 1984).
Metal-poor H II regions, where nucleosynthetic
activity and enrichment by stars has been minimal, offer extremely
attractive sites for
attempting to determine the primordial helium fraction
YP. This realization has led to many
attempts to measure helium abundances as precisely as possible for
extragalactic H II
regions. There are many thorough reviews of these efforts and their
results in the
astronomical literature; these include the proceedings of the 1983 ESO
conference on helium abundances
(Shaver, Kunth, and
Kjär 1983),
and more recent reviews by
Shields (1986),
Boesgaard and Steigman
(1985),
and Kunth (1986).
In the following discussion,
I emphasize the uncertainties and problems in determining YP;
the interested reader may consult the above references for further details.
A great deal of excitement was generated about ten years ago by the announcement of anomalously low helium values derived from several extragalactic H II regions, YP < 0.22, by French (1980), French and Miller (1981), Rayo, Peimbert, and Torres-Peimbert (1982). Such low values presented a conundrum for cosmological models. However, the disagreement was significant only if the observational errors were substantially smaller than 10%, prompting further studies to re-examine the question. Kunth and Sargent (1983) studied a sample of about a dozen metal-poor H II regions, and took the average value of measured Y in this sample as being representative of the primordial value, i.e. YP = 0.245, which was not in conflict with the standard model. Nevertheless, since helium can be presumably be added but not removed by stellar activity, the existence of any H II region with a helium fraction less than a cosmologically "allowed" value would seem to disprove the simple big-bang model. The profound consequences of establishing a truly low value of Y in H II regions motivated a number of authors to pursue the issue further.
5.2. Demands on the Observations
5.2.1. Corrections to the Line Intensities. In order to definitively establish whether there is a conflict with standard cosmologies, it is necessary to determine the He/H ratio with a precision and accuracy which is unprecedented for astronomical determinations of chemical abundances. Therefore, it becomes essential to consider and correct for every possible source of observational uncertainty, including many effects that can usually be ignored in other contexts. Extensive discussions of the uncertainties involved in determining He/H values in extragalactic H II regions have been given by Davidson and Kinman (1985) and Dinerstein and Shields (1986), in the context of detailed studies of particular objects. Some of the most interesting galaxies (I Zw 18, for example) are so faint that achieving the necessary signal-to-noise in the helium line intensity measurements is a challenge, at least for the present generation of large telescopes (of apertures of 3 to 5 m). Going beyond such standard considerations, several other issues have been raised in the course of pursuing the helium problem. For example, most of the measurements of He/H in the literature were made with IDS (image dissector-scanner) instruments, which have been found to display slight non-linearities in the relationship between counts and flux. This non-linearity, while unimportant under most circumstances, becomes very important in the case of helium. Several different values have been proposed for the magnitude of this effect (e.g. Rosa 1985; Peimbert and Torres-Peimbert 1987); perhaps different individual instruments do indeed have different non-linearities. The issue may become moot, with IDS systems being replaced by CCDs, although the burden of proving the linearity of instruments will remain if the results are to be believed to the percent level.
Another problem affects only He I 5876Å, generally the strongest helium line observed, and therefore given more weight than other measured He I lines. For objects with small positive redshifts (which includes most of the key extragalactic H II regions), 5876Å shifts to the vicinity of the Na I lines at 5889, 5895Å. While telluric emission in the Na I lines can be removed by sky subtraction, it is not so easy to compensate for absorption by Na I in our own Galaxy, an effect which can be at least as large as 10-15% (Davidson and Kinman 1985; Davidson, Kinman, and Friedman 1989). Higher spectral resolution can help somewhat with this problem. Yet another factor which influences the He I line intensities is collisional excitation out of metastable levels. This concern was raised recently by Ferland (1986), who claimed that it could be a large effect; a reassessment by Clegg (1987), using newer calculations of the relevant cross-sections, found the effect on the derived helium abundances to be minor.
In many cases, the entrance aperture for the nebular observations
includes not only ionized gas, but also continuum from the ionizing
stars (see Section 1.2.). In the spectra of
hot stars, the hydrogen and helium lines will be in absorption. Since
these observations are
generally made with spectral resolutions too low to resolve the narrower
emission lines
from the underlying absorption features, the emission line intensities
will be weakened
accordingly. However, unlike the emission decrement, the absorption line
decrement is
fairly flat; thus, given three or more hydrogen lines, it is possible to
solve simultaneously
for both interstellar reddening and the strengths of the absorption
lines (e.g.
Rayo, Peimbert, and
Torres-Peimbert 1982;
McCall, Rybski, and
Shields 1985).
In general, the
emission equivalent widths of the first few hydrogen recombination lines
(H
,
,
Dinerstein and
Shields 1986).
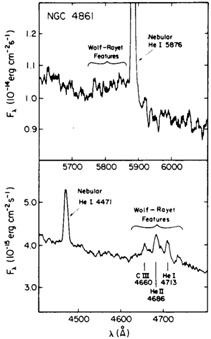
The problem of correcting for underlying absorption H and He absorption features in the hot star photospheres is not the only problem introduced by the stellar continuum. As discussed in Section 1.4., it is becoming apparent that many extragalactic H II regions contain Wolf-Rayet stars. Such stars produce broad, complex emission features, one of which falls near He I 5876Å. Figure 8 shows this spectral region as well as the region near He II 4686Å, for the dwarf irregular NGC 4861 (Dinerstein and Shields 1986). It is apparent from the figure that, unless one knows the intrinsic shape of the underlying continuum (i.e. whether there is net emission or absorption from the stars), there will be a substantial uncertainty in the strength of the nebular He I 5876Å line. Unfortunately, at present one cannot do much better than to guess at the continuum shape, since the Wolf-Rayet features in extragalactic H II regions display a variety of shapes (D'Odorico, Rosa, and Wampler 1983, and references given above). The best prospect for measuring accurate He I 5876Å lines is to avoid using apertures which contain starlight.
|
Figure 8. Two segments of the spectrum of the dwarf irregular galaxy NGC 4861 containing Wolf-Rayet emission features are shown. The upper panel shows how these features interfere with the measurement of nebular He I 5876Å. (Figure from Dinerstein and Shields 1986). |
5.2.2. The Correction for Neutral Helium. So far we have discussed only the uncertainties in determining the ionic ratio He+ / H+. As with derivations of metal abundances, it is necessary to take into consideration the relative fractions of each element in the observed ions, in order to obtain the elemental abundance ratio. Of the other ions of helium, He++ produces visible recombination lines, primarily 4686Å. This line has been seen in several extragalactic H II regions, but there is some difficulty in distinguishing whether it arises from the nebula or from Wolf-Rayet stars; a true nebular emission line of He II would require the presence of at least some UV radiation from extremely hot stars (e.g. Rayo, Peimbert, and Torres-Peimbert 1982; Dinerstein and Shields 1986). However, even if nebular in origin, He++ represents only a couple of percent of the total helium abundance.
Neutral helium is a potentially much larger component, and, furthermore,
it cannot be
observed directly. The neutral helium fraction is presumably minimized
in nebulae with a
high degree of ionization, which, as mentioned above, is usually the
case for H II regions with low metal abundances. However, it is still
necessary to understand how much neutral
helium might be present. Some workers have employed empirical ionization
correction formulae for this correction; others have used nebular ionization
models. One interesting point is that for T*
40,000 K, the He+ Strömgren sphere actually extends
further out than that for H+; therefore the ionization
correction factor is less than 1, but only by a few
percent at most: He/H 
0.98 × [He+ / H+]
(Stasinska 1980;
Shields and Dinerstein
1986).
On the other hand, it is very difficult to establish that a particular
nebular ionization model
is a unique solution for an observed set of line
intensities. Particularly for distant objects,
there is always the possibility that one is observing several spatially
distinct regions which
are not resolved by the spectrophotometric measurements. In this case,
it is possible for
there to be a large amount of neutral helium "hidden" inside separate
low-ionization nebulae
ionized by cooler stars. Such "composite" models have been examined, for
example, by
Dinerstein and Shields
(1986)
and Peña
(1986),
who find that the correction for neutral
helium could easily be as great as 10% in this case.
5.2.3. The Correction for Stellar Synthesis. There remains the
question of whether or not
to attempt to correct for the presumed contribution of helium
synthesized by stars. It has
been suggested that this contribution should be related linearly to the
amount of heavier
elements synthesized by the same stars or at least the same population
of stars. If such a
relationship can be established and the value of
Y /
Z determined, then any measured
helium abundance can be extrapolated backwards to obtain
YP. The problem is that there is
no general agreement on the value of this coefficient. Estimates for
Y / Z have varied from 1.7
(Lequeux et al. 1979)
to 5.7
(Pagel, Terlevich, and
Melnick 1986).
Others tend to take a value of around 3
(Rayo, Peimbert, and
Torres-Peimbert 1982).
Meanwhile,
Kunth and Sargent
(1983),
among others, have argued that there is no such correlation
between Y and Z, within the low-metallicity domain. There is also the
question of how one
determines "Z". Originally it was calculated from O/H, but more recently
many authors
have suggested calculating the stellar helium contribution from the
abundances of N or C,
the rationale being that the sites of helium synthesis are also sources
N and/or C (e.g.
Pagel 1985;
Vigroux, Stasinska,
and Comte 1987;
Steigman, Gallagher,
and Schramm 1989;
Torres-Peimbert,
Peimbert, and Fierro 1989).
5.3. Current Status and Future Prospects
The current situation is that various groups have estimated the value of
the primordial helium abundance to fall in the range 0.23
YP
0.24
(Torres-Peimbert,
Peimbert, and Fierro 1989;
Pagel and Simonson
1989).
This is uncomfortably close to the lower limit for
the standard cosmological model, but not in actual direct conflict with
it (although it does
rule out the possible existence of unknown families of
neutrinos). However, there is still
essentially no decisive proof of the existence of actual, as
opposed to extrapolated, helium
abundances lower than Y = 0.24. There is also no substantial evidence
for variations in the primordial abundance from place to place (see
Dinerstein and Shields
1986).
In view of the
caveats discussed in the last section, it seems clear that it is not
going to be easy to improve
on the current situation. The Hubble Space Telescope will at least
provide better
opportunities to measure the nebular spectrum without contamination by
stellar continuum.
It may also help with the correction for neutral helium, because it may
be possible to
spatially resolve the nebular ionization structure. However, the
question of the correction
for stellar-synthesized helium will remain. Thus, unless an actual,
present-day, helium
abundance lower than permitted by the standard cosmology is found, there
probably will
continue to be controversy about any further inferences regarding the
primordial value.