Published in "Observational Evidence for the Black Holes
in the Universe", Conference held in Calcutta, January 11-17th, 1998.,
p. 157
SUPERMASSIVE BLACK HOLES IN GALACTIC NUCLEI
Observational Evidence and Some Astrophysical Consequences
Luis C. Ho
Harvard-Smithsonian Center for Astrophysics
60 Garden St., Cambridge, MA 02138, USA
Abstract.
I review the status of observational determinations of central masses in
nearby galactic nuclei. Results from a variety of techniques are
summarized,
including ground-based and space-based optical spectroscopy, radio VLBI
measurements of luminous water vapor masers, and variability
monitoring studies of active galactic nuclei. I will also discuss recent
X-ray observations that indicate relativistic motions arising from the
accretion disks of active nuclei. The existing evidence suggests that
supermassive black holes are an integral component of galactic structure,
at least in elliptical and bulge-dominated galaxies. The black hole mass
appears to be correlated with the mass of the spheroidal component of the
host galaxy. This finding may have important implications for many
astrophysical issues.
Table of Contents
 MOTIVATION
MOTIVATION
 EARLY CLUES FROM PHOTOMETRY
EARLY CLUES FROM PHOTOMETRY
 METHODS BASED ON STELLAR KINEMATICS
METHODS BASED ON STELLAR KINEMATICS
 METHODS BASED ON GAS KINEMATICS
METHODS BASED ON GAS KINEMATICS
 Optical Emission Lines
Optical Emission Lines
 Radio Spectroscopy of Water Masers
Radio Spectroscopy of Water Masers
 Determining Central Masses of Active Galactic
Nuclei
Determining Central Masses of Active Galactic
Nuclei
 INDIRECT, BUT TANTALIZING EVIDENCE
INDIRECT, BUT TANTALIZING EVIDENCE
 ARE THE MASSIVE DARK OBJECTS REALLY BLACK
HOLES?
ARE THE MASSIVE DARK OBJECTS REALLY BLACK
HOLES?
 THE BLACK-HOLE MASS/BULGE MASS RELATION
THE BLACK-HOLE MASS/BULGE MASS RELATION
 ARE SUPERMASSIVE BLACK HOLES UBIQUITOUS?
ARE SUPERMASSIVE BLACK HOLES UBIQUITOUS?
 SOME IMPLICATIONS AND FUTURE DIRECTIONS
SOME IMPLICATIONS AND FUTURE DIRECTIONS
 REFERENCES
REFERENCES
1.MOTIVATION
The discovery of quasars in the early 1960's
quickly spurred the idea that these amazingly powerful sources derive their
energy from accretion of matter onto a compact, extremely massive object,
most likely a supermassive black hole (SMBH;
Zel'dovich & Novikov
1964;
Salpeter 1964;
Lynden-Bell 1969)
with M  106 - 109
M
106 - 109
M . Since then this
model has provided a highly useful framework for the study of quasars, or
more generally, of the active galactic nucleus (AGN) phenomenon
(Rees 1984;
Blandford & Rees 1992).
Yet, despite its success, there is little empirical
basis for believing that this model is correct. As pointed out by
Kormendy & Richstone
(1995,
hereafter KR), our confidence that SMBHs must power AGNs
largely rests on the implausibility of alternative explanations. To be
sure, a number of characteristics of AGNs indicate that the central
engine must be tiny and that relativistic motions are present. These
include rapid X-ray variability, VLBI radio cores, and superluminal
motion. However,
solid evidence for the existence of SMBHs in the centers of galaxies has,
until quite recently, been lacking.
. Since then this
model has provided a highly useful framework for the study of quasars, or
more generally, of the active galactic nucleus (AGN) phenomenon
(Rees 1984;
Blandford & Rees 1992).
Yet, despite its success, there is little empirical
basis for believing that this model is correct. As pointed out by
Kormendy & Richstone
(1995,
hereafter KR), our confidence that SMBHs must power AGNs
largely rests on the implausibility of alternative explanations. To be
sure, a number of characteristics of AGNs indicate that the central
engine must be tiny and that relativistic motions are present. These
include rapid X-ray variability, VLBI radio cores, and superluminal
motion. However,
solid evidence for the existence of SMBHs in the centers of galaxies has,
until quite recently, been lacking.
As demonstrated by
Soltan (1982),
simple considerations of the quasar
number counts and standard assumptions about the efficiency of energy
generation by accretion allows one to estimate the mean mass density of
SMBHs in the universe. The updated analysis of
Chokshi & Turner (1992)
finds 

 2 ×
105
2 ×
105 0.1-1
M
0.1-1
M Mpc-3
for a radiative efficiency of
Mpc-3
for a radiative efficiency of
 =
0.1
=
0.1 0.1.
Comparison of
0.1.
Comparison of 
 with the B-band galaxy luminosity density of
1.4×108h
L
with the B-band galaxy luminosity density of
1.4×108h
L Mpc-3
(Lin et al. 1996),
where the Hubble constant
H0 = 100h km s-1 Mpc-1,
implies an average SMBH mass per unit
stellar luminosity of ~ 1.4×10-3
Mpc-3
(Lin et al. 1996),
where the Hubble constant
H0 = 100h km s-1 Mpc-1,
implies an average SMBH mass per unit
stellar luminosity of ~ 1.4×10-3
 0.1-1h-1
M
0.1-1h-1
M /
L
/
L . A typical bright
galaxy with LB*
. A typical bright
galaxy with LB*
 1010h-2
L
1010h-2
L potentially
harbors a SMBH with a mass
potentially
harbors a SMBH with a mass
 107
107 0.1-1 h-3
M
0.1-1 h-3
M . These very general
arguments lead one to conclude that "dead" quasars ought to be lurking
in the centers of many nearby luminous galaxies.
. These very general
arguments lead one to conclude that "dead" quasars ought to be lurking
in the centers of many nearby luminous galaxies.
The hunt for SMBHs has been frustrated by two principal limitations. The
more obvious of these can be easily appreciated by nothing that the "sphere
of influence" of the hole extends to
rh  GM
GM /
/
 2
(Peebles 1972;
Bahcall & Wolf 1976),
where G is the gravitational constant and
2
(Peebles 1972;
Bahcall & Wolf 1976),
where G is the gravitational constant and
 is the velocity dispersion
of the stars in the bulge, or, for a distance of D, ~ 1"
(M
is the velocity dispersion
of the stars in the bulge, or, for a distance of D, ~ 1"
(M / 2
× 108
M
/ 2
× 108
M )(
)( / 200 km
s-1)-2(D/5 Mpc).
Typical ground-based observations are therefore severely hampered by
atmospheric seeing, and only the heftiest dark masses in the closest
galaxies can be detected. The situation in the last few years has improved
dramatically
with the advent of the Hubble Space Telescope (HST) and radio VLBI
techniques. The more subtle complication involves the actual modeling
of the stellar kinematics data, and in this area much progress has also
been made recently as well.
/ 200 km
s-1)-2(D/5 Mpc).
Typical ground-based observations are therefore severely hampered by
atmospheric seeing, and only the heftiest dark masses in the closest
galaxies can be detected. The situation in the last few years has improved
dramatically
with the advent of the Hubble Space Telescope (HST) and radio VLBI
techniques. The more subtle complication involves the actual modeling
of the stellar kinematics data, and in this area much progress has also
been made recently as well.
Here I will highlight some of the observational efforts during the past
two decades in searching for SMBHs, concentrating on the recent advances.
Since this contribution is the only one that discusses nuclear BHs
aside from that in the Milky Way (Ozernoy, these proceedings) and in
NGC 4258 (Miyoshi, these proceedings), I will attempt
to be as comprehensive as possible, although no claim to completeness is
made, as this is a vast subject and progress is being made at a dizzying
pace. To fill in the gaps, I refer the reader to several other recent
review papers, each of which has a slightly different emphasis (KR;
Rees 1998;
Richstone 1998;
Ford et al. 1998;
van der Marel 1999).
2. EARLY CLUES FROM PHOTOMETRY
The prospect of finding massive BHs in globular clusters motivated
much early effort to investigate the distribution of stars resulting
from the
adiabatic growth of a BH in a preexisting stellar system. The central
density deviates strongly from that of an isothermal core and instead
follows a cuspy profile
 (r)
(r)
 r-3/2
(Young 1980)
or steeper if two-body relaxation
(Peebles 1972;
Bahcall & Wolf 1976)
or different initial density profiles
(Quinlan, Hernquist, &
Sigurdsson 1995)
are taken into account. The discovery that the centers of
some giant elliptical galaxies obey this prediction
generated much enthusiasm for the existence of SMBHs. In the
well-known case of M87
(Young et al. 1978),
Lauer et al. (1992)
have since shown that the central cusp persists to the limit of the
resolution of the HST (0".1).
r-3/2
(Young 1980)
or steeper if two-body relaxation
(Peebles 1972;
Bahcall & Wolf 1976)
or different initial density profiles
(Quinlan, Hernquist, &
Sigurdsson 1995)
are taken into account. The discovery that the centers of
some giant elliptical galaxies obey this prediction
generated much enthusiasm for the existence of SMBHs. In the
well-known case of M87
(Young et al. 1978),
Lauer et al. (1992)
have since shown that the central cusp persists to the limit of the
resolution of the HST (0".1).
However, as emphasized by Kormendy
(1993;
see also KR), photometric signatures
alone do not uniquely predict the presence of a SMBH. The cores of most
galaxies are now known to be nonisothermal. And moreover, contrary to
naïve expectations, galaxy cores with high central surface
brightnesses and
small core radii, far from being the ones most likely to host SMBHs, are
in fact least expected to do so. This apparently contradictory
statement can be most easily understood by considering the so-called
fundamental-plane relations for the spheroidal component of galaxies
(Faber et al. 1987;
Bender, Burstein & Faber
1992).
More luminous, more
massive galaxies tend to have more massive central BHs
(Section 7), but
they also have larger, more diffuse cores.
Indeed, high-resolution photometric studies of early-type galaxies
(Nieto et al. 1991;
Crane et al. 1993;
Jaffe et al. 1994;
Lauer et al. 1995)
find that the central surface brightness profiles either continue
to rise toward the center as
I(r)  r-
r- , with
, with

 0.5-1.0 (the "power-law"
galaxies) or they flatten at some characteristic radius to a shallower
slope of
0.5-1.0 (the "power-law"
galaxies) or they flatten at some characteristic radius to a shallower
slope of 
 0.0-0.3
(the "core" galaxies). The power-law galaxies are invariably lower
luminosity, lower mass systems compared to those with distinct cores.
0.0-0.3
(the "core" galaxies). The power-law galaxies are invariably lower
luminosity, lower mass systems compared to those with distinct cores.
In summary, photometric signatures alone cannot be used as reliable
indicators for the presence of SMBHs. Instead, we must turn to the more
arduous task of obtaining kinematic measurements.
3. METHODS BASED ON STELLAR KINEMATICS
Contrary to the ambiguity of light profiles, the Keplerian rise in the
velocity dispersion toward the center,
 (r)
(r)
 r-1/2,
is a robust prediction for a wide variety of dynamical models containing a
central massive dark object (MDO;
Quinlan et al. 1995).
Sargent et al. (1978)
noticed that the innermost
velocities of M87 were consistent with such a prediction, and,
assuming an
isotropic velocity distribution, they inferred that the center of this
galaxy contained a dark mass of ~ 5 × 109
M
r-1/2,
is a robust prediction for a wide variety of dynamical models containing a
central massive dark object (MDO;
Quinlan et al. 1995).
Sargent et al. (1978)
noticed that the innermost
velocities of M87 were consistent with such a prediction, and,
assuming an
isotropic velocity distribution, they inferred that the center of this
galaxy contained a dark mass of ~ 5 × 109
M , presumably in
the form of a SMBH. The central rise in
, presumably in
the form of a SMBH. The central rise in
 (r), unfortunately,
can be insidiously
mimiced by an anisotropic velocity distribution, and therefore an MDO is
not required by the data for this object
(Duncan & Wheeler 1980;
Binney & Mamon 1982;
Richstone & Tremaine
1985;
Dressler & Richstone 1990;
van der Marel 1994a).
This degeneracy presents a serious difficulty for many mass
determinations based on stellar kinematic data. An extensive and lucid
discussion of this vast subject was presented by KR, and many of the
details will not be repeated here. Nonetheless, an abbreviated synopsis
is needed to motivate the topic.
(r), unfortunately,
can be insidiously
mimiced by an anisotropic velocity distribution, and therefore an MDO is
not required by the data for this object
(Duncan & Wheeler 1980;
Binney & Mamon 1982;
Richstone & Tremaine
1985;
Dressler & Richstone 1990;
van der Marel 1994a).
This degeneracy presents a serious difficulty for many mass
determinations based on stellar kinematic data. An extensive and lucid
discussion of this vast subject was presented by KR, and many of the
details will not be repeated here. Nonetheless, an abbreviated synopsis
is needed to motivate the topic.
Following the notation of KR, the radial variation in mass
can be expressed by the first velocity moment of the collisionless
Boltzman equation,
where V is the rotational velocity,
 r is the radial and
r is the radial and

 and
and

 the azimuthal components of
the velocity dispersion, and
the azimuthal components of
the velocity dispersion, and  is
the density of the tracer population.
In practice, several simplifying assumptions are adopted: (1) the mass
distribution is spherically symmetric; (2) the mean rotation is circular;
and (3)
is
the density of the tracer population.
In practice, several simplifying assumptions are adopted: (1) the mass
distribution is spherically symmetric; (2) the mean rotation is circular;
and (3)  is proportional to the
luminosity density, or,
equivalently, that M/L does not vary with radius.
is proportional to the
luminosity density, or,
equivalently, that M/L does not vary with radius.
A brief scrutiny of the above equation indicates that the effects of
velocity anisotropy can have a large and complicated effect on the
derivation of M(r)
because the terms inside the bracket significantly affect the
 r2
r / G term. If
r2
r / G term. If
 r >
r >

 and
and  r >
r >

 , each of the last two terms
will be negative
and can be as large as -1. The central brightness distributions of the
spheroidal component of most galaxies typically have
- (dln
, each of the last two terms
will be negative
and can be as large as -1. The central brightness distributions of the
spheroidal component of most galaxies typically have
- (dln  /
dln r)
/
dln r)  +
1.1 for luminous, nonrotating systems and
+
1.1 for luminous, nonrotating systems and
 +2 for low to
intermediate-luminosity systems (e.g.,
Faber et al. 1997).
Since - (dln
+2 for low to
intermediate-luminosity systems (e.g.,
Faber et al. 1997).
Since - (dln
 r2 /
dln r)
r2 /
dln r)  + 1,
it is apparent that, under suitable conditions, all four terms can largely
cancel one another. As emphasized by KR, all else being equal, smaller,
lower luminosity galaxies such as M32 potentially yield more secure mass
determinations than massive galaxies like M87 because less luminous systems
tend to have (1) steeper central light profiles, (2) a greater degree of
rotational support, and (3) less anisotropy.
+ 1,
it is apparent that, under suitable conditions, all four terms can largely
cancel one another. As emphasized by KR, all else being equal, smaller,
lower luminosity galaxies such as M32 potentially yield more secure mass
determinations than massive galaxies like M87 because less luminous systems
tend to have (1) steeper central light profiles, (2) a greater degree of
rotational support, and (3) less anisotropy.
The principles behind the stellar kinematics analysis are conceptually
straightforward but in practice technically challenging. Given the
set of observed quantities I(r), V(r), and
 (r), the goal is to
derive a range intrinsic values for these quantities after accounting for
projection and the blurring effects of seeing. Much of the machinery for
these tasks has been developed and extensively discussed by Kormendy
(1988a,
b) and
Dressler & Richstone
(1988).
The sensitivity of the
results to the effects of anisotropy are examined through maximum-entropy
dynamical models
(Richstone & Tremaine
1984,
1988)
to see whether conclusions regarding the presence of MDOs can be obviated
by a suitable exploration of parameter space. Perhaps the most serious
limitation of these maximum-entropy models is that they do not properly
take flattening into account.
(r), the goal is to
derive a range intrinsic values for these quantities after accounting for
projection and the blurring effects of seeing. Much of the machinery for
these tasks has been developed and extensively discussed by Kormendy
(1988a,
b) and
Dressler & Richstone
(1988).
The sensitivity of the
results to the effects of anisotropy are examined through maximum-entropy
dynamical models
(Richstone & Tremaine
1984,
1988)
to see whether conclusions regarding the presence of MDOs can be obviated
by a suitable exploration of parameter space. Perhaps the most serious
limitation of these maximum-entropy models is that they do not properly
take flattening into account.
The last several years have seen a resurged interest in improving the
techniques of analyzing stellar kinematics data. In the context of SMBH
searches,
Gerhard (1993),
van der Marel et al.
(1994a,
b),
Dehnen (1995),
among others, have stressed the importance of utilizing the full
information contained in the velocity profile or line-of-sight velocity
distribution (LOSVD) of the absorption lines, which
are normally treated only as Gaussians. A system with significant
rotation, for instance, can leave a measurable skewness on the LOSVD, while
various degrees of anisotropy would imprint symmetric deviations from a
Gaussian line shape. Neglecting these subtleties can lead to systematic
errors in the measurement of V(r), but in the cases best
studied so far
these effects do not seem to have been severe (KR). Furthermore, the
line profile should develop weak, high-velocity wings if a SMBH is present
(van der Marel 1994b),
although the currently available data do not yet have
the requisite quality to exploit this tool.
Yet another advance has focused on the development of dynamical models with
two-integral phase-space distribution functions, f (E,
Lz), E being the
total energy and Lz the angular momentum in the
symmetry axis
(van der Marel et al. 1994b;
Qian et al. 1995;
Dehnen 1995).
Such models are properly
flattened, and they generate predictions for the LOSVDs; on the
other hand, it is not clear whether imposing a special dynamical structure
is too restrictive. This limitation will be eliminated by fully general,
axisymmetric three-integral models
(van der Marel et al. 1998;
Cretton et al. 1999;
Gebhardt et al. 1998).
There are currently 10 galaxies with published MDO measurements determined
from stellar kinematical data (Table 1).
Of these, only three (M81:
Bower et al. 1996;
NGC 3379:
Gebhardt et al. 1998;
NGC 4342:
van den Bosch 1998)
come solely from HST data; the remaining ones, although
many by now confirmed with HST, were initially discovered
from high-quality ground-based observations (see KR for a detailed account
of each object). Kormendy and collaborators, in particular, making use of
the excellent seeing conditions and instrumentation on the CFHT,
continue to make progress in this area. Two new MDOs have been reported
recently based
on CFHT data: the low-luminosity elliptical galaxy NGC 4486B has
MMDO = 6 × 108
M (Kormendy et al. 1997b),
and NGC 3377, another close cousin, has
MMDO = 2.3 × 108
M
(Kormendy et al. 1997b),
and NGC 3377, another close cousin, has
MMDO = 2.3 × 108
M (Kormendy et al. 1998).
This demonstrates the important fact that
even in the HST era ground-based observations continue to play an
important role in SMBH searches.
(Kormendy et al. 1998).
This demonstrates the important fact that
even in the HST era ground-based observations continue to play an
important role in SMBH searches.
The new observations with HST, thus far all acquired using the
Faint Object Spectrograph (FOS), provide an important contribution by
increasing the angular resolution by about a factor of 5 compared to the
best ground-based data available. In all cases studied (NGC 3115:
Kormendy et al. 1996;
NGC 4594:
Kormendy et al. 1997a;
M32:
van der Marel et al. 1997;
M31:
Ford et al. 1998),
the velocity dispersions continue to rise toward
smaller r and the maximum rotational velocity has generally
increased (Fig. 1). In the case of NGC 3115,
the FOS spectra are of sufficient
quality to reveal wings in the LOSVD that extend up to ~ 1200 km
s-1
(Kormendy et al. 1996).
The HST data thus considerably bolster the case
for a MDO in these objects. The improvement in angular resolution
additionally strengthens our confidence that the MDOs might indeed be
SMBHs. A reduction of the size scale by a factor of 5 increases the
central density by more than
two orders of magnitude. Although in general this is still not enough to
rule out alternative explanations for the dark mass
(Section 6), it is
clearly a step in the right direction.

|
Figure 1. Stellar kinematic data for
NGC 3115 compared with various dynamical models (see
Kormendy et al. 1996).
The left panel shows
the best ground-based data, and the right panel the same data with
new HST data superposed for comparison. Both V and
 rise
much more steeply with radius in the new HST data. rise
much more steeply with radius in the new HST data.
|
I conclude this section with a few remarks on the dark mass in
the Galactic Center (see Ozernoy in these proceedings for more details),
which, in my view, is now the most compelling case of a SMBH in any
galactic nucleus. From analysis of an extensive set of near-IR radial
velocities of individual stars, coupled with
additional measurements from the literature, Genzel et al.
(1996;
see also
Krabbe et al. 1995)
found a highly statistically significant rise in the radial
velocity dispersion between 5 and 0.1 pc from the dynamical center.
Assuming
an isotropic velocity distribution, the observations require a dark mass
of ~ 3 × 106
M within r =
0.1 pc and
M/LK
within r =
0.1 pc and
M/LK  100;
the dark mass must have a density in excess of 109
M
100;
the dark mass must have a density in excess of 109
M pc-3, which argues strongly for it being a SMBH. These
conclusions, and a suspicion nearly three decades old
(Lynden-Bell & Rees 1971),
have finally been vindicated by recent measurements of stellar proper
motions within the central 1 pc region using high-resolution
K-band astrometric maps
(Eckart & Genzel 1996,
1997;
Genzel et al. 1997;
Ghez et al. 1998).
The main results are the following: (1) the stellar radial velocities
agree
with the proper motions, which implies that on average the velocities are
close to isotropic; (2) the combined velocities imply a dark mass
(Fig. 2)
within 0.006 pc of 2.61 × 106
M
pc-3, which argues strongly for it being a SMBH. These
conclusions, and a suspicion nearly three decades old
(Lynden-Bell & Rees 1971),
have finally been vindicated by recent measurements of stellar proper
motions within the central 1 pc region using high-resolution
K-band astrometric maps
(Eckart & Genzel 1996,
1997;
Genzel et al. 1997;
Ghez et al. 1998).
The main results are the following: (1) the stellar radial velocities
agree
with the proper motions, which implies that on average the velocities are
close to isotropic; (2) the combined velocities imply a dark mass
(Fig. 2)
within 0.006 pc of 2.61 × 106
M (Genzel et al. 1997
quote a statistical error of ± 0.15 and a combined statistical and
systematic error of
± 0.35); (3) the density, therefore, has an astonishingly high
value of >2 × 1012
M
(Genzel et al. 1997
quote a statistical error of ± 0.15 and a combined statistical and
systematic error of
± 0.35); (3) the density, therefore, has an astonishingly high
value of >2 × 1012
M pc-3,
which leaves almost no room to escape the
conclusion that the dark mass must be in the form of a SMBH
(Section 6). The
presence of a large mass is also supported by the detection of several
stars, within 0.01 pc from the central radio source Sgr A*, moving
at speeds in
excess of 1000 km s-1. From the velocities of the
fast-moving stars and the near
stationarity of Sgr A*, Genzel et al. further use equipartition
arguments to constrain the mass of the radio core itself
(
pc-3,
which leaves almost no room to escape the
conclusion that the dark mass must be in the form of a SMBH
(Section 6). The
presence of a large mass is also supported by the detection of several
stars, within 0.01 pc from the central radio source Sgr A*, moving
at speeds in
excess of 1000 km s-1. From the velocities of the
fast-moving stars and the near
stationarity of Sgr A*, Genzel et al. further use equipartition
arguments to constrain the mass of the radio core itself
( 105
M
105
M ), which, when
combined with the exceedingly small upper limit
for its size (r < 4 × 10-6 pc), would imply a
density of > 3 × 1020
M
), which, when
combined with the exceedingly small upper limit
for its size (r < 4 × 10-6 pc), would imply a
density of > 3 × 1020
M pc-3.
pc-3.
4. METHODS BASED ON GAS KINEMATICS
Unlike the situation for stars, gas kinematics are much easier to interpret
if the gas participates in Keplerian rotation in a disklike
configuration. But
there are two caveats to remember. First, gas can be easily perturbed by
nongravitational forces (shocks, radiation pressure, winds, magnetic
fields, etc.). Indeed, in the case of the Galactic Center, it was
precisely this
reason that its central mass, which had been estimated for some time using
gas velocities
(Lacy et al. 1980),
could not be accepted with full confidence
prior to the measurement of the stellar kinematics. Second, there is
no a priori reason that the gas should be in dynamical equilibrium,
and therefore one must verify empirically that the velocity field indeed
is Keplerian. The optically-emitting ionized gas in the central regions of
some spirals show significant noncircular motions (e.g.,
Fillmore, Boroson, &
Dressler 1986).
NGC 4594 is a striking example.
Kormendy et al. (1997a)
showed that the emission-line rotation curve near the center falls
substantially below the circular velocities of the stars, and
hence the gas kinematics cannot be used to determine the central mass.
4.1. Optical Emission Lines
The sharpened resolution of the refurbished HST has revealed many
examples of nuclear disks of dust and ionized gas
(Fig. 3). The nuclear disks
typically have diameters ~ 100-300 pc, with the minor axis often
aligned along the direction of the radio jet, if present. Some examples
include the elliptical galaxies NGC 4261
(Jaffe et al. 1993),
M87
(Ford et al. 1994),
NGC 5322
(Carollo et al. 1997),
and NGC 315
(Ho et al. 1997),
and the early-type spiral M81
(Devereux, Ford, & Jacoby
1997).
I will highlight here only three cases; Table 1
gives a complete list of objects and references.

|
Figure 3. Nuclear disks from HST
optical images. Each image is 35" on a side.
|
The first object for which the nuclear gas disk was used to determine the
central mass was M87.
Harms et al. (1994)
used the FOS to obtain spectra of several positions of the disk and
measured a velocity difference of ± 1000 & km& s-1 at a
radius of 0".25 (18
pc) on either side of the nucleus. Adopting an inclination angle of
42° determined photometrically by
Ford et al. (1994),
the velocities were consistent with Keplerian motions about a central
mass of (2.4± 0.7) × 109
M . Since the implied
M / LV
. Since the implied
M / LV
 500, Harms et
al. concluded that the central mass is
dark, most likely in the form of a SMBH. The case for a SMBH in M87 has
been considerably strengthened through the recent reobservation with
HST by
Macchetto et al. (1997),
who used the long-slit mode of the
Faint Object Camera to obtain higher quality spectra extending to
r = 0".05 (3.5 pc). The velocities in the inner few tenths
of an arcsecond
are well fitted by a model of a thin disk in Keplerian rotation
(Fig. 4),
although the inclination angle is not well constrained (47°-65°).
The rotation curve at larger radii falls below the Keplerian curve,
possibly indicating a warp in the disk
(Macchetto et al. 1997)
or substantial perturbations due to spiral shocks
(Chakrabarti 1995).
For i = 52°, MMDO = (3.2± 0.9) ×
109
M
500, Harms et
al. concluded that the central mass is
dark, most likely in the form of a SMBH. The case for a SMBH in M87 has
been considerably strengthened through the recent reobservation with
HST by
Macchetto et al. (1997),
who used the long-slit mode of the
Faint Object Camera to obtain higher quality spectra extending to
r = 0".05 (3.5 pc). The velocities in the inner few tenths
of an arcsecond
are well fitted by a model of a thin disk in Keplerian rotation
(Fig. 4),
although the inclination angle is not well constrained (47°-65°).
The rotation curve at larger radii falls below the Keplerian curve,
possibly indicating a warp in the disk
(Macchetto et al. 1997)
or substantial perturbations due to spiral shocks
(Chakrabarti 1995).
For i = 52°, MMDO = (3.2± 0.9) ×
109
M , and M /
LV
, and M /
LV
 110.
If, instead, a Plummer potential is assumed, the distributed dark mass can
have a core radius no larger than ~ 5 pc. So, in either case, a density
~ 107 M
110.
If, instead, a Plummer potential is assumed, the distributed dark mass can
have a core radius no larger than ~ 5 pc. So, in either case, a density
~ 107 M pc-3 is implied.
pc-3 is implied.
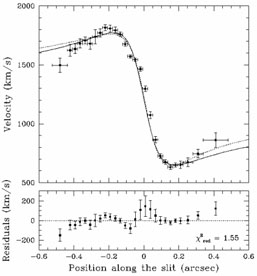
|
Figure 4. Optical emission-line rotation
curve for the nuclear disk in M87.
The two curves in the upper panel correspond to Keplerian thin disk
models, and the bottom panel shows the residuals for one of the models
(see
Macchetto et al. 1997).
|
The mildly active nucleus of NGC 4261 contains a rotating disk of dust and
ionized gas as well
(Ferrarese, Ford, & Jaffe
1996);
like M87, the disk
is slightly warped and shows traces of weak spiral structure.
Although the FOS data for this object are rather noisy, they indicate
that the gas largely undergoes circular motions. The mass interior
to r = 15 pc is
MMDO = (4.9± 1.0) × 108
M , and
M/LV has an exceptionally high value of 2
× 103.
, and
M/LV has an exceptionally high value of 2
× 103.
The installation of the imaging spectrograph STIS in 1997
at long last gives HST an efficient means to obtain spatially
resolved spectra of the central regions of galaxies. Much progress in the
field is anticipated in the near future. A taste of what might
be expected can be seen in the early-release observations of M84
by Bower et al.
(1998;
Fig. 5). M84 is almost a twin of M87 in terms of
luminosity, and its central dark mass (1.5 × 109
M ), too, is similar.
), too, is similar.
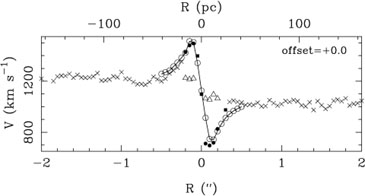
|
Figure 5. Optical emission-line rotation
curve for the nuclear disk in M84 obtained with STIS on HST
(Bower et al. 1998).
The kinematics can be
well fitted with a thin Keplerian disk model, which is plotted as
open circles connected by the solid line.
|
Lastly, I mention an interesting, unconventional case. The radio galaxy
Arp 102B belongs to a minority of AGNs that display
so-called double-peaked
broad emission lines. Several ideas have been proposed for the peculiar
line profiles in this class of objects, but the favored explanation is that
the lines originate from a relativistic accretion disk
(Eracleous et al. 1997).
During the course of a long-term optical monitoring
of Arp 102B, the intensity ratio of the two peaks of the
H line
displayed sinusoidal variations with a period of 2.2 years for several
years
(Newman et al. 1997).
The periodic signal was interpreted as
arising from a "hot spot" in the accretion disk. By modeling the
line profile from the epochs when the hot spot was quiescent, one can
estimate the radius and inclination angle of the spot's orbit, and,
combined with its period, the enclosed mass. The mass within r =
0.005 pc turns out to be 2.2 × 108
M
line
displayed sinusoidal variations with a period of 2.2 years for several
years
(Newman et al. 1997).
The periodic signal was interpreted as
arising from a "hot spot" in the accretion disk. By modeling the
line profile from the epochs when the hot spot was quiescent, one can
estimate the radius and inclination angle of the spot's orbit, and,
combined with its period, the enclosed mass. The mass within r =
0.005 pc turns out to be 2.2 × 108
M , consistent with
a moderately luminous
(MB&
, consistent with
a moderately luminous
(MB&  -20 mag) elliptical (see Section 7).
-20 mag) elliptical (see Section 7).
4.2. Radio Spectroscopy of Water Masers
Luminous 22-GHz emission from extragalactic water masers are preferentially
detected in galaxies with active nuclei, where physical conditions,
possibly realized in a circumnuclear disk
(Claussen & Lo 1986),
evidently favor this form of maser emission. With the detection in
NGC 4258 of
high-velocity features offset from the systemic velocity by ~ ± 900
& km& s-1
(Nakai, Inoue, & Miyoshi
1993),
Watson & Wallin (1994)
already surmised
that the maser spectrum of this Seyfert galaxy can be interpreted as
arising from a thin Keplerian disk rapidly rotating around a mass of ~
107
M . But the solid
proof of this picture came from the high-resolution
(
. But the solid
proof of this picture came from the high-resolution
(
 = 0".0006 ×
0".0003;
= 0".0006 ×
0".0003;  v = 0.2
& km& s-1) VLBA observations of
Miyoshi et al. (1995)
who demonstrated that the maser spots
trace a thin (< 0.003 pc), nearly edge-on annulus with an inner radius
of 0.13 pc and an outer radius of 0.26 pc. The systemic features lie
on the near side of the disk along the line-of-sight to the center
(Fig. 6);
the high-velocity features delineate the edges of the disk on either
side and follow a Keplerian rotation curve to very high accuracy
(
v = 0.2
& km& s-1) VLBA observations of
Miyoshi et al. (1995)
who demonstrated that the maser spots
trace a thin (< 0.003 pc), nearly edge-on annulus with an inner radius
of 0.13 pc and an outer radius of 0.26 pc. The systemic features lie
on the near side of the disk along the line-of-sight to the center
(Fig. 6);
the high-velocity features delineate the edges of the disk on either
side and follow a Keplerian rotation curve to very high accuracy
( 1%). The
implied binding mass within 0.13 pc is 3.6 × 107
M
1%). The
implied binding mass within 0.13 pc is 3.6 × 107
M , which
corresponds to a density of > 4 × 109
M
, which
corresponds to a density of > 4 × 109
M pc-3. In fact, one can
place a tighter constraint on the density. The maximum deviation of the
velocities from a Keplerian rotation curve limits the extent of the central
mass to r
pc-3. In fact, one can
place a tighter constraint on the density. The maximum deviation of the
velocities from a Keplerian rotation curve limits the extent of the central
mass to r
 0.012 pc
(Maoz 1995),
from which follows that the density must be > 5 × 1012
M
0.012 pc
(Maoz 1995),
from which follows that the density must be > 5 × 1012
M pc-3.
pc-3.
Two, possibly three, additional AGNs have H2O megamasers
suitable for tracing the central potential. The spectrum of the maser
source in the Seyfert nucleus of NGC 1068 also exhibits satellite
features (± 300 & km& s-1) offset from the systemic velocity
(Greenhill et al. 1996).
The redshifted and
blueshifted emission again lie on a roughly linear, 2-parsec feature
passing through the systemic emission
(Greenhill 1998).
The rotation curve in this
instance is sub-Keplerian, possibly because the disk has nonnegligible mass,
and the derived mass (1.7 × 107
M within a radius
of 0.65 pc) is less certain.
within a radius
of 0.65 pc) is less certain.
The maser in the nucleus of NGC 4945 shows a position and
velocity distribution reminiscent of NGC 4258 as well: high-velocity
features symmetrically straddle the systemic emission.
Greenhill, Moran, &
Herrnstein (1997)
interpret the data, which in this case is
considerably less accurate because of its location in the southern sky,
in terms of an edge-on disk model and derive a central mass of 1.4
× 106
M within r =
0.3 pc. This result is quite surprising because,
as an Scd spiral, NGC 4945 is expected to be essentially bulgeless. If
the dark mass in its center is truly in the form of a SMBH, then SMBHs
evidently can form without a bulge.
within r =
0.3 pc. This result is quite surprising because,
as an Scd spiral, NGC 4945 is expected to be essentially bulgeless. If
the dark mass in its center is truly in the form of a SMBH, then SMBHs
evidently can form without a bulge.
The H2O megamaser source in NGC 3079 is potentially useful
for mass determination. Here, however, the complex spatial distribution
of the emission regions and the large intrinsic widths of the lines
complicate the analysis, and the interpretation of the data may not be
unique.
Trotter et al. (1998)
tentatively assign a central mass of 1 × 106
M to this galaxy.
to this galaxy.
4.3. Determining Central Masses of Active Galactic
Nuclei
I mention one other method for determining masses in the central regions of
galaxies, specifically in AGNs. Although AGNs largely provide the motivation
for searching for SMBHs, ironically it is precisely in these objects that
conventional techniques used to measure masses fail. The bright continuum
emission of the active nucleus nearly always completely overpowers the
stellar absorption lines near the center, and in many cases the narrow
emission lines are significantly affected by nongravitational forces.
An approach taken in the past attempts to utilize the
broad [(1-few) × 103 & km& s-1] emission
lines that are thought to arise
from the so-called broad-line region (BLR), a tiny, dense region
much less than a parsec from the central source. Assuming that the line
widths trace gravity, the mass follows from
 v2rBLR / G, where
v2rBLR / G, where

 1-3 depending on the
kinematic model adopted. The BLR radius has traditionally been estimated
from photoionization arguments (e.g.,
Dibai 1980;
Wandel & Yahil 1985;
Wandel & Mushotzky 1986;
Padovani, Burg, & Edelson
1990),
but recent variability studies indicate that the BLR is much more
compact than previously thought
(Netzer & Peterson 1997).
1-3 depending on the
kinematic model adopted. The BLR radius has traditionally been estimated
from photoionization arguments (e.g.,
Dibai 1980;
Wandel & Yahil 1985;
Wandel & Mushotzky 1986;
Padovani, Burg, & Edelson
1990),
but recent variability studies indicate that the BLR is much more
compact than previously thought
(Netzer & Peterson 1997).
The continuum output from AGNs typically varies on
timescales ranging from days to months in the UV and optical bands.
Because the emission lines are predominantly photoionized by the central
continuum, they vary in response to the changes in the continuum, but with
a time delay (lag) that corresponds to the light-travel distance between the
continuum source and the line-emitting gas.
"Reverberation mapping"
(Blandford & McKee 1982),
therefore, in
principle allows one to estimate the luminosity-weighted radius of the BLR,
although in practice the complex geometry and ionization structure of
the BLR complicate the interpretation of the "sizes" derived by this method
(see
Netzer & Peterson 1997
for a recent review).
If the widths of the broad emission lines reflect bound gravitational
motions, as seems to be the case in most well-studied objects
(Netzer & Peterson 1997;
but see
Krolik 1997),
then, adopting a reasonable kinematic model
(e.g., randomly moving clouds), the virial mass can be
estimated from v2rBLR /
G. If, instead, the clouds are
infalling, as has been claimed in some cases, the mass will be smaller by a
factor of 2. One of the uncertainties in the application of this simple
formalism lies in the choice of v. What is appropriate? One
reasonable choice might be v =
( 3 / 2)FWHM, the full width at
half-maximum of a
representative broad line. Yet another ambiguity is which line to use,
since not all broad emission lines have the same widths. Ultraviolet or
high-ionization lines, for instance, generally have broader profiles than
optical or low-ionization lines. For the purposes of this exercise, I
simply chose the line for which the most data exist
(H
3 / 2)FWHM, the full width at
half-maximum of a
representative broad line. Yet another ambiguity is which line to use,
since not all broad emission lines have the same widths. Ultraviolet or
high-ionization lines, for instance, generally have broader profiles than
optical or low-ionization lines. For the purposes of this exercise, I
simply chose the line for which the most data exist
(H ) in order to obtain
as large a sample as possible.
) in order to obtain
as large a sample as possible.
Table 2 lists the derived masses for the 17
Seyfert 1 galaxies that have been
monitored extensively in the optical; eight of the objects appear in the
compilation of
Peterson et al. (1998).
Since the masses of MDOs
derived from gas and stellar kinematics show a loose correlation with the
bulge or spheroidal luminosity of the host galaxies
(Section 7;
Fig. 8 a),
we can ask whether those derived from reverberation mapping follow such a
correlation. I have estimated the B-band luminosities of the
bulges of the Seyferts based on published surface photometry of the host
galaxies (taking care to exclude the contribution of the AGN itself,
which often can be
significant). Figure 8 b
indicates that, at a fixed bulge luminosity,
the masses from reverberation mapping are systematically lower
than the
masses obtained using conventional techniques, on average by about a factor
of 5. It is encouraging that this admittedly crude method of mass
estimation is not too far off the mark. Notably, the scatter of
MMDO at a fixed luminosity is quite comparable in the
two samples,
and the constant offset suggests that one of the underlying assumptions
in the mass estimate is incorrect. Since the line width affects the mass
quadratically, it is conceivable that some measure of the line profile other
than the FWHM is more appropriate.
5. INDIRECT, BUT TANTALIZING EVIDENCE
Lastly, one additional piece of evidence, although it does not give a
direct measure of the central mass, cannot go unmentioned - namely the
recent detection in AGNs of the broad iron
K line at 6.4 keV.
This line has been known for some time to be a common feature in the hard
X-ray spectra of AGNs, and it is thought to arise from fluorescence of
the X-ray continuum off of cold material, presumably associated with the
accretion disk around the SMBH (e.g.,
Pounds et al. 1990).
The spectral
resolution of the existing data, however, was insufficient to
test the predicted line profile
(Fabian et al. 1989).
The ASCA
satellite provided the much-awaited tell-tale signs in the deep exposure
of the Seyfert 1 galaxy MCG-6-30-15
(Tanaka et al. 1995):
the Fe K
line at 6.4 keV.
This line has been known for some time to be a common feature in the hard
X-ray spectra of AGNs, and it is thought to arise from fluorescence of
the X-ray continuum off of cold material, presumably associated with the
accretion disk around the SMBH (e.g.,
Pounds et al. 1990).
The spectral
resolution of the existing data, however, was insufficient to
test the predicted line profile
(Fabian et al. 1989).
The ASCA
satellite provided the much-awaited tell-tale signs in the deep exposure
of the Seyfert 1 galaxy MCG-6-30-15
(Tanaka et al. 1995):
the Fe K line
exhibits Doppler motions that approach relativistic speeds (~ 100,000
km s-1 or 0.3c!) as well as an asymmetric red wing
consistent with
gravitational redshift. The best-fitting disk has an inner radius of
6 Schwarzschild radii. The relativistic Fe
K
line
exhibits Doppler motions that approach relativistic speeds (~ 100,000
km s-1 or 0.3c!) as well as an asymmetric red wing
consistent with
gravitational redshift. The best-fitting disk has an inner radius of
6 Schwarzschild radii. The relativistic Fe
K line, now seen
in a large number of sources
(Nandra et al. 1997;
Fig. 7), provides arguably
the most compelling evidence to date for the existence of SMBHs. Other
mechanisms for generating the line profile are possible, but implausible
(Fabian et al. 1995).
Detailed modeling of the line asymmetry has even the
potential to measure the spin of the hole, but this is still very
much a goal of the future given the current data quality and
uncertainties in the modeling itself (e.g.,
Reynolds & Begelman 1997;
Rybicki & Bromley 1998).
line, now seen
in a large number of sources
(Nandra et al. 1997;
Fig. 7), provides arguably
the most compelling evidence to date for the existence of SMBHs. Other
mechanisms for generating the line profile are possible, but implausible
(Fabian et al. 1995).
Detailed modeling of the line asymmetry has even the
potential to measure the spin of the hole, but this is still very
much a goal of the future given the current data quality and
uncertainties in the modeling itself (e.g.,
Reynolds & Begelman 1997;
Rybicki & Bromley 1998).

|
Figure 7.The Fe
K line in the
composite spectrum of Seyfert 1 nuclei
(Nandra et al. 1997).
The solid line is a fit to the line profile
using two Gaussians, a narrow component centered at 6.4 keV and a much
broader, redshifted component. line in the
composite spectrum of Seyfert 1 nuclei
(Nandra et al. 1997).
The solid line is a fit to the line profile
using two Gaussians, a narrow component centered at 6.4 keV and a much
broader, redshifted component.
|
6. ARE THE MASSIVE DARK OBJECTS REALLY BLACK HOLES?
Thus far we have rigorously shown only that many galaxies contain
central MDOs,
not that the dark masses must be in the form of SMBHs. Direct proof of
the existence of SMBHs would require the detection of relativistic motions
emanating from the vicinity of the Schwarzschild radius,
RS =
2GM /
c2
/
c2  10-5(M
10-5(M / 108
M
/ 108
M ) pc.
Even for our neighbor M31, RS subtends 3 ×
10-6 arcseconds, and the
Galactic Center only a factor of 2 larger. We are clearly still far from
being able to achieve the requisite angular resolution and in the meantime
must rely on indirect arguments.
) pc.
Even for our neighbor M31, RS subtends 3 ×
10-6 arcseconds, and the
Galactic Center only a factor of 2 larger. We are clearly still far from
being able to achieve the requisite angular resolution and in the meantime
must rely on indirect arguments.
One approach seeks to identify some observational feature that might be
taken as a fingerprint of the event horizon or of physical processes
uniquely associated with the environment of a BH. One such
"signature" might be the broad Fe
K line discussed in
Section 5; another
is the high-energy power-law tail observed in some AGNs and Galactic BH
candidates
(Titarchuk & Zannias
1998).
And yet a third possibility is the advection of matter into the event
horizon
(Menou, Quataert, & Narayan
1999).
line discussed in
Section 5; another
is the high-energy power-law tail observed in some AGNs and Galactic BH
candidates
(Titarchuk & Zannias
1998).
And yet a third possibility is the advection of matter into the event
horizon
(Menou, Quataert, & Narayan
1999).
A different strategy appeals to the dynamical stability of the probable
alternative sources of the dark mass
(Goodman & Lee 1989;
Richstone, Bower, &
Dressler 1990;
van der Marel et al. 1997;
Maoz 1998).
The absence of strong
radial gradients in the stellar population, as measured by variations in
color or spectral indices, implies that the large increase in M /
L toward the
center cannot be attributed to a cluster of ordinary stars. On the other
hand, the underluminous mass could, in principle, be a cluster of stellar
remnants (white dwarfs, neutron stars, and stellar-size BHs) or perhaps
even substellar objects (planets and brown dwarfs). To rule out these
possibilities, however exotic they might seem, one must show that the
clusters cannot have survived over the age of the galaxy, and hence
finding them would be highly improbable.
As most recently discussed by
Maoz (1998),
the two main processes that
determine the lifetime of a star cluster are evaporation, whereby stars
escape the cluster as a result of multiple weak gravitational scatterings,
and physical collisions among the stars themselves. Exactly which dominates
depends on the composition and size of the cluster, and its maximum
possible lifetime can be computed for any given mass and density.
Maoz (1998)
shows that in two galaxies, namely the Milky Way and NGC 4258, the
density of the dark mass is so high
( 1012
M
1012
M pc-3)
that it cannot
possibly be in the form of a stable cluster of stellar or substellar
remnants: their maximum ages [~ (1-few) × 108 yr] are
much less than the
ages of the galaxies. The only remaining constituents allowed appear to be
subsolar-mass BHs and elementary particles. This constitutes very
strong evidence that the MDOs - at least in two cases - are most likely
SMBHs. In the following discussion, I will adopt the simplifying
viewpoint that all MDOs are SMBHs, bearing in mind that at the current
resolution limit we cannot yet disprove the dark-cluster hypothesis for the
majority of the objects.
pc-3)
that it cannot
possibly be in the form of a stable cluster of stellar or substellar
remnants: their maximum ages [~ (1-few) × 108 yr] are
much less than the
ages of the galaxies. The only remaining constituents allowed appear to be
subsolar-mass BHs and elementary particles. This constitutes very
strong evidence that the MDOs - at least in two cases - are most likely
SMBHs. In the following discussion, I will adopt the simplifying
viewpoint that all MDOs are SMBHs, bearing in mind that at the current
resolution limit we cannot yet disprove the dark-cluster hypothesis for the
majority of the objects.
7. THE BLACK-HOLE MASS/BULGE MASS RELATION
Does
M depend
at all on other properties of the host galaxies? A
much-discussed possibility is that
M
depend
at all on other properties of the host galaxies? A
much-discussed possibility is that
M scales
with the mass of the spheroidal component of the host
(Kormendy 1993;
KR;
Faber et al. 1997;
Magorrian et al. 1998;
Richstone 1998;
Ford et al. 1998;
van der Marel 1999).
The significance of the scatter in the correlation, or whether any
correlation exists at all, is not yet certain. It is somewhat
disconcerting that different authors plotting the same objects do not
always arrive at the
same conclusion. The discrepancies can often be traced to different
assumptions about distances, source of bulge-to-disk decomposition, and
even apparent magnitudes adopted for the host galaxies (e.g., extinction is
not always corrected). The set of host galaxy parameters I adopt is
compiled in Table 1.
scales
with the mass of the spheroidal component of the host
(Kormendy 1993;
KR;
Faber et al. 1997;
Magorrian et al. 1998;
Richstone 1998;
Ford et al. 1998;
van der Marel 1999).
The significance of the scatter in the correlation, or whether any
correlation exists at all, is not yet certain. It is somewhat
disconcerting that different authors plotting the same objects do not
always arrive at the
same conclusion. The discrepancies can often be traced to different
assumptions about distances, source of bulge-to-disk decomposition, and
even apparent magnitudes adopted for the host galaxies (e.g., extinction is
not always corrected). The set of host galaxy parameters I adopt is
compiled in Table 1.
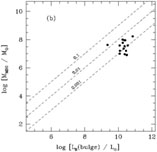
Figure 8 a illustrates that there indeed
appears to be a trend of
M increasing with bulge mass (luminosity). It is encouraging to
note that the central masses derived from gas and stellar kinematics do not
show any obvious systematic offsets relative to one another.
No obvious differentiation by Hubble type is evident either. As has been
noted by others, the scatter of
M
increasing with bulge mass (luminosity). It is encouraging to
note that the central masses derived from gas and stellar kinematics do not
show any obvious systematic offsets relative to one another.
No obvious differentiation by Hubble type is evident either. As has been
noted by others, the scatter of
M at a
given luminosity is
considerable, at least a factor of 10, perhaps up to 100. The scatter
may have been exacerbated slightly by four possibly anomalous points.
NGC 4486B is a companion to M87, and it appears to have been tidally
truncated; its original luminosity was probably higher. On the other hand,
the bulge luminosity of NGC 4945 could very well have been
overestimated. Its bulge-to-disk ratio was found using the relation of
Simien & de Vaucouleurs
(1986),
which may be inappropriate for a galaxy of such late Hubble type
(Scd). Finally, the masses of M81 and NGC 3079 are quite uncertain and
probably have been underestimated.
at a
given luminosity is
considerable, at least a factor of 10, perhaps up to 100. The scatter
may have been exacerbated slightly by four possibly anomalous points.
NGC 4486B is a companion to M87, and it appears to have been tidally
truncated; its original luminosity was probably higher. On the other hand,
the bulge luminosity of NGC 4945 could very well have been
overestimated. Its bulge-to-disk ratio was found using the relation of
Simien & de Vaucouleurs
(1986),
which may be inappropriate for a galaxy of such late Hubble type
(Scd). Finally, the masses of M81 and NGC 3079 are quite uncertain and
probably have been underestimated.
The trend is much more significant when five upper limits are included.
NGC 205, a dwarf elliptical companion of M31,
contains a blue, compact
nucleus with characteristics resembling an intermediate-age globular
cluster. Its core radius, determined from HST photometry,
combined with a
ground-based measurement of its velocity dispersion yields an upper
limit of 9 × 104
M for any dark mass
(Jones et al. 1996).
The bulgeless, late-type (Scd) spiral M33 also has a stringent upper
limit on its central mass. Its nuclear cluster is extremely tiny (core
radius
for any dark mass
(Jones et al. 1996).
The bulgeless, late-type (Scd) spiral M33 also has a stringent upper
limit on its central mass. Its nuclear cluster is extremely tiny (core
radius
 0.39 pc), and
its central velocity dispersion is 21 km s-1;
Kormendy & McClure (1993)
put an upper limit of
M
0.39 pc), and
its central velocity dispersion is 21 km s-1;
Kormendy & McClure (1993)
put an upper limit of
M
 5 × 104
M
5 × 104
M . NGC 4395 in
some ways resembles M33, but it is even more extreme. The nucleus is
optically classified as a type 1.8 Seyfert (broad
H
. NGC 4395 in
some ways resembles M33, but it is even more extreme. The nucleus is
optically classified as a type 1.8 Seyfert (broad
H and
H
and
H present),
emits a largely nonstellar featureless continuum that extends into the UV
(Filippenko, Ho, & Sargent
1993),
and displays variable
soft X-ray emission and a compact flat-spectrum radio core
(Moran et al. 1999).
These properties alone would be unremarkable were it not for the
fact that the nucleus has an absolute blue magnitude of only -9.8 and lives
in a Magellanic spiral 2.6 Mpc away!
Filippenko & Ho (1998)
detected the
Ca II infrared triplet lines in absorption from echelle spectra taken
with the Keck telescope, from which they were able to estimate the
strength of the stellar component contributing to the nuclear light
(MB = -7.3 mag) and the central stellar velocity
dispersion (
present),
emits a largely nonstellar featureless continuum that extends into the UV
(Filippenko, Ho, & Sargent
1993),
and displays variable
soft X-ray emission and a compact flat-spectrum radio core
(Moran et al. 1999).
These properties alone would be unremarkable were it not for the
fact that the nucleus has an absolute blue magnitude of only -9.8 and lives
in a Magellanic spiral 2.6 Mpc away!
Filippenko & Ho (1998)
detected the
Ca II infrared triplet lines in absorption from echelle spectra taken
with the Keck telescope, from which they were able to estimate the
strength of the stellar component contributing to the nuclear light
(MB = -7.3 mag) and the central stellar velocity
dispersion (
 30 km s-1).
Combining the velocity dispersion with a cluster size (r
30 km s-1).
Combining the velocity dispersion with a cluster size (r
 0.7 pc)
obtained from HST images, Filippenko & Ho limit the central
mass to
0.7 pc)
obtained from HST images, Filippenko & Ho limit the central
mass to  8 ×
104
M
8 ×
104
M . The Circinus
galaxy is thought to house a Seyfert
nucleus, and if it contains a SMBH, its mass within
r
. The Circinus
galaxy is thought to house a Seyfert
nucleus, and if it contains a SMBH, its mass within
r  10 pc has
been constrained to be
10 pc has
been constrained to be
 4 ×
106
M
4 ×
106
M (Maiolino et al. 1998).
The last upper limit shown in the figure pertains to the globular
cluster M15; following KR, I adopt an upper limit of
M
(Maiolino et al. 1998).
The last upper limit shown in the figure pertains to the globular
cluster M15; following KR, I adopt an upper limit of
M = 1
× 103
M
= 1
× 103
M .
.
However, before reading too much into this diagram, we should ask whether
the apparent correlation might arise from selection effects.
The absence of points on the upper left-hand corner is probably real;
there is nothing preventing us from detecting a massive BH in a
small galaxy. Yet, we should be cautious, because very few low-mass
galaxies have been studied so far, most of the effort having been
focused on luminous, early-type systems. On the other hand, the empty
region on the lower right-hand corner could be an artifact. Small
masses are difficult to detect at large distances, and most luminous
galaxies are far away. So the apparent correlation could be
an upper envelope. Future observations are needed to settle this issue.
The median value of
M /
LB(bul) for the 20 detected
objects is 0.012, which translates into a mass ratio of 0.002 for
M / LB
/
LB(bul) for the 20 detected
objects is 0.012, which translates into a mass ratio of 0.002 for
M / LB
 6 typical for old
stellar populations
(van der Marel 1991).
That is, on average about 0.2% of the bulge mass is locked up in the form
of a SMBH.
Magorrian et al. (1998)
constructed axisymmetric f (E, Lz)
models for a sample of 32 early-type (mostly E and S0) galaxies having both
HST photometry and ground-based stellar kinematics data, and they
concluded that the data are consistent with nearly all of the galaxies
having SMBHs. The 29 detected objects have a median
M
6 typical for old
stellar populations
(van der Marel 1991).
That is, on average about 0.2% of the bulge mass is locked up in the form
of a SMBH.
Magorrian et al. (1998)
constructed axisymmetric f (E, Lz)
models for a sample of 32 early-type (mostly E and S0) galaxies having both
HST photometry and ground-based stellar kinematics data, and they
concluded that the data are consistent with nearly all of the galaxies
having SMBHs. The 29 detected objects have a median
M /
Mbul
/
Mbul
 0.005, higher than found
here. However, as
Magorrian et al. realize, the assumption of a two-integral distribution
function may have caused them to overestimate
M
0.005, higher than found
here. However, as
Magorrian et al. realize, the assumption of a two-integral distribution
function may have caused them to overestimate
M (cf.
van der Marel 1999).
Interestingly, quasars possibly also obey a similar
M
(cf.
van der Marel 1999).
Interestingly, quasars possibly also obey a similar
M -Mbul relation.
McLeod (1998)
finds that, for the most
luminous quasars, there exists a minimum host luminosity that increases
with nuclear power. Assuming that the quasar luminosities correspond to
energy generation at the Eddington rate,
M
-Mbul relation.
McLeod (1998)
finds that, for the most
luminous quasars, there exists a minimum host luminosity that increases
with nuclear power. Assuming that the quasar luminosities correspond to
energy generation at the Eddington rate,
M /
Mbul is again ~ 0.002
(McLeod 1998).
/
Mbul is again ~ 0.002
(McLeod 1998).
With regard to the dead quasar prediction discussed in
Section 1, recall that
we expect to find on average a 107
M BH for every
LB
BH for every
LB  1010 L
1010 L galaxy, or
M
galaxy, or
M /
LB(bul)
/
LB(bul)
 3.3 ×
10-3
M
3.3 ×
10-3
M /
L
/
L since bulges
contribute typical 30% of
the galaxy light in B
(Schechter & Dressler
1987).
Evidently, if
since bulges
contribute typical 30% of
the galaxy light in B
(Schechter & Dressler
1987).
Evidently, if
 = 0.1, we have already
found about three times that value. This implies that either
= 0.1, we have already
found about three times that value. This implies that either
 is smaller than 0.1, or
that quasars do not make up all of the AGN population.
is smaller than 0.1, or
that quasars do not make up all of the AGN population.
8. ARE SUPERMASSIVE BLACK HOLES UBIQUITOUS?
They certainly have not been found in every case that has been looked.
Kormendy has undertaken a systematic survey of a modest sample of galaxies
(E-Sb), and his detection rate has been about 20% (KR). But, of
course, many factors conspire against the detection of MDOs, and this
estimate should be regarded as firm lower limit. If one takes seriously the
M -
Mbul relation described above, it is possible that
every bulge contains a SMBH with an appropriately scaled size. This
view is supported by the statistical analysis of
Magorrian et al. (1998).
In fact, the detection of an MDO in NGC 4945
(Section 4.2) and the presence of a
bona fide AGN in NGC 4395 indicate that perhaps even some galaxies
without bulges may have SMBHs.
-
Mbul relation described above, it is possible that
every bulge contains a SMBH with an appropriately scaled size. This
view is supported by the statistical analysis of
Magorrian et al. (1998).
In fact, the detection of an MDO in NGC 4945
(Section 4.2) and the presence of a
bona fide AGN in NGC 4395 indicate that perhaps even some galaxies
without bulges may have SMBHs.

|
Figure 9. (a) Detection rate and
(b) number distribution of AGNs
as a function of Hubble type in the spectroscopic survey of
Ho et al. (1995,
1997).
"Type 1" AGNs (those with broad
H ) are shown separately
from the total population (types 1 and 2). ) are shown separately
from the total population (types 1 and 2).
|
Additional support for this picture comes from the growing evidence that
nonstellar nuclear activity is very common in galaxies, much more so than
conventionally believed based on the statistics of bright AGNs and quasars.
A recent spectroscopic survey of a large, statistically complete sample of
nearby galaxies finds that over 40% of all bright
(BT  12.5 mag)
galaxies have nuclei that can be classified as "active," and the percentage
is even higher among early-type systems (E-Sbc), approaching 50%-75%
(Ho, Filippenko, & Sargent
1997).
Most of the nearby AGNs have much
lower luminosities than traditionally studied active galaxies, and a
greater heterogeneity in spectral types is found (low-ionization nuclei, or
LINERs, are common, for example), but the evidence is overwhelming that
many of these nuclei are truly accretion-powered sources (see
Filippenko 1996;
Ho et al. 1997).
Moreover, intrinsically weak, compact
radio cores are known to be present in a significant fraction of elliptical
and S0 galaxies
(Sadler, Jenkins, & Kotanyi
1989;
Wrobel & Heeschen 1991),
almost all of which spectroscopically qualify as AGNs
(Ho 1998).
12.5 mag)
galaxies have nuclei that can be classified as "active," and the percentage
is even higher among early-type systems (E-Sbc), approaching 50%-75%
(Ho, Filippenko, & Sargent
1997).
Most of the nearby AGNs have much
lower luminosities than traditionally studied active galaxies, and a
greater heterogeneity in spectral types is found (low-ionization nuclei, or
LINERs, are common, for example), but the evidence is overwhelming that
many of these nuclei are truly accretion-powered sources (see
Filippenko 1996;
Ho et al. 1997).
Moreover, intrinsically weak, compact
radio cores are known to be present in a significant fraction of elliptical
and S0 galaxies
(Sadler, Jenkins, & Kotanyi
1989;
Wrobel & Heeschen 1991),
almost all of which spectroscopically qualify as AGNs
(Ho 1998).
Within the conventional AGN paradigm, the observed widespread nuclear
activity implies that SMBHs are a generic component of many, perhaps most,
present-day bulge-dominated galaxies, consistent with the picture emerging
from the kinematic studies. This is a remarkable statement. It implies
that SMBHs should not be regarded as "freaks of nature" that
exist in only a handful of galaxies; rather, they must be accepted and
understood as a normal component of galactic structure, one that arises
naturally in the course of galaxy formation and evolution.
9. SOME IMPLICATIONS AND FUTURE DIRECTIONS
The SMBH hunting game is rapidly becoming a rather mature subject. I think
we have progressed from the era of "the thrill of discovery" to a point
where we are on the verge of using SMBHs as astrophysical tools. In this
spirit, let me remark on a few of the ramifications of the existing
observations and point out some of the more urgent directions that should
be pursued.
A. The
M -Mbul relation.
The apparent correlation between the mass of the central BH and the
mass of the bulge, if borne out by future scrutiny, has significant
implications (see below). From an observational point of view, the highest
immediate priority is to populate the
M
-Mbul relation.
The apparent correlation between the mass of the central BH and the
mass of the bulge, if borne out by future scrutiny, has significant
implications (see below). From an observational point of view, the highest
immediate priority is to populate the
M -Mbul
diagram with objects spanning a wide range in luminosity, with the eventual
aim of deriving a mass function for SMBHs. The samples should
be chosen with the following questions in mind. (1) Is the apparent trend a
true correlation or does it instead trace an upper envelope? (2) If the
relation is real, is it linear? (3) What is the magnitude of the intrinsic
scatter? And (4) is there a minimum bulge luminosity (mass) below which
SMBHs do not exist?
-Mbul
diagram with objects spanning a wide range in luminosity, with the eventual
aim of deriving a mass function for SMBHs. The samples should
be chosen with the following questions in mind. (1) Is the apparent trend a
true correlation or does it instead trace an upper envelope? (2) If the
relation is real, is it linear? (3) What is the magnitude of the intrinsic
scatter? And (4) is there a minimum bulge luminosity (mass) below which
SMBHs do not exist?
In the near future, the most efficient way to obtain mass measurements for
relatively large numbers of galaxies is to exploit the capabilities of STIS
on HST. Several large programs are in progress. Although VLBI
spectroscopy of H2O masers delivers much higher angular
resolution, this
technique is limited by the availability of suitably bright
sources. Conditions
which promote H2O megamaser emission evidently are realized
in only a tiny fraction of galaxies
(Braatz, Wilson, & Henkel
1996).
B. The formation of SMBHs.
The M -Mbul relation offers some clues to
the formation mechanism of SMBHs. How does a galaxy know how to extract a
constant, or at least a limiting, fraction of its bulge mass into a SMBH?
An attractive possibility is by the normal dynamical evolution of the
galaxy core itself. The spheroidal component of nearby galaxies can attain
very high central stellar densities - up to 105
M
-Mbul relation offers some clues to
the formation mechanism of SMBHs. How does a galaxy know how to extract a
constant, or at least a limiting, fraction of its bulge mass into a SMBH?
An attractive possibility is by the normal dynamical evolution of the
galaxy core itself. The spheroidal component of nearby galaxies can attain
very high central stellar densities - up to 105
M pc-3
(Faber et al. 1997)
- and some with distinct nuclei have even higher
concentrations still
(Lauer et al. 1995).
Although most galaxy cores are
unlikely to have experienced dynamical collapse
(Kormendy 1988c),
the innermost regions have much shorter relaxation times,
especially when considering a realistic stellar mass spectrum because
the segregation of the
most massive stars toward the center greatly accelerates the dynamical
evolution of the system. Lee
(1995,
and these proceedings) shows that, under
conditions typical of galactic nuclei, core collapse and merging of
stellar-size BHs can easily form a seed BH of moderate mass.
Alternatively, the seed object may form via
the catastrophic collapse of a relativistic cluster of compact remnants
(Quinlan & Shapiro 1990).
In either case, subsequent accretion of gas and
stars will augment the central mass, and, over a Hubble time, may
produce the
distribution of masses observed. It is far too premature to tell whether
SMBHs form through the secular evolution of galaxies, as suggested here,
through processes associated with the initial formation of galaxies
(e.g.,
Rees 1984,
1998;
Silk & Rees 1998),
or both, depending on the galaxy
type (elliptical vs. spiral galaxies). But the stage is set for a serious
discussion. More sophisticated modeling of the growth of SMBHs that take
into account a wider range of initial conditions in galactic nuclei
(e.g., relaxing the adiabatic assumption or adopting more realistic
density profiles for the
stellar distribution) may eventually yield testable predictions (see, e.g.,
Stiavelli 1998).
pc-3
(Faber et al. 1997)
- and some with distinct nuclei have even higher
concentrations still
(Lauer et al. 1995).
Although most galaxy cores are
unlikely to have experienced dynamical collapse
(Kormendy 1988c),
the innermost regions have much shorter relaxation times,
especially when considering a realistic stellar mass spectrum because
the segregation of the
most massive stars toward the center greatly accelerates the dynamical
evolution of the system. Lee
(1995,
and these proceedings) shows that, under
conditions typical of galactic nuclei, core collapse and merging of
stellar-size BHs can easily form a seed BH of moderate mass.
Alternatively, the seed object may form via
the catastrophic collapse of a relativistic cluster of compact remnants
(Quinlan & Shapiro 1990).
In either case, subsequent accretion of gas and
stars will augment the central mass, and, over a Hubble time, may
produce the
distribution of masses observed. It is far too premature to tell whether
SMBHs form through the secular evolution of galaxies, as suggested here,
through processes associated with the initial formation of galaxies
(e.g.,
Rees 1984,
1998;
Silk & Rees 1998),
or both, depending on the galaxy
type (elliptical vs. spiral galaxies). But the stage is set for a serious
discussion. More sophisticated modeling of the growth of SMBHs that take
into account a wider range of initial conditions in galactic nuclei
(e.g., relaxing the adiabatic assumption or adopting more realistic
density profiles for the
stellar distribution) may eventually yield testable predictions (see, e.g.,
Stiavelli 1998).
C. Influence of SMBHs on galactic structure.
Norman, May, & Van Albada
(1985)
showed through N-body simulations that a massive singularity in
the center of a triaxial galaxy destroys the box-like stellar orbits and
hence can erase the nonaxisymmetry, at least on small scales. This has
several important consequences. First, it implies that the presence of a
SMBH can influence the global structure and dynamics of galaxies.
Second, the secular evolution of the axisymmetry of the central potential
points to a natural mechanism for galaxies to self-regulate the transfer of
angular momentum of the gas from large to small scales. This
negative-feedback
process may limit the growth of the central BH and the
accretion rate onto it, and hence may serve as a promising framework for
understanding the physical evolution of AGNs.
Merritt & Quinlan (1998)
find that the timescale for effecting the transition from triaxiality
to axisymmetry depends strongly on the fractional mass of the BH;
the evolution occurs rapidly when
M / Mbul
/ Mbul
 2.5%,
remarkably close to the observational upper limit
(Fig. 8 a).
2.5%,
remarkably close to the observational upper limit
(Fig. 8 a).
D. The origin of central cores. It is not
understood why giant ellipticals have such shallow central light profiles.
"Cores" do not develop naturally in popular scenarios of structure
formation, and even if they form, they are difficult to maintain against
the subsequent acquisition of the dense, central regions of satellite
galaxies that get accreted
(Faber et al. 1997).
Moreover, the very presence of a SMBH,
whether it grew adiabatically in a preexisting stellar system or the
galaxy formed by violent relaxation around it
(Stiavelli 1998),
ought to imprint a more sharply cusped light profile (see
Section 2) than is observed.
An intriguing possibility is that cores were created as a result of
mergers, where one or more of the galaxies contains a BH. As the single
(Nakano & Makino 1998)
or binary
(Makino 1997;
Quinlan & Hernquist 1997)
BH sinks toward the center of the remnant due to dynamical friction, it
heats the stars, thereby producing a "fluffy" core. If this
interpretation is correct, it would provide a simple, powerful tool to
diagnose the formation history of galaxies.
E. Why are the black holes so black?
It has been somewhat puzzling how the BHs can remain so
dormant. No doubt the dwindled gas supply in the present epoch, especially
in ellipticals, is largely responsible for the inactivity. Yet the accretion
rate cannot be zero; even in the absence of inflow from the general
interstellar medium, some gas is shed through normal mass loss from the
innermost evolved stars, and occasionally such stars get tidally disrupted
(see below). If
SMBHs are indeed present, the radiative efficiency of the accretion flow
must be orders of magnitude lower than that of "standard" optically thick,
geometrically thin disks. Such a situation may be realized in accretion
flows where advection becomes important when the accretion rate is highly
sub-Eddington
(Narayan & Yi 1995;
Abramowicz et al. 1995;
Nakamura et al. 1996;
Chakrabarti 1996).
Sgr A* at the Galactic Center has a bolometric
luminosity of only ~ 1037 ergs s-1, or
Lbol / LEdd
 3 × 10-8
(Narayan, Yi, & Mahadevan
1995);
in the case of the LINER nucleus of M81
(Ho, Filippenko, & Sargent
1996),
Lbol
3 × 10-8
(Narayan, Yi, & Mahadevan
1995);
in the case of the LINER nucleus of M81
(Ho, Filippenko, & Sargent
1996),
Lbol  1041 ergs s-1 and
Lbol / LEdd
1041 ergs s-1 and
Lbol / LEdd
 10-4. The
spectral energy distributions emitted by both objects differ
dramatically from those of
luminous AGNs and can be approximately matched by advective-disk models.
10-4. The
spectral energy distributions emitted by both objects differ
dramatically from those of
luminous AGNs and can be approximately matched by advective-disk models.
F. Tidal disruption of stars.
The prevalence of SMBHs suggested by the existing evidence predicts a
relatively high incidence of tidal disruptions of stars as they scatter
into nearly radial orbits whose pericenters pass within the tidal radius
of the BH
(Rees 1998,
and references therein). For a typical stellar
density of 105 stars pc-3,
M =
106-108
M
=
106-108
M ,
and
,
and  = 100-300 km
s-1, a solar-type star will be disrupted once
every 102-104 years. (BHs more massive than
108
M
= 100-300 km
s-1, a solar-type star will be disrupted once
every 102-104 years. (BHs more massive than
108
M will swallow the star whole.) Roughly half the debris becomes unbound and
half gets captured into an accretion disk which undergoes a bright flare
(~ 1010
L
will swallow the star whole.) Roughly half the debris becomes unbound and
half gets captured into an accretion disk which undergoes a bright flare
(~ 1010
L ) lasting a few
months to a year. The spectrum is
expected to be mainly thermal and to peak in the extreme-UV and soft
X-rays. The contribution to the near-UV and optical bands is uncertain;
it depends on assumptions concerning the geometry of the accretion disk
(thick or thin) and
on whether an optically thick envelope can form. For plausible parameters,
Ulmer (1998)
estimates that a 107
M
) lasting a few
months to a year. The spectrum is
expected to be mainly thermal and to peak in the extreme-UV and soft
X-rays. The contribution to the near-UV and optical bands is uncertain;
it depends on assumptions concerning the geometry of the accretion disk
(thick or thin) and
on whether an optically thick envelope can form. For plausible parameters,
Ulmer (1998)
estimates that a 107
M BH will produce a
flare
with an absolute magnitude of about -20 in U and -18.5 in V.
The realization that SMBHs may be even more common than previously thought
provides fresh motivation to search for such stellar flares; some
observational strategies are mentioned by
Rees (1998).
Here, I wish to stress that
quantifying the rate of stellar disruptions can be used as a tool to study
the demography of SMBHs out to relatively large distances and hence
should be regarded as complementary to the kinematic searches.
BH will produce a
flare
with an absolute magnitude of about -20 in U and -18.5 in V.
The realization that SMBHs may be even more common than previously thought
provides fresh motivation to search for such stellar flares; some
observational strategies are mentioned by
Rees (1998).
Here, I wish to stress that
quantifying the rate of stellar disruptions can be used as a tool to study
the demography of SMBHs out to relatively large distances and hence
should be regarded as complementary to the kinematic searches.
Acknowledgements
I am grateful to S. K. Chakrabarti for the invitation to participate in
this workshop and his help in arranging a pleasurable visit to India. I
thank G. A. Bower, S. Collier, R. Genzel, L. J. Greenhill, J. Kormendy,
R. Maiolino,
D. Maoz, E. Maoz, and K. Nandra for contributing to, or for providing
comments that have improved the presentation of, the material in this
paper. This work was supported by a postdoctoral fellowship from the
Harvard-Smithsonian Center for Astrophysics and by NASA grants
from the Space Telescope Science Institute (operated by AURA, Inc., under
NASA contract NAS 5-26555).
REFERENCES
Abramowicz, M. A., Chen, X., Kato, S., Lasota, J.-P., & Regev, O.
1995, ApJ, 438, L37
Bahcall, J. N., & Wolf, R. A.
1976, ApJ, 209, 214
Bender, R., Burstein, D., & Faber, S. M.
1992, ApJ, 399, 462
Binney, J., & Mamon, G. A.
1982, MNRAS, 200, 361
Blandford, R. D., & McKee, C. F.
1982, ApJ, 255, 419
Blandford, R. D., & Rees, M. J. 1992, in
Testing the AGN Paradigm, ed.
S. Holt, S. Neff, & M. Urry (New York: AIP), 3
Bower, G. A., et al.
1998, ApJ, 492, L111
Bower, G. A., Wilson, A. S., Heckman, T. M., & Richstone, D. O.
1996, in
The Physics of LINERs in View of Recent Observations, ed. M. Eracleous
et al. (San Francisco: ASP), 163
Braatz, J. A., Wilson, A. S., & Henkel, C.
1996, ApJS, 106, 51
Carollo, C. M., Franx, M., Illingworth, G. D., & Forbes, D. A.
1997, ApJ, 481, 710
Chakrabarti, S. K.
1995, ApJ, 441, 576
Chakrabarti, S. K.
1996, ApJ, 464, 664
Chokshi, A., & Turner, E. L.
1992, MNRAS, 259, 421
Claussen, M. J., & Lo, K.-Y.
1986, ApJ, 308, 592
Crane, P., et al.
1993, AJ, 106, 1371
Cretton, N., de Zeeuw, P. T., van der Marel, R. P., & Rix, H.-W.
1999, ApJS, 124, 383
Dehnen, W.
1995, MNRAS, 274, 919
de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., Buta, R. J.,
Paturel, G., & Fouqué, R. 1991,
Third Reference Catalogue of Bright
Galaxies (New York: Springer) (RC3)
Devereux, N. A., Ford, H. C., & Jacoby, G.
1997, ApJ, 481, L71
Dibai, E. A.
1980, Soviet Astron., 24, 389
Dressler, A., & Richstone, D. O.
1988, ApJ, 324, 701
Dressler, A., & Richstone, D. O.
1990, ApJ, 348, 120
Duncan, M. J., & Wheeler, J. C.
1980, ApJ, 237, L27
Eckart, A., & Genzel, R.
1996, Nature, 383, 415
Eckart, A., & Genzel, R.
1997, MNRAS, 284, 576
Eracleous, M., Halpern, J. P., Gilbert, A. M., Newman, J. A., &
Filippenko, A. V.
1997, ApJ, 490, 216
Faber, S. M., et al. 1987, in
Nearly Normal Galaxies, ed. S. M. Faber (New York:
Springer), 175
Faber, S. M., et al.
1997, AJ, 114, 1771
Fabian, A. C., Nandra, K., Reynolds, C. S., Brandt, W. N., Otani, C.,
Tanaka, Y., Inoue, H., & Iwasawa, K.
1995, MNRAS, 277, L11
Fabian, A. C., Rees, M. J., Stella, L., & White, N. E.
1989, MNRAS, 238, 729
Ferrarese, L., Ford, H. C., & Jaffe, W.
1996, ApJ, 470, 444
Ferrarese, L., Ford, H. C., & Jaffe, W.
1998, ApJ, in press
Filippenko, A. V. 1996, in
The Physics of LINERs in View
of Recent Observations, ed. M. Eracleous et al. (San Francisco: ASP), 17
Filippenko, A. V., & Ho, L. C.
1998, ApJ, submitted
Filippenko, A. V., Ho, L. C., & Sargent, W. L. W.
1993, ApJ, 410, L75
Fillmore, J. A., Boroson, T. A., & Dressler, A.
1986, ApJ, 302, 208
Ford, H. C., et al.
1994, ApJ, 435, L27
Ford, H. C., Tsvetanov, Z. I., Ferrarese, L., & Jaffe, W. 1998, in
IAU Symp. 184, The Central Regions of the Galaxy and
Galaxies,
ed. Y. Sofue (Dordrecht: Kluwer), p. 377
Gebhardt, K., et al.
1998, AJ, in press
Genzel, R., Eckart, A., Ott, T., & Eisenhauer, F.
1997, MNRAS, 291, 219
Genzel, R., Thatte, N., Krabbe, A., Kroker, H., & Tacconi-Garman,
L. E.
1996, ApJ, 472, 153
Gerhard, O. E.
1993, MNRAS, 265, 213
Ghez, A. M., et al. 1998, in
IAU Symp. 184, The Central Regions of the
Galaxy and Galaxies, ed. Y. Sofue (Dordrecht: Kluwer), p. 433
Goodman, J., & Lee, H. M.
1989, ApJ, 337, 84
Greenhill, L. J. 1997, in
IAU Colloq. 159, Emission Lines in Active Galaxies:
New Methods and Techniques, ed. B. M. Peterson, F.-Z. Cheng, &
A. S. Wilson (San Francisco: ASP), 394
Greenhill, L. J. 1998, in
IAU Colloq. 164, Radio Emission from Galactic and
Extragalactic Compact Sources, ed. A. Zensus, G. Taylor, & J. Wrobel
(San Francisco: ASP), p. 221
Greenhill, L. J., Gwinn, C. R., Antonucci, R., & Barvainis, R.
1996, ApJ, 472, L21
Greenhill, L. J., Moran, J. M., & Herrnstein, J. R.
1997, ApJ, 481, L23
Harms, R. J., et al.
1994, ApJ, 435, L35
Ho, L. C.
1998, ApJ, submitted
Ho, L. C., et al.
1998, in preparation
Ho, L. C., Filippenko, A. V., & Sargent, W. L. W.
1995, ApJS, 98, 477
Ho, L. C., Filippenko, A. V., & Sargent, W. L. W.
1996, ApJ, 462, 183
Ho, L. C., Filippenko, A. V., & Sargent, W. L. W.
1997, ApJ, 487, 568
Jaffe, W., Ford, H. C., Ferrarese, L., van den Bosch, F., &
O'Connell, R. W.
1993, Nature, 364, 213
Jaffe, W., et al.
1994, AJ, 108, 1567
Jones, D. H., et al.
1996, ApJ, 466, 742
Kormendy, J.
1988a, ApJ, 325, 128
Kormendy, J.
1988b, ApJ, 335, 40
Kormendy, J. 1988c, in
Supermassive Black Holes, ed. M. Kafatos (Cambridge:
Cambridge Univ. Press), 219
Kormendy, J. 1993, in
The Nearest Active Galaxies, ed. J. Beckman, L. Colina,
& H. Netzer (Madrid: CSIC Press), 197
Kormendy, J., et al.
1996, ApJ, 459, L57
Kormendy, J., et al.
1997a, ApJ, 473, L91
Kormendy, J., et al.
1997b, ApJ, 482, L139
Kormendy, J., Bender, R., Evans, A. S., & Richstone, D.
1998, AJ, 115, 1823
Kormendy, J., & McClure, R. D.
1993, AJ, 105, 1793
Kormendy, J., & Richstone, D. O.
1995, ARA&A, 33, 581 (KR)
Krabbe, A., et al.
1995, ApJ, 447, L95
Krolik, J. H. 1997, in
IAU Colloq. 159, Emission Lines in Active Galaxies:
New Methods and Techniques, ed. B. M. Peterson, F.-Z. Cheng, &
A. S. Wilson (San Francisco: ASP), 459
Lacy, J. H., Townes, C. H., Geballe, T. R., & Hollenbach, D. J.
1980, ApJ, 241, 132
Lauer, T. R., et al.
1992, AJ, 103, 703
Lauer, T. R., et al.
1995, AJ, 110, 2622
Lee, H. M.
1995, MNRAS, 272, 605
Lin, H., et al.
1996, ApJ, 464, 60
Lynden-Bell, D.
1969, Nature, 223, 690
Lynden-Bell, D., & Rees, M. J.
1971, MNRAS, 152, 461
Macchetto, F., Marconi, A., Axon, D. J., Capetti, A., Sparks, W. B., &
Crane, P.
1997, ApJ, 489, 579
Magorrian, J., et al.
1998, AJ, in press
Maiolino, R., Krabbe, A., Thatte, N., & Genzel, R.
1998, ApJ, 493, 650
Makino, F.
1997, ApJ, 478, 58
Maoz, E.
1995, ApJ, 447, L91
Maoz, E.
1998, ApJ, 494, L181
McLeod, K. K. 1998, in
Quasar Hosts, ed. D. Clements & I. Perez-Fournon
(Berlin: Springer-Verlag), in press
Menou, K., Quataert, E., & Narayan, R. 1999, in
Proc. of the 8th Marcel
Grossmann Meeting on General Relativity (Jerusalem), p. 204
Merritt, D., & Quinlan, G.
1998, ApJ, in press
Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., Nakai, N.,
Diamond, P., & Inoue, M.
1995, Nature, 373, 127
Moran, E. C., Filippenko, A. V., Ho, L. C., Belloni, T., Shields,
J. C., Snowden, S. L., & Sramek, R. A.
1999, PASP, 111, 801
Nakai, N., Inoue, M., & Miyoshi, M.
1993, Nature, 361, 45
Nakamura, K. E., Matsumoto, R., Kusunose, M., & Kato, S.
1996, PASJ, 48, 761
Nakano, T., & Makino, J.
1998, ApJ, in press
Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T.
1997, ApJ, 477, 602
Narayan, R., & Yi, I.
1995, ApJ, 452, 710
Narayan, R., Yi, I., & Mahadevan, R.
1995, Nature, 374, 623
Netzer, H., & Peterson, B. M. 1997, in
Astronomical Time Series, ed.
D. Maoz, A. Sternberg, & E. M. Leibowitz (Dordrecht: Kluwer), 85
Newman, J. A., Eracleous, M., Filippenko, A. V., & Halpern, J. P.
1997, ApJ, 485, 570
Nieto, J.-L., Bender, R., Arnaud, J., & Surma, P.
1991, A&A, 244, L37
Norman, C. A., May, A., & Van Albada, T. S.
1985, ApJ, 296, 20
Padovani, P., Burg, R., & Edelson, R. A.
1990, ApJ, 353, 438
Peebles, P. J. E.
1972, ApJ, 178, 371
Peterson, B. M., Wanders, I., Bertram, R., Hunley, J. F., Pogge, R. W.,
& Wagner, R. M.
1998, ApJ, in press
Pounds, K., Nandra, K., Stewart, G. C., George, I. M., & Fabian, A. C.
1990, Nature, 344, 132
Qian, E. E., de Zeeuw, P. T., van der Marel, R. P., & Hunter, C.
1995, MNRAS, 274, 602
Quinlan, G. D., & Hernquist, L.
1997, New Astron., 2(6), 533
Quinlan, G. D., Hernquist, L., & Sigurdsson, S.
1995, ApJ, 440, 554
Quinlan, G. D., & Shapiro, S. L.
1990, ApJ, 356, 483
Rees, M. J.
1984, ARA&A, 22, 471
Rees, M. J. 1998, in
Proc. Chandrasekhar Memorial Conf., Black Holes and
Relativity, ed. R. Wald (Chicago: Chicago Univ. Press), in press
Reynolds, C. S., & Begelman, M. C.
1997, ApJ, 488, 109
Richstone, D. O. 1998, in
IAU Symp. 184, The Central Regions of the Galaxy and
Galaxies, ed. Y. Sofue (Dordrecht: Kluwer), p. 451
Richstone, D. O., Bower, G., & Dressler, A.
1990, ApJ, 353, 118
Richstone, D. O., & Tremaine, S.
1984, ApJ, 286, 27
Richstone, D. O., & Tremaine, S.
1985, ApJ, 296, 370
Richstone, D. O., & Tremaine, S.
1988, ApJ, 327, 82
Rybicki, G. B., & Bromley, B. C.
1998, ApJ, in press
Sadler, E. M., Jenkins, C. R., & Kotanyi, C. G.
1989, MNRAS, 240, 591
Salpeter, E. E.
1964, ApJ, 140, 796
Sargent, W. L. W., Young, P. J., Boksenberg, A., Shortridge, K., Lynds,
C. R., & Hartwick, F. D. A.
1978, ApJ, 221, 731
Schechter, P. L., & Dressler, A.
1987, AJ, 94, 563
Silk, J., & Rees, M. J.
1998, A&A, 331, L1
Simien, F., & de Vaucouleurs, G.
1986, ApJ, 302, 564
Soltan, A.
1982, MNRAS, 200, 115
Stiavelli, M.
1998, ApJ, 495, L91
Tanaka, Y., et al.
1995, Nature, 375, 659
Titarchuk, L., & Zannias, T.
1998, ApJ, 493, 863
Trotter, A. S., Greenhill, L. J., Moran, J. M., Reid, M. J., Irwin, J. A.,
& Lo, K.-Y.
1998, ApJ, 495, 740
Tully, R. B. 1988,
Nearby Galaxies Catalog (Cambridge: Cambridge
Univ. Press)
Ulmer, A. 1998, ApJ, in press
van den Bosch, F. C. 1998, in
IAU Symp. 184, The Central Regions of the Galaxy
and Galaxies, ed. Y. Sofue (Dordrecht: Kluwer), p. 387
van den Bosch, F. C., Jaffe, W., & van der Marel, R. P.
1998, MNRAS, 293, 343
van der Marel, R. P.
1991, MNRAS, 253, 710
van der Marel, R. P.
1994a, MNRAS, 270, 271
van der Marel, R. P.
1994b, ApJ, 432, L91
van der Marel, R. P. 1999, in
IAU Symp. 186, Galaxy Interactions at Low
and High Redshift, ed. D. B. Sanders & J. Barnes (Dordrecht:
Kluwer), p. 333
van der Marel, R. P., Cretton, N., de Zeeuw, P. T., & Rix, H.-W.
1998, ApJ, 493, 613
van der Marel, R. P., de Zeeuw, P. T., Rix, H.-W., & Quinlan, G. D.
1997, Nature, 385, 610
van der Marel, R. P., Evans, N. W., Rix, H.-W., White, S. D. M., &
de Zeeuw, P. T.
1994a, MNRAS, 271, 99
van der Marel, R. P., Rix, H.-W., Carter, D., Franx, M., White,
S. D. M., & de Zeeuw, P. T.
1994b, MNRAS, 268, 521
Wandel, A., & Mushotzky, R. F.
1986, ApJ, 306, L61
Wandel, A., & Yahil, A.
1985, ApJ, 295, L1
Watson, W. D., & Wallin, B. K.
1994, ApJ, 432, L35
Wrobel, J. M., & Heeschen, D. S.
1991, AJ, 101, 148
Young, P. J.
1980, ApJ, 242, 1232
Young, P. J., Westphal, J. A., Kristian, J., Wilson, C. P., &
Landauer, F. P.
1978, ApJ, 221, 721
Zel'dovich, Ya. B., & Novikov, I. D.
1964, Sov. Phys. Dokl., 158, 811
 MOTIVATION
MOTIVATION
 EARLY CLUES FROM PHOTOMETRY
EARLY CLUES FROM PHOTOMETRY
 METHODS BASED ON STELLAR KINEMATICS
METHODS BASED ON STELLAR KINEMATICS
 METHODS BASED ON GAS KINEMATICS
METHODS BASED ON GAS KINEMATICS
 Optical Emission Lines
Optical Emission Lines
 Radio Spectroscopy of Water Masers
Radio Spectroscopy of Water Masers
 Determining Central Masses of Active Galactic
Nuclei
Determining Central Masses of Active Galactic
Nuclei
 INDIRECT, BUT TANTALIZING EVIDENCE
INDIRECT, BUT TANTALIZING EVIDENCE
 ARE THE MASSIVE DARK OBJECTS REALLY BLACK
HOLES?
ARE THE MASSIVE DARK OBJECTS REALLY BLACK
HOLES?
 THE BLACK-HOLE MASS/BULGE MASS RELATION
THE BLACK-HOLE MASS/BULGE MASS RELATION
 ARE SUPERMASSIVE BLACK HOLES UBIQUITOUS?
ARE SUPERMASSIVE BLACK HOLES UBIQUITOUS?
 SOME IMPLICATIONS AND FUTURE DIRECTIONS
SOME IMPLICATIONS AND FUTURE DIRECTIONS
 REFERENCES
REFERENCES
 106 - 109
M
106 - 109
M . Since then this
model has provided a highly useful framework for the study of quasars, or
more generally, of the active galactic nucleus (AGN) phenomenon
(
. Since then this
model has provided a highly useful framework for the study of quasars, or
more generally, of the active galactic nucleus (AGN) phenomenon
(

 0.1-1
M
0.1-1
M 107
107 GM
GM 2
(
2
( r-3/2
(
r-3/2
( , with
, with
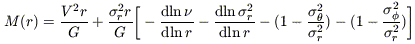
 and
and
 the azimuthal components of
the velocity dispersion, and
the azimuthal components of
the velocity dispersion, and  is
the density of the tracer population.
In practice, several simplifying assumptions are adopted: (1) the mass
distribution is spherically symmetric; (2) the mean rotation is circular;
and (3)
is
the density of the tracer population.
In practice, several simplifying assumptions are adopted: (1) the mass
distribution is spherically symmetric; (2) the mean rotation is circular;
and (3)  + 1,
it is apparent that, under suitable conditions, all four terms can largely
cancel one another. As emphasized by KR, all else being equal, smaller,
lower luminosity galaxies such as
+ 1,
it is apparent that, under suitable conditions, all four terms can largely
cancel one another. As emphasized by KR, all else being equal, smaller,
lower luminosity galaxies such as 
 100;
the dark mass must have a density in excess of 109
M
100;
the dark mass must have a density in excess of 109
M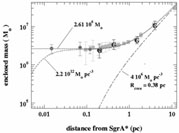



 line
displayed sinusoidal variations with a period of 2.2 years for several
years
(
line
displayed sinusoidal variations with a period of 2.2 years for several
years
(
 1%). The
implied binding mass within 0.13 pc is 3.6 × 107
M
1%). The
implied binding mass within 0.13 pc is 3.6 × 107
M
 v2rBLR / G, where
v2rBLR / G, where

 3 / 2)FWHM, the full width at
half-maximum of a
representative broad line. Yet another ambiguity is which line to use,
since not all broad emission lines have the same widths. Ultraviolet or
high-ionization lines, for instance, generally have broader profiles than
optical or low-ionization lines. For the purposes of this exercise, I
simply chose the line for which the most data exist
(H
3 / 2)FWHM, the full width at
half-maximum of a
representative broad line. Yet another ambiguity is which line to use,
since not all broad emission lines have the same widths. Ultraviolet or
high-ionization lines, for instance, generally have broader profiles than
optical or low-ionization lines. For the purposes of this exercise, I
simply chose the line for which the most data exist
(H ) in order to obtain
as large a sample as possible.
) in order to obtain
as large a sample as possible.