2. BLACK HOLE MASS ESTIMATES: A CRITICAL REVIEW

Epimetheus: Wie vieles ist denn dein?
Prometheus: Der Kreis, den meine Wirksamkeit erfüllt!

Epimetheus: What then do you possess?
Prometheus: My sphere of influence - nothing more and nothing less!

Goethe, Prometheus

2.1. A Discrepancy, and its Resolution

By 1999, a clear discrepancy was emerging between black hole masses derived from stellar kinematical studies and most other techniques. The former sample included many "standard bearers" like M31 (Richstone, Bower & Dressler 1990), NGC 3115 (Kormendy et al. 1996a) and NGC 4594 (Kormendy et al. 1996b). The size of the discrepancy was difficult to pin down since there were (and still are) essentially no galaxies for which black hole masses had been independently derived using more than one technique. However the masses derived from ground-based stellar kinematics were much larger, by roughly an order of magnitude on average, than those inferred from other techniques when galaxies with similar properties were compared, or when estimates of the cosmological density of black holes or the mean ratio of black hole mass to bulge mass were made. The discrepancy was clearest in two arenas:

• Active vs. Quiescent Galaxies. In Seyfert galaxies, the gravitational influence of the black hole can be measured on small scales, ~ 10^-2 pc, using emission lines from the broad emission line region (BLR). The technique of "reverberation mapping" combines the velocity of the BLR gas with an estimate of the size of the BLR based on time delay measurements (Peterson 1993). Reverberation mapping masses have been derived for about three dozen black holes (Wandel, Peterson & Malkan 1999; Kaspi et al. 2000). These masses fall a factor of 5-20 below the M - L_bulge relation defined by ground-based, stellar kinematical data (Wandel 1999, 2000).

• Quasar Light vs. Black Hole Demographics. The mass density of black holes at large redshifts can be estimated by requiring the optical QSO luminosity function to be reproduced by accretion onto black holes (Soltan 1982). Assuming a standard accretion efficiency of ~ 10%, the mean mass density in black holes works out to be ~ 2 × 10⁵ M Mpc^-3 (Chokshi & Turner 1992; Salucci et al. 1999). A similar argument based on the X-ray background gives consistent results, ~ 3 × 10⁵ M Mpc^-3 (Fabian & Iwasawa 1999; Salucci et al. 1999). By comparison, the black hole mass density implied by stellar kinematical modelling was about ten times higher (Magorrian et al. 1998; Richstone et al. 1998; Faber 1999).

Serious inconsistencies like these only appeared when comparisons were made with black hole masses derived from the stellar kinematical data; all other techniques gave roughly consistent values for and <M / M_bulge>. Nevertheless, most authors accepted the correctness of the stellar dynamical mass estimates and looked elsewhere to explain the discrepancies. Ho (1999) suggested that the reverberation mapping masses had been systematically underestimated. Wandel (1999) proposed that black holes in active galaxies were smaller on average than those in quiescent galaxies, due either to different accretion histories or to selection effects. Richstone et al. (1998) and Faber (1999) suggested that the inconsistency between their group's masses and the masses inferred from quasar light could be explained if black holes had acquired 80% of their mass after the quasar epoch through some process that produced no observable radiation.

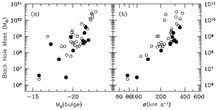
Figure 1. Discovery of the M - relation (adapted from Ferrarese & Merritt 2000). (a) M vs. bulge luminosity; (b) M vs. bulge velocity dispersion. "Sample A" masses, derived from high quality data, are indicated with filled circles; "Sample B" masses, from lower quality data, are the open circles.

What particularly caught our attention was the gulf between black hole masses derived from high- and low-resolution data, and (to a lesser extent) between gas- and stellar dynamical data; the former (e.g. Ferrarese, Ford & Jaffe 1996; Ferrarese & Ford 1999) were typically taken at higher resolution than the latter. Black hole masses derived from the highest resolution data, in galaxies like the Milky Way (Ghez et al. 1998; Genzel et al. 2000) and M87 (Macchetto et al. 1997), were the smallest when expressed as a fraction of the bulge mass, with M / M_bulge 10^-3. The largest fractional black hole masses - in galaxies like NGC 3377 (Kormendy et al. 1998) or NGC 4486b (Kormendy et al. 1997) - were mostly derived from stellar absorption-line spectra obtained from the ground, at resolutions of ~ 1", corresponding to typical linear scales of 10 - 100 pc. The mean value of M / M_bulge for these galaxies was claimed to be about 10^-2 (Magorrian et al. 1998; Richstone et al. 1998), roughly an order of magnitude greater than the value derived from the high-resolution data. We began to suspect that some of the masses derived from the lower-quality data might be serious over-estimates - or, even worse, that some of the "detections" based on these data were spurious.

To test this hypothesis, we tabulated all of the published black hole masses that had been derived from stellar- or gas kinematical data (excluding the reverberation mapping masses) and divided them into two groups based on their expected accuracy. This is not quite as easy as it sounds, since the "accuracy" of a black hole mass estimate is not necessarily related in any simple way to its published confidence range. Our criterion was simply the quality of the data: "accurate" black hole masses were those derived from HST data, at resolutions of ~ 0.1", as well as M for the Milky Way black hole (which is by far the nearest) and the black hole in NGC 4258 (for which VLBI gives a resolution of ~ 0.1 pc). The velocity data for these galaxies (our "Sample A") was always found to exhibit a clear rise in the inner few data points, suggesting that the black hole's sphere of influence r_h GM / ² had been well resolved. The remaining black hole masses ("Sample B") were all those derived from lower-resolution data, typically ground-based stellar kinematics, including most of the masses in the Magorrian et al. (1998) study. Sample A contained 12 galaxies, Sample B 31.

Our first attempt to compare "Sample A" and "Sample B" masses was disappointing (Figure 1a). In the M - L_bulge plane, the Sample A masses do fall slightly below those from Sample B, but the intrinsic scatter in L_bulge is apparently so large that there is no clear difference in the relations defined by the two samples.

But when we plotted M versus the velocity dispersion of the bulge stars, something magical happened (Figure 1b): now the Sample A galaxies clearly defined the lower edge of the relation, while the Sample B galaxies scattered above, some by as much as two orders of magnitude in M! Furthermore the correlation defined by the Sample A galaxies alone was very tight.

What particularly impressed us about the M - plot was the fact that the Sample A galaxies, which are diverse in their properties, showed such a tight correlation; while the Sample B galaxies, which are much more homogeneous, exhibited a large scatter. For instance, Sample A contains two spiral galaxies, two lenticulars, and both dwarf and giant ellipticals; while the Sample B galaxies are almost exclusively giant ellipticals. Furthermore the black hole masses in Sample A were derived using a variety of techniques, including absorption-line stellar kinematics (M32, NGC 4342), dynamics of gas disks (M87, NGC 4261), and velocities of discrete objects (MW, NGC 4258); while in Sample B all of the black hole masses were derived from stellar spectra obtained from the ground. This was circumstantial, but to us compelling, evidence that the Sample A masses were defining the true relation and that the Sample B masses were systematically in error.

Fitting a regression line to logM vs. log for the Sample A galaxies alone, we found

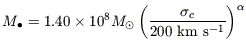
(1)

with = 4.80 ± 0.5 (Ferrarese & Merritt 2000). We defined the quantity _c to be the rms velocity of stars in an aperture of radius r_e/8 centered on the nucleus, with r_e the half-light radius of the bulge. This radius is large enough that the stellar velocities are expected to be affected at only the few percent level by the gravitational force from the black hole, but small enough that _c can easily be measured from the ground.

A striking feature of the M - relation is its negligible scatter. The reduced ² of Sample A about the best-fit line of Eq. 1, taking into account measurement errors in both variables, is only 0.74, essentially a perfect fit. Such a tight correlation seemed almost too good to be true (and may in fact be a fluke resulting from the small sample size) but we felt we could not rule it out given the existence of other, similarly tight correlations in astronomy, e.g. the near-zero thickness of the elliptical galaxy fundamental plane.

Figure 2. Detectability of black holes in galaxies for which dynamical mass determinations have been published or are planned. Horizontal axis is rh GM / 2, the black hole's radius of influence. M is computed from the M - relation for all forthcoming and ground-based observations. Vertical axis is the ratio of the observational resolution to twice rh. Determination of M is difficult when this ratio is 1, and mass determinations based on stellar dynamics (red symbols) can be difficult even when FWHM / 2rh < 1, for reasons discussed in the text.

In fact the scatter in the M - relation is so small that it is reasonable to use the relation to predict black hole masses, even in galaxies for which determinations of M based on detailed modelling have previously been published. One can then ask, galaxy by galaxy, whether the observations on which the published estimate of M was based were of sufficiently high quality to resolve the black hole's sphere of influence. Table 1 and Figure 2 show the results. Table 1 is a ranked list of the most secure black hole detections to date. The galaxies are listed in order of increasing FWHM / 2r_h, i.e. the ratio of the size of the resolution element to twice the radius of influence of the black hole. In the case of HST observations, for which the PSF is undersampled, FWHM is the diameter of the FOS aperture or the width of the STIS slit. For ground-based observations, FWHM refers to the seeing disk. Figure 2 plots the same quantities for essentially all galaxies with published estimates of M based on stellar or gas kinematics.

Not surprisingly, only the black holes in the Milky Way and in NGC 4258 have been observed at a resolution greatly exceeding r_h. The Sample A galaxies of Ferrarese & Merritt (2000) also satisfy FWHM / 2r_h < 1, although sometimes marginally. By contrast, almost none of the ground-based data resolved r_h, sometimes failing by more than a factor of 10.

Table 1. Ranked Census of Supermassive Black Hole Detections ^1,2

Galaxy	Type	Distance	M	c	FWHM/2rh	Reference
Galaxies for which rh has been resolved
MW	SbI-II	0.008	0.0295±0.0035	100±20	7.3-4	Genzel et al. 2000
N4258	SAB(s)bc	7.2	0.390±0.034	138±18	1.1-3	Miyoshi et al. 1995
N4486	E0pec	16.7	35.7±10.2	345±45	0.03	Macchetto et al. 1997
N3115	S0-	9.8	9.2±3.0	278±36	0.04	Emsellem et al. 1999
N221	cE2	0.8	0.039±0.009	76±10	0.06	Joseph et al. 2000
N5128	S0pec	4.2	2.4 3.6-1.7	145±25	0.10	Marconi et al. 2001
N4374	E1	18.7	17 +12-6.7	286±37	0.10	Bower et al. 1998
N4697	E6	11.9	1.7 +0.2-0.3	163±21	0.10	"Nuker" group, unpubl.3
N4649	E2	17.3	20.6 +5.2-10.2	331±43	0.10	"Nuker" group, unpubl.3
N4261	E2	33.0	5.4 +1.2-1.2	290±38	0.18	Ferrarese et al. 1996
M81	SA(s)ab	3.9	0.68 0.07-0.13	174±17	0.19	STIS IDT, unpubl.3
N4564	E	14.9	0.57 +0.13-0.17	153±20	0.33	"Nuker" group, unpubl.3
I1459	E3	30.3	4.6±2.8	312±41	0.35	Verdoes Kleijn et al. 2000
N5845	E*	28.5	2.9 +1.7-2.7	275±36	0.40	"Nuker" group, unpubl.3
N3379	E1	10.8	1.35±0.73	201±26	0.44	Gebhardt et al. 2000a
N3245	SB(s)b	20.9	2.1±0.5	211±19	0.48	Barth et al. 2001
N4342	S0-	16.7	3.3 +1.9-1.1	261±34	0.56	Cretton & van den Bosch 1999
N7052	E	66.1	3.7 +2.6-1.5	261±34	0.66	van der Marel & van den Bosch 1998
N4473	E5	16.1	0.8 +1.0-0.4	188±25	0.77	"Nuker" group, unpubl.3
N6251	E	104	5.9±2.0	297±39	0.84	Ferrarese & Ford 1999
N2787	SB(r)0+	7.5	0.41 0.04-0.05	210±23	0.87	Sarzi et al. 2001
N3608	E2	23.6	1.1 +1.4-0.3	206±27	0.98	"Nuker" group, unpubl.3
Galaxies for which rh has not been resolved
N3384	SB(s)0-	11.9	0.14 +0.05-0.04	151±20	1.0	"Nuker" group, unpubl.3
N4742	E4	15.5	0.14 0.04-0.05	93±10	1.0	STIS IDT, unpubl.3
N1023	S0	10.7	0.44±0.06	201±14	1.1	STIS IDT, unpubl.3
N4291	E	26.9	1.9 +1.3-1.1	269±35	1.1	"Nuker" group, unpubl.3
N7457	SA(rs)0-	13.5	0.036 +0.009-0.011	73±10	1.1	"Nuker" group, unpubl.3
N821	E6	24.7	0.39 +0.17-0.15	196±26	1.3	"Nuker" group, unpubl.3
N3377	E5+	11.6	1.10 +1.4-0.5	131±17	1.3	"Nuker" group, unpubl.3
N2778	E	23.3	0.13 +0.16-0.08	171±22	2.8	"Nuker" group, unpubl.3
Galaxies in which dynamical studies are inconclusive
N224	Double nucleus, system not in dynamical equilibrium.					Bacon et al. 2001
N598	Data imply upper limit only, 103 M.					Merritt, Ferrarese & Joseph 2001
N1068	Velocity curve is sub-Keplerian.					Greenhill et al. 1996
N3079	Masers do not trace a clear rotation curve.					Trotter et al. 1998
N4459	Data do not allow unconstrained fits.					Sarzi et al. 2001
N4486B	Double nucleus, system not in dynamical equilibrium.					STIS IDT, unpubl.2
N4945	Asymmetric velocity curve; velocity is sub-Keplerian.					Greenhill et al. 1997
1 Type is revised Hubble type. Black hole masses are in 108 solar masses, velocity dispersions are in km s-1, and distances are in Mpc. c is the aperture-corrected velocity dispersion defined by Ferrarese & Merritt (2000). rh = GM / c2, with M the value in column 4. References in column 7 are to the papers in which the dynamical analysis leading to the mass estimate were published.
2 For the reasons outlined in the text, the masses from Magorrian et al. (1998) are omitted from this tabulation. This includes NGC 4594, which was included in Kormendy & Gebhardt (2001).
3 Preliminary masses tabulated in Kormendy & Gebhardt (2001). Data and modelling for these mass estimates are not yet available.

The latter point is important, since precisely these data were used to define the canonical relation between black hole mass and bulge luminosity (Magorrian et al. 1998; Richstone et al. 1998; Faber 1999) that has served as the basis for so many subsequent studies (e.g. Haehnelt, Natarajan & Rees 1998; Catteneo, Haehnelt & Rees 1999; Salucci et al. 1999; Kauffmann & Haehnelt 2000; Merrifield, Forbes & Terlevich 2000). Figure 3 plots the likely "error" in the ground-based mass estimates (defined as the ratio of the quoted mass, M_fit, to the mass implied by Eq. 1) as a function of the effective resolution FWHM / 2r_h. The error is found to correlate strongly with the quality of the data. For the best-resolved of the Magorrian et al. candidates, FWHM/2r_h 1, the average error in M appears to be a factor of ~ 3, rising roughly linearly with FWHM/r_h to values of ~ 10² for the most poorly-resolved candidates.

Figure 3. "Error" in published black hole masses, defined as the ratio of the published mass estimate Mfit to the value M inferred from the M - relation, as a function of the effective resolution of the data from which the mass estimate was derived. The error increases roughly inversely with resolution for FWHM / 2rh 1. Most of the ground-based detections are in this regime.

An important quantity is the mean ratio of black hole mass to bulge mass, <M / M_bulge>. Figure 4 compares the distribution of M_fit/M_bulge, the mass ratio computed by Magorrian et al. (1998), to the distribution obtained when M_fit is replaced by M as computed from the M - relation. The mean value of (M / M_bulge) drops from 1.7 × 10^-2 to 2.5 × 10^-3, roughly an order of magnitude. The mean value of log₁₀(M / M_bulge) shifts downward by -0.7 corresponding to a factor ~ 5 in M / M_bulge. The density of black holes in the local universe implied by the lower value of <M / M_bulge> is ~ 5 × 10⁵ M Mpc^-3 (Merritt & Ferrarese 2001a), consistent with the value required to explain quasar luminosities assuming a standard accretion efficiency of 10% (Chokshi & Turner 1992; Salucci et al. 1999; Barger et al. 2001).

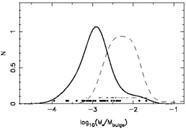
Figure 4. Frequency function of black-hole-to-bulge mass ratios (adapted from Merritt & Ferrarese 2001a). The dashed curve is the "Magorrian relation" (Magorrian et al. 1998) based on black hole masses derived from ground-based kinematics and two-integral modelling. The solid curve is the frequency function obtained when black hole masses are instead computed from the M - relation.

2.2. Pitfalls of Stellar Dynamical Mass Estimation

Why were most of the stellar dynamical mass estimates so poor; why were they almost always over-estimates; and what lessons do past mistakes have for the future? The answer to the first question is simple in retrospect. Figure 5 shows how the signal of the black hole - a sudden rise in the rms stellar velocities at a distance of ~ r_h GM / ² from the black hole - is degraded by seeing. For FWHM/2r_h 2, the signal is so small as to be almost unrecoverable except with data of exceedingly high S/N. Most of the ground-based observations fall into this regime (Figure 2). In fact the situation is even worse than Figure 5 suggests, since for FWHM r_h, the rise in (R) will be measured by only a single data point. This is the case for many of the galaxies that are listed as "resolved" in Table 1 (e.g. NGC 3379, Gebhardt et al. 2000a).

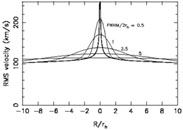
Figure 5. Degradation due to seeing of the velocity dispersion spike produced by a black hole in a hot (nonrotating) stellar system. Heavy line is the profile unaffected by seeing; R is the projected distance from the black hole and rh = GM / 2. When FWHM / 2rh ~ 2, the velocity dispersion spike is so degraded as to be almost unrecoverable. Most ground-based observations fall into this regime (Fig. 2).

A short digression is in order at this point. Data taken from the ground often show an impressive central spike in the velocity dispersion profile; examples are NGC 4594 (Kormendy et al. 1996b) and NGC 4486b (Kormendy et al. 1997). However such features are due in part to blending of light from two sides of the nucleus where the rotational velocity has opposite signs and would be almost as impressive even if the black hole were not present. This point was first emphasized by Tonry (1984) in the context of his ground-based M32 observations. As he showed, the velocity dispersion spike in M32 as observed at ~ 1" resolution is consistent with rotational broadening and does not require any increase in the intrinsic velocity dispersion near the center.

Why should poor data lead preferentially to overestimates of M, rather than random errors? There are two reasons. First, as pointed out by van der Marel (1997), much of the model-fitting prior to 1999 was carried out using isotropic spherical models or their axisymmetric analogs, the so-called "two-integral" (2I) models. Such models predict a velocity dispersion profile that gently falls as one moves inward, for two reasons: non-isothermal cores, i.e. ~ r^- with {0, 2}, generically have central minima in the rms velocity (e.g. Dehnen 1993); and, when flattened, the 2I axisymmetric models become dominated by nearly circular orbits (in order to maintain isotropy in the meridional plane) further reducing the predicted velocities near the center. Figure 6 illustrates these effects for a set of axisymmetric 2I models with = 1.5. Real galaxies almost always exhibit a monotonic rise in v_rms. Adding a central point mass can correct this deficiency of the models, but only an unphysically large value of M_fit will affect the stellar motions at large enough radii, r 0.1 r_e, to do the trick. This is probably the explanation for the factor ~ 3 mean error in M derived from the best ground-based data (Figure 3).

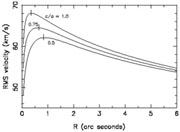
Figure 6. Velocity dispersion profiles of the "two-integral" (2I) models that were used as templates for estimating black hole masses in many of the stellar kinematical studies (e.g. Magorrian et al. 1998). Model flattening is indicated as c/a; there are no central black holes. Ticks mark the point Rmax of maximum velocity; Rmax moves outward as the flattening is increased.

The much larger values of M_fit / M associated with the more distant galaxies in Figure 3 are probably attributable to a different factor. When the data contain no useful information about the black hole mass, only values of M_fit that are much larger than the true mass will significantly affect the ² of the model fits. The only black holes that can be "seen" in such data are excessively massive ones.

Can these problems be overcome by abandoning 2I models in favor of more general, three-integral (3I) models? The answer, surprisingly, is "no": making the modelling algorithm more flexible (without also increasing the amount or quality of the data) has the effect of weakening the constraints on M. The reason is illustrated in Figure 7. The rms velocities in 2I models are uniquely determined by the assumed potential, i.e. by M_fit and M/L, the mass-to-light ratio assumed for the stars. This means that the models are highly over-constrained by the data - there are far more observational constraints (velocities) than adjustable parameters (M_fit, M/L), hence one expects to find a unique set of values for M_fit and M/L that come closest to reproducing the data. This is the usual case in problems of statistical estimation and it implies a well-behaved set of ² contours with a unique minimum.

When the same data are modeled using the more general distribution of orbits available in a 3I model, the problem becomes under-constrained: now one has the freedom to adjust the phase-space distribution function in order to compensate for changes in M_fit and M/L, so as to leave the goodness of fit precisely unchanged. The result is a plateau in ² (Figure 7), the width of which depends in a complicated way on the ratio of observational constraints to number of orbits or phase-space cells in the modelling algorithm (Merritt 1994). Thus, 3I modelling of the ground-based data would only show that the range of possible values of M_fit includes, but is not limited to, the values found using the 2I models; it would not generate more precise estimates of M unless the data quality were also increased.

Figure 7. Schematic comparison of two-integral (2I) and three-integral (3I) modelling of stellar kinematical data; Mfit is the estimated black hole mass. 2I models predict a unique rms velocity field given an assumed mass distribution; in 3I models, the extra freedom associated with a more general distribution of orbits allows one to compensate for changes in Mfit in such a way as to leave the goodness of fit to the data precisely unchanged.

The greater difficulty of interpreting results from 3I modelling has not been widely appreciated; few authors make a distinction between "indeterminacy" in M (the width of the constant-² plateau in Figure 7) and "uncertainty" (the additional range in M allowed by measurement errors), or look carefully at how their confidence range depends on the number of orbits used. We illustrate these difficulties by examining two recently published studies based on high quality, stellar kinematical data.

1. NGC 3379 (Gebhardt et al. 2000a): The prima-facie evidence for a central mass concentration in this galaxy consists of a single data point, the innermost velocity dispersion as measured by HST/FOS; the rotation curve exhibits no central rise, in fact it drops monotonically toward the center. Goodness-of-fit contours generated from 3I models show the expected plateau (Fig. 7 of Gebhardt et al.), extending from ~ 10⁶ M to ~ 3 × 10⁸ M. In fact a model with M = 0 fits the data just as well: the authors state that "the difference between the no-black hole and black hole models is so subtle" as to be almost indiscernable (cf. their Fig. 11). Gebhardt et al. nevertheless argue for M > 0 based on the poorly-determined wings of stellar velocity distribution measured within the central FOS resolution element. In view of the fact that this velocity distribution exhibits a puzzling unexplained asymmetry (their Fig. 4), the stellar dynamical case for a black hole in this galaxy should probably be considered marginal.

2. NGC 4342 (Cretton and van den Bosch 1999): The evidence for a central mass concentration is again limited to a single data point, the central FOS velocity dispersion. Cretton & van den Bosch find that a black-hole-free model provides "fits to the actual data [that] look almost indistinguishable from that of Model B" (a model with M_fit = 3.6 × 10⁸ M). Their ² contours (their Fig. 7) nevertheless seem to show a preferred black hole mass; however they note that ² is dominated by the data at radii R 5", far outside of the radius of influence of the black hole. The probable culprit here is the modest number of orbits (1400, compared with ~ 250 constraints) in their 3I solutions. Outer data points are always the most difficult to fit when modelling via a finite orbit library since only a fraction of the orbits extend to large radii; this is clear in their fits (cf. their Fig. 8) which become progessively worse at large radii.

We emphasize that both of these modelling studies were based on high-quality data, with FWHM / 2r_h 0.4 (NGC 3379) and 0.6 (NGC 4342) (Table 1). Nevertheless, the extreme freedom associated with 3I models permits a wide range of black hole masses to be fit to the velocity data in both galaxies. As Figure 2 shows, most of the galaxies in the ongoing HST/STIS survey of galactic nuclei will be observed at even lower effective resolutions; hence we predict that the black hole masses in many of these galaxies will turn out to be consistent with zero and that the range of allowed masses will usually be large. (To be fair, we note that these observations were planned at a time when <M / M_bulge> was believed to be much larger than it is now.) We therefore urge caution when interpreting results like Kormendy & Gebhardt's (2001) recent compilation of black hole masses derived from unpublished 3I modelling.