4. ABUNDANCES AT HIGH RED-SHIFT

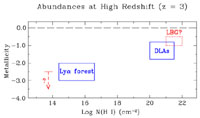
Figure 6. Summary of our current knowledge of abundances at high red-shift. Metallicity is on a log scale relative to solar and N(H I) is the column density of neutral hydrogen measured in the Lyman- forest, damped Lyman- systems and Lyman break galaxies, after Pettini (1999). Courtesy Max Pettini.

Naturally recent advances in studies of objects at high red-shift supply vital clues to the early evolution of galaxies, but, as Pettini (1999) has emphasised, our knowledge in this area is severely limited (see Figure 6), giving rise to serious observational selection effects. The Lyman forest comes from condensations in the intergalactic medium, possibly analogues of the high-velocity H I clouds seen today (Blitz et al. 1999), and represents the majority of the baryonic matter in the universe, while the damped Lyman- (DLA) systems have a co-moving density similar to that of disk galaxies today. Then there are also the Lyman break galaxies, for which there is some information based on the strength of their stellar winds. Figure 7 shows the metallicities of DLA systems, based on zinc abundance, plotted against red-shift, after Pettini (1999). When column-density weighted means are formed in distinct red-shift bins, no evolution is detectable in the metallicity and there is no obvious way of identifying what sort of objects these systems will eventually become. Some clues could come from element:element ratios like N/O or /Fe. Here the difficulty lies in correcting for depletion from the gas phase on to dust, which can be estimated (when not too large) from the ratio of Zn to Cr and Fe, since their intrinsic relative abundances are usually constant. According to Vladilo (1998) and Pettini et al. (1999a, b), the resulting relative abundances of silicon and iron are pretty much solar (or like the Magellanic Clouds and the "anomalous" halo stars referred to above), suggesting that they are destined to become Im galaxies rather than large spirals. The behaviour of N/Si vs Si/H also shows a resemblance to the behaviour of N/O vs. O/H in irregular and blue compact galaxies with perhaps an even greater scatter around the normal primary-secondary pattern than is found in irregulars and BCGs (Lu, Sargent & Barlow 1998).

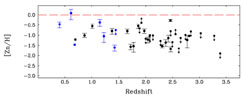
Figure 7. Zn abundance against red-shift for 40 DLAs from Pettini et al. (1999). Courtesy Max Pettini.

What are the consequences of the new star formation rate density (Fig 1) for "metal" production and global chemical evolution? To begin with, the SFR which I shall call _*(conv.) is based on the rest-frame UV luminosity density combined with a Salpeter power-law IMF between 0.1 and 100 M. The co-moving metal production-rate density is then usually deduced by dividing by the magic number of 42 (shades of The Hitch-Hiker's Guide to the Galaxy), which comes from models of supernova yields in the range of 10 to 100 M or so, and I shall call this metal production rate _Z(conv.). The overall yield then amounts to

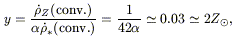
(3)

where 0.7 is the lock-up fraction. Such a high yield is excessive for the solar neighbourhood (although it may be suitable for intra-cluster gas) and so people modelling Galactic chemical evolution generally either use a steeper slope, a smaller lower mass limit or assume that stars above 40 or 50 M lock the bulk of their element production in black holes. So the true rate of "metal" production should be _Z(conv.), where 1 is some correction factor depending on your favourite model of galactic chemical evolution. Finally, the true star formation rate density should be corrected by some factor , also 1, for the undoubted flattening of the IMF power law somewhere below 1 M, e.g. Fukugita, Hogan & Peebles (1998) have = 0.65, but this does not influence the conversion factor (at least to first order) because it is mainly just the massive stars that produce both the metals and the UV luminosity.

With these preliminaries, we can use the data supplied by Pettini (1999) to draw up the following inventory of stars and metals for the present epoch and for a red-shift of 2.5, assuming = 0.67, = 0.65.

Table 1. Inventory of stars and metals at z = 0 and z = 2.5

	z = 0	z = 2.5
* = *(conv.) dt	3.6 × 108 M Mpc-3	9 × 107 M Mpc-3
* = * / 7.7 × 1010 h502	.0047h50-2	.0012h50-2
*(FHP 98)	.0049h50-1
Z = y * = * / (42 )	2.0 × 107 M Mpc-3	5 × 106 M Mpc-3
Z (predicted)	2.6 × 10-4 h50-2	6.5 × 10-5 h50-2
Z (stars, Z = Z)	1.0 × 10-4 h50-1
Z (hot gas, Z = 0.3Z)	1.7 × 10-4h50-1.5
	-> 0.4 1
Z (DLA, Z = 0.07Z)		3 × 10-6 h50-1
Z (Ly. forest, Z = 0.003Z)		4 × 10-6 h50-2
Z (Ly. break gals, Z = 0.3Z)		?
Z (hot gas)		?

Somewhat more troubling questions arise at red-shift 2.5, however, as Pettini (1999) has already pointed out. It now seems that about a quarter of the stars have already been formed by then (in ellipticals, bulges and thick disks?), but known entries in the table only account for 10 per cent of the resulting metals (if = 1) or 25 per cent (if = 0.4). This is a good measure of the incompleteness in our knowledge of the distribution of the elements at substantial red-shifts.

I thank Max Pettini for supplying data and for enlightening discussions.