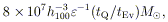Reprinted with kind permission from , 4139 El
Camino Way, Palo Alto, California, USA
BLACK HOLE MODELS FOR ACTIVE GALACTIC NUCLEI
Martin J. Rees
Institute of Astronomy, Madingley Road,
Cambridge CB3 0HA, England
Table of Contents
 INTRODUCTION
INTRODUCTION
 INFERENCES INSENSITIVE TO DETAILED MODEL
INFERENCES INSENSITIVE TO DETAILED MODEL
 Some Fiducial Numbers
Some Fiducial Numbers
 Processes in Ultrahot Thermal Plasma
Processes in Ultrahot Thermal Plasma
 Cyclotron/Synchrotron and Inverse Compton Cooling
Cyclotron/Synchrotron and Inverse Compton Cooling
 RADIAL ACCRETION FLOWS
RADIAL ACCRETION FLOWS
 Spherical Accretion
Spherical Accretion
 BLACK HOLES ACCORDING TO GENERAL RELATIVITY
BLACK HOLES ACCORDING TO GENERAL RELATIVITY
 The Kerr Metric
The Kerr Metric
 Three Astrophysically Important Relativistic
Effects
Three Astrophysically Important Relativistic
Effects
 ACCRETION FLOWS WITH ANGULAR MOMENTUM
ACCRETION FLOWS WITH ANGULAR MOMENTUM
 Origin of Infalling Matter
Origin of Infalling Matter
 Thin Disks
Thin Disks
 General Structure of Tori or Thick Disks
General Structure of Tori or Thick Disks
 RADIATION-SUPPORTED TORI
RADIATION-SUPPORTED TORI
 Ion-Supported Tori
Ion-Supported Tori
 JET FORMATION
JET FORMATION
 SOME COMMENTS ON PHENOMENOLOGY
SOME COMMENTS ON PHENOMENOLOGY
 The Continuum Spectrum
The Continuum Spectrum
 Ordinary QSOs
Ordinary QSOs
 Radio Galaxies
Radio Galaxies
 Radio Quasars and Optically Violent Variables
(OVVs)
Radio Quasars and Optically Violent Variables
(OVVs)
 Hard X-Ray and Gamma-Ray Sources
Hard X-Ray and Gamma-Ray Sources
 DEMOGRAPHY OF AGNs
DEMOGRAPHY OF AGNs
 SOME CONCLUDING COMMENTS
SOME CONCLUDING COMMENTS
 REFERENCES
REFERENCES
1. INTRODUCTION
It is now 20 years since active galactic nuclei (AGNs) became widely
acknowledged as an important astrophysical phenomenon
(33,
109). Over
the entire subsequent period, one of the few statements to command
general agreement has been that the power supply is primarily
gravitational: the whole bestiary of models involving dense star
clusters, supermassive stars, or black holes at least have this
feature in common. Systems dependent on gravitational energy have
something else in common: they all undergo an inexorable runaway as
the central potential well gets deeper and deeper. According to
conventional physics, the almost inevitable endpoint of any dense star
cluster or supermassive star will be the collapse of a large fraction
of its total mass to a black hole. This is the "bottom line" of
Figure 1. Such arguments suggest that massive
black holes should exist in the
nuclei of all galaxies that have ever experienced a violently active
phase. Furthermore, physical processes involving black holes offer a
more efficient power supply than any of the "precursor" objects
depicted in Figure 1. So massive black holes may
not merely be the
defunct remnants of violent activity; they may also participate in its
most spectacular manifestations.
Considerations such as these have shifted the emphasis of
theoretical work away from dense star clusters and supermassive stars
and have motivated fuller (or at least less perfunctory)
investigations of how black holes might generate the power in quasars,
radio galaxies, and related objects. All of the evolutionary tracks in
Figure 1 deserve more study: none can be
dismissed as irrelevant to
the AGN phenomenon. The present review is nevertheless focused on
black hole models. Moreover, its scope is even more restricted: I am
primarily concerned here with what goes on close to the black hole -
in the region where the gravitational potential is not merely "(1/r),"
but where intrinsically relativistic features can also be
significant. Although this is where the power output is concentrated,
many conspicuous manifestations of AGNs - the emission lines, the
radio components, etc. - involve some reprocessing of this energy on
larger scales. For this reason (and also because of space
limitations), little is said here about phenomenology: I merely
discuss some physical processes and simple idealized models that have
been advanced as ingredients of AGNs.

|
Figure 1. Schematic diagram [reproduced
from Rees (106)] showing
possible routes for runaway evolution in active galactic nuclei.
|
Two obvious generic features of active galactic nuclei are (a) the
production of continuum emission, which in some cases at least must be
nonthermal (probably synchrotron); and (b) the expulsion of energy in
two oppositely directed beams. The activity is manifested on many
scales - up to several megaparsecs in the case of the giant radio
sources. It is a tenable hypothesis, however - and one implicitly
adopted here - that the central prime mover is qualitatively similar
in all of the most highly active nuclei, and that the wide differences
observed reflect "environmental" factors on larger scales (where the
primary energy output can be reprocessed) and perhaps orientation
effects as well.
2. INFERENCES INSENSITIVE TO DETAILED MODEL
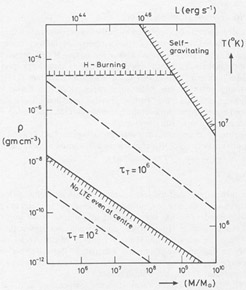
2.1 Some Fiducial Numbers
Before focusing on specific properties of black holes, it is
interesting to consider some general features of compact ultraluminous
sources. Certain order-of-magnitude quantities are involved in any
model.
A central mass M has a gravitational radius
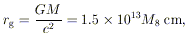
| (1)
|
where M8 is the mass in units of
108
M . The
characteristic minimum time scale for variability is
. The
characteristic minimum time scale for variability is
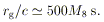
| (2)
|
A characteristic luminosity is the "Eddington limit," at which
radiation pressure on free electrons balances gravity:
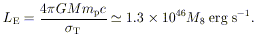
| (3)
|
Related to this is another time scale
(112):
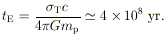
| (4)
|
This is the time it would take an object to radiate its entire
rest mass if its luminosity were LE. The characteristic
blackbody
temperature if luminosity LE is emitted from radius
rg is
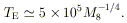
| (5)
|
We can further define a characteristic magnetic field, whose
energy density is comparable with that of the radiation. Its value is
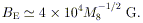
| (6)
|
The expected field strengths induced by accretion flows can be
of this order. The corresponding cyclotron frequency is
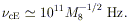
| (7)
|
The Compton cooling time scale for a relativistic electron of
Lorentz factor
 e (equivalent to
the synchrotron lifetime in the field BE) is
e (equivalent to
the synchrotron lifetime in the field BE) is
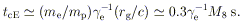
| (8)
|
The photon density
n within
the source volume is
~ (L/r2c) /
<h
within
the source volume is
~ (L/r2c) /
<h >. If a
luminosity
f LE emerges in photons with
h
>. If a
luminosity
f LE emerges in photons with
h
 me
c2, which can
interact (with a cross section
~
me
c2, which can
interact (with a cross section
~  T) to produce
electron-positron pairs
(40),
then these photons will interact before escaping if
T) to produce
electron-positron pairs
(40),
then these photons will interact before escaping if
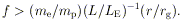
| (9)
|
Several inferences now follow about the radiation processes,
given
only the assumption that a primary flux with
L  LE is
generated within radii a few times rg:
LE is
generated within radii a few times rg:
- Thermal radiation from optically thick material would be in the
far-ultraviolet or soft X-ray region; if, however, thermal gas in the
region were hot enough to emit X-rays, reabsorption would be
unimportant.
- If the bulk of the luminosity L were synchrotron radiation in a
field
B
 BE (Equation 6), then the
self-absorption turnover would be
(99)
BE (Equation 6), then the
self-absorption turnover would be
(99)
| (10)
|
(i.e. typically in the infrared). No significant radio
emission can
come directly from
r  rg unless some coherent process operates at
rg unless some coherent process operates at


 cE. Synchrotron
emission at ~
cE. Synchrotron
emission at ~  sE would
require electrons with
sE would
require electrons with
 e
e
 40M81/14.
40M81/14.
- The synchrotron or inverse Compton lifetimes of relativistic
electrons is
<< (rg/c) under these conditions,
so in any model involving such
mechanisms, the radiating particles must be injected or repeatedly
reaccelerated at many sites distributed through the source volume.
- If a substantial fraction of the radiation were generated as gamma
rays with energies
 1 Mev, then
electron-positron pairs would inevitably be produced.
1 Mev, then
electron-positron pairs would inevitably be produced.
This last point is less familiar than the previous three, and so it
may merit some elaboration. Photons with energies above 0.5 Mev will
experience an optical depth to pair production that exceeds unity
whenever (Lf /r) exceeds a value equivalent to
~ 5 × 1029
erg s-1 cm-1.
Moreover, the annihilation rate constant for these pairs is
~  Tc if
they are subrelativistic, and smaller by
~
Tc if
they are subrelativistic, and smaller by
~  e2
if they are
ultrarelativistic (104).
This has the important consequence that a
compact source that produces gamma rays (either thermally or
nonthermally) at a steady rate satisfying
(9) will shroud itself
within an optically thick "false photosphere" of electron-positron
pairs, which scatters and Comptonizes all lower-energy photons
(58).
e2
if they are
ultrarelativistic (104).
This has the important consequence that a
compact source that produces gamma rays (either thermally or
nonthermally) at a steady rate satisfying
(9) will shroud itself
within an optically thick "false photosphere" of electron-positron
pairs, which scatters and Comptonizes all lower-energy photons
(58).
2.2. Processes in Ultrahot Thermal Plasma
The only quantities entering into the above discussion have been
essentially those involving the electromagnetic energy densities. We
now consider the physical conditions in plasma near a collapsed
object. If thermal plasma can radiate efficiently enough, it can cool
(even at
r  rg) to the relatively modest
temperature Te (Equation 5). However, two-body
cooling processes can be inefficient at low
densities; for this reason, and also because the energy available in
the relativistically deep potential well may amount to 100 Mev
ion-1,
the plasmas in AGNs may get hotter than those familiarly encountered
elsewhere (even by astrophysicists).
rg) to the relatively modest
temperature Te (Equation 5). However, two-body
cooling processes can be inefficient at low
densities; for this reason, and also because the energy available in
the relativistically deep potential well may amount to 100 Mev
ion-1,
the plasmas in AGNs may get hotter than those familiarly encountered
elsewhere (even by astrophysicists).
At ion temperatures up to, say,
kTi = 100 Mev the ions are of course
nonrelativistic, but the thermal electrons may be relativistic. The
main distinctive effects arise because the time scale for establishing
electron-ion equipartition via two-body processes, or even for setting
up a Maxwellian distribution among the electrons themselves, may
exceed the time scale for radiative cooling via the same two-body
effects. Moreover, other cooling processes may hold the electron
temperature to
 1 Mev even if the
ions are much hotter. Detailed
discussions of these various time scales are given by Gould
(54 -
56)
and Stepney (121).
1 Mev even if the
ions are much hotter. Detailed
discussions of these various time scales are given by Gould
(54 -
56)
and Stepney (121).
COMPTONIZATION If photons of energy hv are scattered by
electrons with temperature
Te such that
kTe >>
h , then there is a systematic
mean gain (67,
125)
in photon energy of
(
, then there is a systematic
mean gain (67,
125)
in photon energy of
(
 /
/
 )
)
 (kTe/mec2) until,
after many scatterings,
a Wien law is established. If soft photons are injected in an
optically thick
(
(kTe/mec2) until,
after many scatterings,
a Wien law is established. If soft photons are injected in an
optically thick
( T > 1) source,
then the emergent spectrum depends
essentially on the parameter
y =
T > 1) source,
then the emergent spectrum depends
essentially on the parameter
y =  T2(kTe /
mec2) : if y << 1,
nothing much
happens; if y >> 1, a Wien law is set up; but in the
intermediate case when
y
T2(kTe /
mec2) : if y << 1,
nothing much
happens; if y >> 1, a Wien law is set up; but in the
intermediate case when
y  1, the emergent
spectrum has an approximate power-law
form. When
kT
1, the emergent
spectrum has an approximate power-law
form. When
kT  me c2, the energy change in each
scattering is too
large for a diffusion approximation to be valid, and Monte Carlo
methods are needed (57).
me c2, the energy change in each
scattering is too
large for a diffusion approximation to be valid, and Monte Carlo
methods are needed (57).
Table 1. Main production/anihilation processes
for electron energies > 0.5 Mev
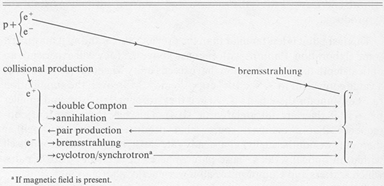
|
PAIR PRODUCTION EFFECTS When the electron energies on the
tail of the Maxwellian
distribution exceed a threshold of 0.5 Mev, collisional processes can
create not only gamma rays but also e+e-
pairs. These pairs then
themselves contribute to the cooling and opacity; the physical
conditions must therefore be computed self-consistently, with pairs
taken into account (22).
Discussions have been given by several
authors (22,
40,
69,
70,
132).
The main production/annihilation processes are summarized in
Table 1. Further high-energy processes can
operate above 50 Mev (46).
The fullest discussions of thermal balance in relativistic plasma that
take pairs into account are due to Lightman and collaborators
(7,
69,
70)
and Svensson (122 -
124).
There is a maximum possible equilibrium
temperature, of order 10 Mev; but if the heat input is raised beyond a
certain value, the increment in pair density is so great that the
temperature falls again toward 1 Mev. Note that to extend the usual
cooling function
 (Te)
into the temperature range where pair
production is important, one must specify the column density
nir of
the source as a second parameter (ni being the ion
density). When
nir << 1, the dominant pair production is via
e-p collisions; but for
sources of higher column density, relation (9) may be fulfilled, and
more pairs come from
(Te)
into the temperature range where pair
production is important, one must specify the column density
nir of
the source as a second parameter (ni being the ion
density). When
nir << 1, the dominant pair production is via
e-p collisions; but for
sources of higher column density, relation (9) may be fulfilled, and
more pairs come from
 +
+
 encounters.
encounters.
2.3. Cyclotron/Synchrotron and Inverse Compton
Cooling
Suppose that the magnetic energy is q times the rest mass density of
the plasma: we might expect
q  kTi / mp c2 for
accretion flows. The
ratio of the cyclotron cooling time (neglecting reabsorption) to the
bremsstrahlung time for a subrelativistic electron is
kTi / mp c2 for
accretion flows. The
ratio of the cyclotron cooling time (neglecting reabsorption) to the
bremsstrahlung time for a subrelativistic electron is
 f(me /
mp) q-1(kTe /
me c2)-1/2,
which is << 1 for a plasma with
kTi
f(me /
mp) q-1(kTe /
me c2)-1/2,
which is << 1 for a plasma with
kTi  1 Mev with an
equipartition field; for ultrarelativistic electrons the dominance of
synchrotron losses over bremsstrahlung is even greater. Analogously,
Compton losses can be very important: indeed, in any source where
Thomson scattering on electrons (or positrons) yields
1 Mev with an
equipartition field; for ultrarelativistic electrons the dominance of
synchrotron losses over bremsstrahlung is even greater. Analogously,
Compton losses can be very important: indeed, in any source where
Thomson scattering on electrons (or positrons) yields
 T > 1, the
requirement that the Compton
T > 1, the
requirement that the Compton
 -parameter be
-parameter be
 1 implies that the
electrons or positrons must be mostly subrelativistic.
1 implies that the
electrons or positrons must be mostly subrelativistic.
The conventional distinction between thermal and nonthermal
particles becomes somewhat blurred in these contexts where two-body
coupling processes cannot necessarily maintain a Maxwellian
distribution. Various acceleration mechanisms (relativistic shocks,
reconnection, etc.) may, moreover, boost some small fraction of the
particles to high  : such
mechanisms operate in many contexts in
high-energy astrophysics and should be even more efficient in an
environment where the bulk velocities and Alfvén speeds are both ~
c. These particles would then emit synchrotron or inverse Compton
radiation. Such acceleration would be "impulsive," in the sense that
its time scale is
<< rg / c. The accelerating force would be
eE, where
E(
: such
mechanisms operate in many contexts in
high-energy astrophysics and should be even more efficient in an
environment where the bulk velocities and Alfvén speeds are both ~
c. These particles would then emit synchrotron or inverse Compton
radiation. Such acceleration would be "impulsive," in the sense that
its time scale is
<< rg / c. The accelerating force would be
eE, where
E( B)
is the electric field "felt" by the charge. There is then a
characteristic peak energy attainable by such processes
(39), namely
that for which the radiative drag due to synchrotron and inverse
Compton emission equals eB. For
B = BE (Equation 6), this yields
B)
is the electric field "felt" by the charge. There is then a
characteristic peak energy attainable by such processes
(39), namely
that for which the radiative drag due to synchrotron and inverse
Compton emission equals eB. For
B = BE (Equation 6), this yields
 drag = 4 ×
105 M81/4.
For acceleration along straight field lines,
synchrotron losses are evaded, and the terminal energy could be
~ BErg (corresponding to
drag = 4 ×
105 M81/4.
For acceleration along straight field lines,
synchrotron losses are evaded, and the terminal energy could be
~ BErg (corresponding to
 e = 3 ×
1014M81/2) if
linear acceleration operated
over the whole scale of the source. Such limiting energies have
emerged from specific studies of accretion disk electrodynamics
(34,
72).
However, inverse Compton losses cannot be evaded in this way, and
they would set a limit not much greater than
e = 3 ×
1014M81/2) if
linear acceleration operated
over the whole scale of the source. Such limiting energies have
emerged from specific studies of accretion disk electrodynamics
(34,
72).
However, inverse Compton losses cannot be evaded in this way, and
they would set a limit not much greater than
 drag. (Individual ions,
not subject to radiative losses, could in principle get more energetic
than electrons.) The parameter
drag. (Individual ions,
not subject to radiative losses, could in principle get more energetic
than electrons.) The parameter
 drag scales as
B-1/2,
and electrons with this
energy emit synchrotron photons with
h
drag scales as
B-1/2,
and electrons with this
energy emit synchrotron photons with
h

 f-1
me c2 (i.e. 60 Mev)
(58,
99).
Inverse Compton radiation from the same electrons could of course
have photon energies right up to
f-1
me c2 (i.e. 60 Mev)
(58,
99).
Inverse Compton radiation from the same electrons could of course
have photon energies right up to
 drag
me c2. There is thus no
reason
why a (power-law?) spectrum should not extend up to the gamma-ray band.
drag
me c2. There is thus no
reason
why a (power-law?) spectrum should not extend up to the gamma-ray band.
3. RADIAL ACCRETION FLOWS
The plasma around black holes will be in some dynamical state -
participating in an accretion flow, or perhaps in a wind or jet.
Realistically, it would probably be very inhomogeneous: a "snapshot"
might reveal many dense filaments at T
 TE,
embedded in ultrahot
thermal plasma filling most of the volume, as well as localized sites
where ultrarelativistic electrons are being accelerated. But it is a
basic prerequisite for modeling to know how the various cooling and
microphysical time scales compare with the dynamical time at a radius
r (
TE,
embedded in ultrahot
thermal plasma filling most of the volume, as well as localized sites
where ultrarelativistic electrons are being accelerated. But it is a
basic prerequisite for modeling to know how the various cooling and
microphysical time scales compare with the dynamical time at a radius
r ( rg). The latter can written as
rg). The latter can written as
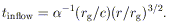
| (11)
|
The parameter  , equal to one
for free-fall, is introduced explicitly
at this stage because the numbers all scale straightforwardly to cases
(with
, equal to one
for free-fall, is introduced explicitly
at this stage because the numbers all scale straightforwardly to cases
(with
 < 1) where the inflow is
impeded by rotation or by pressure
gradients. (In deriving these characteristic numbers, we approximate
the flow as spherically symmetric: although this is roughly true for
thick tori, further geometrical factors obviously enter for thin
disks.)
< 1) where the inflow is
impeded by rotation or by pressure
gradients. (In deriving these characteristic numbers, we approximate
the flow as spherically symmetric: although this is roughly true for
thick tori, further geometrical factors obviously enter for thin
disks.)
If accretion with efficiency
 provides the power, the
value of
provides the power, the
value of  needed to supply a luminosity L can be written as
needed to supply a luminosity L can be written as

 E = (L /
LE)
E = (L /
LE)
 -1,
where
-1,
where  E =
LE /
c2. The particle density at
radius r corresponding to an inflow rate
E =
LE /
c2. The particle density at
radius r corresponding to an inflow rate
 is
is
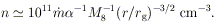
| (12)
|
Another quantity of interest is the Thomson optical depth at
radius r, which is
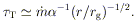
| (13)
|
The "trapping radius," within which an accretion flow would advect
photons inward faster than they could diffuse outward [i.e. within
which
 T > (c /
vinflow)] is
T > (c /
vinflow)] is
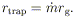
| (14)
|
Note that this depends only on
 and not on
and not on
 .
.
In Figure 2 are shown the ratios of various
physically important time scales to
tinflow for a radial free-fall with
 = 1, calculated on
the assumption that the ions at each radius are at the virial
temperature [i.e.
kTi = mp c2
(r / rg)-1]. This assumption is
self-consistent because bremsstrahlung cooling and electron-ion
coupling are indeed ineffective for
= 1, calculated on
the assumption that the ions at each radius are at the virial
temperature [i.e.
kTi = mp c2
(r / rg)-1]. This assumption is
self-consistent because bremsstrahlung cooling and electron-ion
coupling are indeed ineffective for

 = 1. If the
magnetic field is
close to equipartition, synchrotron cooling is effective for the
electrons (except insofar as it is inhibited by self-absorption);
Comptonization is important whenever
(k Te / me c2)
max[
= 1. If the
magnetic field is
close to equipartition, synchrotron cooling is effective for the
electrons (except insofar as it is inhibited by self-absorption);
Comptonization is important whenever
(k Te / me c2)
max[
 ,
,

 2] > 1. This
diagram helps us to understand the detailed results derived for
various specific cases.
k
2] > 1. This
diagram helps us to understand the detailed results derived for
various specific cases.
k
3.1. Spherical Accretion
The specific angular momentum of accreted material is likely to
control the flow pattern, especially when close to the
hole. Nevertheless, it is worthwhile to start off with the simpler
case of spherically symmetric accretion. Some of the quantities
derived in this section (for relative time scales, etc.) can,
moreover, be straightforwardly scaled to cases where inflow occurs at
some fraction  of the
free-fall speed.
of the
free-fall speed.
If the inflow is laminar, then the only energy available for
radiation is that derived from PdV work; therefore, any smooth inflow
at high Mach number is certain to be inefficient irrespective of the
radiation mechanism. Higher efficiency is possible if the Mach number
is maintained at a value of order unity, or if there is internal
dissipation (83).
However, the fact that the bremsstrahlung cross section is only
~  f
f
 T means that this
mechanism alone can never be
operative on the free-fall time unless
T means that this
mechanism alone can never be
operative on the free-fall time unless
 >> 1, in which case (from
Equation 14) most of the radiation is swallowed by the hole. Several
authors have discussed the important effects of Comptonization. If the
only photons are those from bremsstrahlung, then merely a logarithmic
factor is gained in the radiative efficiency. However, if the magnetic
field is comparable with the value corresponding to full equipartition
with bulk kinetic energy, then photons emitted at harmonics of the
cyclotron frequency can be Comptonized up to energies such that
h
>> 1, in which case (from
Equation 14) most of the radiation is swallowed by the hole. Several
authors have discussed the important effects of Comptonization. If the
only photons are those from bremsstrahlung, then merely a logarithmic
factor is gained in the radiative efficiency. However, if the magnetic
field is comparable with the value corresponding to full equipartition
with bulk kinetic energy, then photons emitted at harmonics of the
cyclotron frequency can be Comptonized up to energies such that
h
 kT. The most
detailed work on this problem is that of Maraschi and
collaborators (42,
80):
the calculated spectrum is a power law of
slope ~ - 1 extending upward from the cyclotron/synchrotron
self-absorption turnover to the gamma-ray band.
kT. The most
detailed work on this problem is that of Maraschi and
collaborators (42,
80):
the calculated spectrum is a power law of
slope ~ - 1 extending upward from the cyclotron/synchrotron
self-absorption turnover to the gamma-ray band.
When a high luminosity L emerges from
r  rg, Compton heating or
cooling of material at larger r can create important feedback on the
flow (45,
92).
If the central source emits power
L(
rg, Compton heating or
cooling of material at larger r can create important feedback on the
flow (45,
92).
If the central source emits power
L( )
d
)
d at
frequencies between
at
frequencies between
 +
d
+
d , then Compton processes
tend to establish an electron temperature such that
, then Compton processes
tend to establish an electron temperature such that
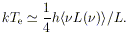
| (15)
|
(This formula strictly applies only if
h < me
c2 for all the
radiation, and if induced processes can be neglected.) The time scale
for this temperature to be established is
< me
c2 for all the
radiation, and if induced processes can be neglected.) The time scale
for this temperature to be established is
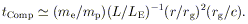
| (16)
|
If tComp(r) <
tinflow(r), and if no other heating or
cooling processes
come into play, the consequences depend on whether
kTe 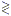 kTvirial =
mp c2(r /
rg)-1 .
If Te < Tvirial, then the inflow
must be supersonic, with the
pressure support unimportant. Conversely, if there is a range of r
where tComp < tinflow but
Te > Tvirial,
steady inflow is impossible: if the
flow were constrained to remain spherically symmetrical, "limit cycle"
behavior would develop; but in more general geometry, inflow in some
directions could coexist with out-flow in others
(18,
19).
kTvirial =
mp c2(r /
rg)-1 .
If Te < Tvirial, then the inflow
must be supersonic, with the
pressure support unimportant. Conversely, if there is a range of r
where tComp < tinflow but
Te > Tvirial,
steady inflow is impossible: if the
flow were constrained to remain spherically symmetrical, "limit cycle"
behavior would develop; but in more general geometry, inflow in some
directions could coexist with out-flow in others
(18,
19).
A characteristic feature of the region where
kTi >> me c2
is that the
electron-ion coupling time is so long that equality of the electron and
ion temperatures is not guaranteed. For low
 , the collisional
mean free paths for each species may exceed r (see
Figure 2), though even a
very
weak magnetic field would suffice to make the inflow fluidlike.
However, if there were no such field at all, then each electron or ion
could orbit the hole many times between collisions (a situation
resembling stellar dynamics around a massive central object): the net
inflow velocity would be
<< c(r / rg)-1/2, and
the density (and hence the
radiative efficiency) would be higher than for the fluidlike free-fall
solution with the same value of
, the collisional
mean free paths for each species may exceed r (see
Figure 2), though even a
very
weak magnetic field would suffice to make the inflow fluidlike.
However, if there were no such field at all, then each electron or ion
could orbit the hole many times between collisions (a situation
resembling stellar dynamics around a massive central object): the net
inflow velocity would be
<< c(r / rg)-1/2, and
the density (and hence the
radiative efficiency) would be higher than for the fluidlike free-fall
solution with the same value of
 (85).
(85).
Material infalling toward a collapsed object obviously eventually
encounters the relativistic domain (51). It is therefore necessary to
take note of what general relativity tells us about black holes; this
is done in the next section.
4. BLACK HOLES ACCORDING TO GENERAL RELATIVITY
The physics of dense star clusters and of supermassive objects are
complex and poorly understood. In contrast, the final state of such
systems - if gravitational collapse indeed occurs - is comparatively
simple, at least if we accept general relativity. According to the
so-called no-hair theorems, the endpoint of a gravitational collapse,
however messy and asymmetrical it may have been, is a standardized
black hole characterized by just two parameters - mass and spin - and
described exactly by the Kerr metric. If the collapse occurred in a
violent or sudden way, it would take several dynamical time scales for
the hole to settle down; during that period, gravitational waves would
be emitted. But the final state would still be the Kerr solution,
unless the material left behind constituted a strong
perturbation. [The perturbation due to the infalling material in
steady accretion flows is a negligible perturbation by a wide margin
of order (rg / c) / tE.]
The expected spin of the hole - an important influence on its
observable manifestations - depends on the route by which it formed
(see Figure 1). A precursor spinning
fast enough to be significantly
flattened by rotational effects when its radius was
>> rg would
probably have more specific angular momentum than the critical value
GM/c. A massive black hole that forms "in one go" is thus
likely to
have been fed with as much spin as it can accept and to end up near
the top of the range of angular momentum permitted by the Kerr metric;
the same is true for holes that grow by gradual accretion of infalling
galactic gas (11)
(though the expectation is less clear if they grow
by tidal disruption of stars). We should therefore take full
cognizance of the distinctive properties of spinning black holes.
4.1. The Kerr Metric
The Kerr metric changes its character, and the event horizon
disappears, if the specific angular momentum
J = Jmax = GM / c. The
so-called cosmic censorship hypothesis would then require that holes
always form with
J < Jmax. The Kerr solution then has a
critical radius
called the static limit, within which particles must corotate with the
hole, though they can still escape. This arises because the
frame-dragging is so strong that even light cones necessarily point in
the  direction. This critical
surface, with equatorial radius
direction. This critical
surface, with equatorial radius
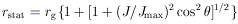
| (17)
|
is not the event horizon itself; the latter occurs at a smaller
radius. The region between the event horizon
(r = rEH) and the
static
limit is called the "ergosphere," because one can in principle extract
energy from it via a process first proposed by Penrose
(96): a
particle entering the ergosphere can split in two in such a way that
one fragment falls into the hole, but the other leaves the ergosphere
with more energy than the original particle. The extra energy comes
from the hole itself. A Kerr hole can be considered to have two kinds
of mass-energy: a fraction associated with its spin, which can be
extracted via the Penrose process, and an "irreducible" mass
(14,
41).
The fraction that can in principle be extracted is
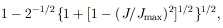
| (18)
|
which is 29% for a maximally rotating hole. The above limit is an
instance of a general theorem in black hole physics, according to
which the area of the event horizon (a quantity analogous to entropy)
can never decrease: a Kerr hole has smaller surface area than a
Schwarzschild hole of the same mass. There have been various attempts
to incorporate Penrose-style energy extraction into a realistic
astrophysical model (64,
100).
Those mechanisms that involve particle
collisions or scattering operate only for a special subset of
trajectories (14),
and they would be swamped by accompanying
processes. However, a process involving electromagnetic effects
- the Blandford-Znajek mechanism
(29)
- seems more promising (and is discussed further below and in
Section 5).
ORBITS The binding energy per unit mass for a circular
orbit of radius around a Schwarzschild hole (with J = 0) is
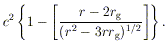
| (19)
|
For r >> rg this reduces to G
M/2r, which is just the Newtonian binding
energy. However, the binding energy has a maximum of 0.057c for an
orbit at
rmin = 6rg, with angular momentum
 min =
2
min =
2 3 rg
c. Circular
orbits closer in than this have more angular momentum and are less
tightly bound (as for orbits in classical theory when the effective
force law is
3 rg
c. Circular
orbits closer in than this have more angular momentum and are less
tightly bound (as for orbits in classical theory when the effective
force law is
 r-n,
with n > 3): the orbits have zero
binding energy for
r = 4rg (with corresponding angular momentum
r-n,
with n > 3): the orbits have zero
binding energy for
r = 4rg (with corresponding angular momentum
 0 =
4rg c); and for
r = 3rg, the expression (19.) goes to
infinity, which implies that
photons can move in circular orbits at this radius. In the Kerr
metric, the behavior of orbits depends on their orientation with
respect to the hole and on whether they are corotating or
counterrotating (14).
For corotating equatorial orbits, the innermost
stable orbit moves inward (as compared with the Schwarzschild case);
it becomes more tightly bound, with a smaller
0 =
4rg c); and for
r = 3rg, the expression (19.) goes to
infinity, which implies that
photons can move in circular orbits at this radius. In the Kerr
metric, the behavior of orbits depends on their orientation with
respect to the hole and on whether they are corotating or
counterrotating (14).
For corotating equatorial orbits, the innermost
stable orbit moves inward (as compared with the Schwarzschild case);
it becomes more tightly bound, with a smaller
 min. For
(J/Jmax) > 0.94,
rmin actually lies within the ergosphere. As
J -> Jmax the stable
corotating orbits extend inward toward
r = rg, and their binding
energy approaches
(1 - 3-1/2)c = 0.42c. These numbers determine the
maximum theoretical efficiency of accretion disks.
min. For
(J/Jmax) > 0.94,
rmin actually lies within the ergosphere. As
J -> Jmax the stable
corotating orbits extend inward toward
r = rg, and their binding
energy approaches
(1 - 3-1/2)c = 0.42c. These numbers determine the
maximum theoretical efficiency of accretion disks.
4.2. Three Astrophysically Important Relativistic
Effects
THE MINIMUM ANGULAR MOMENTUM An important inference from
the above is that there are no stationary
bound orbits whose angular momentum is less than a definite threshold
value: particles whose angular momentum is too low plunge directly
into the hole. This qualitative feature of the orbits means that no
stationary axisymmetric flow pattern can extend too close to the
rotation axis of a black hole (even well away from the equatorial
plane) - no such constraint arises for flows around an object with a
"hard" surface. Many authors have suggested that the resultant
"funnels" play a role in the initial bifurcation and collimation of jets.
LENSE-THIRRING PRECESSION An orbit around a
spinning (Kerr) hole that does not lie in the
equatorial plane precesses around the hole's spin axis with an angular
velocity [discussed by Bardeen & Petterson
(13)] of
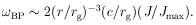
| (20)
|
This precession has a time scale longer than the orbital
period by a
factor of ~ (r / rg)3/2(J /
Jmax)-1. However,
if material spirals slowly
inward (at a rate controlled by viscosity) in a time much exceeding
the orbital time, then the effects of this precession can mount
up. The important consequence follows that the flow pattern near a
black hole, within the radius where
2 /
/
 BP, is less
than the inflow
time, can be axisymmetric with respect to the hole irrespective of the
infalling material's original angular momentum vector. The
Lense-Thirring precession, an inherently relativistic effect, thus
guarantees that a wide class of flow patterns near black holes will be
axisymmetric - an important simplification of the problem.
BP, is less
than the inflow
time, can be axisymmetric with respect to the hole irrespective of the
infalling material's original angular momentum vector. The
Lense-Thirring precession, an inherently relativistic effect, thus
guarantees that a wide class of flow patterns near black holes will be
axisymmetric - an important simplification of the problem.
ELECTROMAGNETIC PROPERTIES OF BLACK HOLES
Interactions of black holes with magnetic fields imposed on their
surroundings can have important astrophysical effects. When a hole
forms from collapsing magnetized material, the magnetic field outside
the horizon decays ("redshifts away") on the collapse time scale
rg / c. But if, for instance, an external
electric field were applied to
a Schwarzschild hole, then after transients had decayed, a modified
field distribution would be established where the electric field
appeared to cross the horizon normally. The event horizon (or
"surface") of the hole thus behaves in some respects like a conductor
(47,
76,
134).
It does not have perfect conductivity, however: if it
did, electromagnetic flux would never be able to penetrate the
horizon. Comparing the decay time scale for transients around a black
hole (rg / c) with the time scale
(rg2 /
4
 ) appropriate to a sphere of
radius rg and conductivity
) appropriate to a sphere of
radius rg and conductivity
 , we can associate a surface
resistivity
of 377
, we can associate a surface
resistivity
of 377  with the
horizon. This analogy can be put on a more rigorous
basis (134),
and the "resistance" of a black hole is found to be
ZH
with the
horizon. This analogy can be put on a more rigorous
basis (134),
and the "resistance" of a black hole is found to be
ZH  100
ohms. More generally, a Kerr black hole behaves like a
spinning conductor. A simple discussion
(98) valid for
J << Jmax shows
that a
hole embedded in a uniform magnetic field B0 would
acquire a quadrupole distribution of electric charge
100
ohms. More generally, a Kerr black hole behaves like a
spinning conductor. A simple discussion
(98) valid for
J << Jmax shows
that a
hole embedded in a uniform magnetic field B0 would
acquire a quadrupole distribution of electric charge
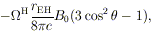
| (21)
|
where
 H = (J /
Jmax) c / 2rEH is
the effective angular velocity of the hole.
The corresponding poloidal electric field in a nonrotating frame is
H = (J /
Jmax) c / 2rEH is
the effective angular velocity of the hole.
The corresponding poloidal electric field in a nonrotating frame is
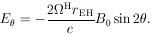
| (22)
|
Just as in a classical "unipolar inductor," power can be extracted
by allowing a current flow between a spinning hole's equator and
poles. The maximum electric potential drop is
~ B0 rg(J /
Jmax), where B0
is the imposed field. This can be very large, as it is when a similar
argument is applied to spinning magnetized neutron stars in
conventional models for pulsars.
For the fiducial field strength BE (Equation 6), this
emf is
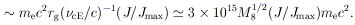
| (23)
|
A single test charge introduced into this electromagnetic
field will
extract from the hole an energy of this order. However, the
magnetosphere is unlikely just to contain a few "test charges";
indeed, the bare minimum charge density needed to modify the imposed
field is
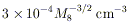
| (24)
|
(cf. Equation 12), and pair production generates far more
charges than
this (see Section 5). Just as in pulsars
(8), a realistic
magnetospheric current system and plasma distribution, though very
hard to calculate, is likely to "short-out" the electric field. A
relevant parameter is then
 H, the angular
velocity of the field lines
at large distance from the hole. This is related to the ratio of the
effective resistance
Z
H, the angular
velocity of the field lines
at large distance from the hole. This is related to the ratio of the
effective resistance
Z to the
resistance of the hole ZH:
to the
resistance of the hole ZH:
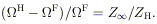
| (25)
|
In the charge-starved limit, corresponding to infinite
resistance at infinity,
 F = 0. The
"matched" case when
Z
F = 0. The
"matched" case when
Z =
ZF(
=
ZF( F =
½
F =
½  H)
corresponds to the maximum power extraction for a given
B0. This power is of order
H)
corresponds to the maximum power extraction for a given
B0. This power is of order
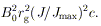
| (26)
|
The efficiency in this case is lower than when
Z ->
->
 (zero power), in
the sense that half of the power is dissipated in the hole, and raises
its irreducible mass; nevertheless, 9.2% of the rest energy could be
extracted while slowing down a hole that started off with
J = Jmax.
(zero power), in
the sense that half of the power is dissipated in the hole, and raises
its irreducible mass; nevertheless, 9.2% of the rest energy could be
extracted while slowing down a hole that started off with
J = Jmax.
Electromagnetic extraction of energy from black holes seems a
realistic and important possibility. Its astrophysical context is
discussed in Section 5.
SUMMARY The results of this section can be summarized by
saying that three
distinctively relativistic features of black holes are important in
models for galactic nuclei:
- There is a definite lower limit to the angular momentum of any
stably orbiting material.
- The Lense-Thirring precession enforces axisymmetry on any
inward-spiraling flow pattern near the hole; consequently, any
directed outflow initiated in the relativistic domain will be aligned
with the hole's spin axis and will squirt in a constant direction
(irrespective of the provenance of the infalling gas), except insofar
as precession or accretion processes can reorient the hole's spin
(105).
- A rotating hole's latent spin energy can be tapped by externally
applied magnetic fields; this can provide a power source far exceeding
that from the accretion process itself.
5. ACCRETION FLOWS WITH ANGULAR MOMENTUM
5.1. Origin of Infalling Matter
The accreted material could fall in from the body of the galaxy (gas
expelled from ordinary stars via stellar winds and supernovae); it
could even come from intergalactic clouds captured by the
galaxy. [Relevant here is the evidence that galaxies are more likely
to be active if they are interacting with a neighbor
(10,
43), and
that quasars may be in interacting galaxies
(62).] Alternatively, the
gas supply may originate in the central parts of the galaxy: e.g. (a)
debris from stars tidally disrupted by the hole
(60,
61); (b) debris
from stellar collisions in a compact star cluster around the hole
(52);
or (c) a positive feedback process whereby stars are induced to
lose mass (and thereby provide further fuel) by irradiation from a
luminous central source
(82).
The accretion flow pattern depends on the angular momentum of the
infalling gas: if this is large and has a steady orientation, then an
accretion disk may extend out to very large values of
(r/rg); but the
Lense-Thirring effect renders the flow pattern near the hole (where
the power is primarily released) insensitive to conditions at large
r,
provided only that the matter has enough angular momentum to prevent
it from falling directly into the hole. Accretion disks have been
reviewed by Pringle (101)
in a general astronomical context; I
summarize here some new developments insofar as they may relate to
massive holes in galactic nuclei.
5.2. Thin Disks
The simplest hypothesis is that the central object is being fueled
steadily via an accretion disk
(35,
73,
117). The standard thin
disk
model assumes that the gas at each radius is in a nearly Keplerian
orbit. Slow radial infall occurs as viscosity transfers angular
momentum outward. Energy dissipated by the viscous stress is radiated
locally at a rate three times the local rate at which gravitational
energy is liberated
(GM dr / r
between r and r + dr). The factor of 3
arises because viscous stresses transport energy as well as angular
momentum outward. This local imbalance is globally rectified in the
innermost region of the disk, where the local release of binding
energy exceeds the dissipation. For thin disks, slow inflow can be
maintained down to the innermost stable orbit; the efficiency then
equals the fractional binding energy for this orbit.
dr / r
between r and r + dr). The factor of 3
arises because viscous stresses transport energy as well as angular
momentum outward. This local imbalance is globally rectified in the
innermost region of the disk, where the local release of binding
energy exceeds the dissipation. For thin disks, slow inflow can be
maintained down to the innermost stable orbit; the efficiency then
equals the fractional binding energy for this orbit.
A disk has a scale height h normal to the orbital plane such that
(h / r)  cs / vvirial, where
cs is the internal sound speed, and is "thin" if
this is << 1. One can write
cs / vvirial, where
cs is the internal sound speed, and is "thin" if
this is << 1. One can write
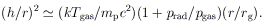
| (27)
|
In this expression, Tgas is the gas temperature in
the plane of
symmetry (which could significantly exceed the surface temperature if
the optical depth were very large); the quantity on the right-hand
side is essentially the ratio of thermal and gravitational
energies. Generally, the vertical support is provided by gas pressure
at large r and for low accretion rates
(116). Disks with high
 are
strongly radiation dominated in their inner regions: this is more true
when the central hole is supermassive than for a stellar-mass hole
because [for a given
L / LE, and thus a given (h / r)] the
gas pressure per particle, proportional to
Tgas (cf. Equation 5), scales as
M-1/4.
are
strongly radiation dominated in their inner regions: this is more true
when the central hole is supermassive than for a stellar-mass hole
because [for a given
L / LE, and thus a given (h / r)] the
gas pressure per particle, proportional to
Tgas (cf. Equation 5), scales as
M-1/4.
The very simplest models for such disks predict a thermal spectrum
typically peaking in the ultraviolet (cf. Equation 5); they thus
cannot in themselves account for the very broadband radiation from
galactic nuclei. But the major uncertainties in the theory of these
disks are the interlinked questions of viscosity and magnetic
fields. These fields, amplified by shearing motions
(49) and possibly
by turbulence-driven dynamo action
(102,
103), probably provide the
main viscosity. Only crude estimates can be made of the resultant
 -parameter. Moreover, it is
unclear whether the magnetic stresses
build up to a fixed fraction of the total pressure or only of the gas
pressure. The argument for the latter view
(44,
110,
111) is that
large-amplitude density contrasts can be induced as soon as magnetic
stresses become competitive with gas pressure, and buoyancy effects
then elevate the flux into the disk's "corona," impeding further
amplification. This can happen, however, only if the radiation is able
to diffuse relative to the gas: in the limit of very large optical
depths, the field could be amplified by differential rotation on time
scales much shorter than those on which density inhomogeneities could
develop. Gas and radiation would then act like a single composite
fluid, and only the total pressure would be relevant. The answer to
this somewhat confusing (though well-posed) theoretical question makes
a big numerical difference to the inward drift time scale; more
importantly, it determines whether such a disk would be unstable to
the "visco-thermal" instability
(101).
-parameter. Moreover, it is
unclear whether the magnetic stresses
build up to a fixed fraction of the total pressure or only of the gas
pressure. The argument for the latter view
(44,
110,
111) is that
large-amplitude density contrasts can be induced as soon as magnetic
stresses become competitive with gas pressure, and buoyancy effects
then elevate the flux into the disk's "corona," impeding further
amplification. This can happen, however, only if the radiation is able
to diffuse relative to the gas: in the limit of very large optical
depths, the field could be amplified by differential rotation on time
scales much shorter than those on which density inhomogeneities could
develop. Gas and radiation would then act like a single composite
fluid, and only the total pressure would be relevant. The answer to
this somewhat confusing (though well-posed) theoretical question makes
a big numerical difference to the inward drift time scale; more
importantly, it determines whether such a disk would be unstable to
the "visco-thermal" instability
(101).
Magnetic fields may also have a big effect on the radiation spectrum
emerging from a realistic thin disk. Energy transported by magnetic
buoyancy into a hot corona could dominate the (approximately
blackbody) radiation from the dense part of the disk. Magnetic flares
in the corona may accelerate relativistic electrons that radiate
nonthermally.
Blandford (24)
has emphasized that there is no obvious ultimate
repository from the angular momentum of disks in galactic nuclei
(whereas the companion star and the orbit serve this role for binary
star systems). If the magnetic field were sufficiently well ordered, a
coronal wind (rather than outward transfer via viscosity within the
disk itself) could be the main sink for the angular momentum of
accreted material (23,
26).
An alternative resolution of the problem, suggested by Ostriker
(91),
is that the angular momentum is
transferred via dynamical friction to a star cluster in which the disk
is embedded.
Most of the recent theoretical work on thin disk structure is aimed
primarily at understanding cataclysmic variables, X-ray binaries,
etc., but it is relevant also in the galactic nucleus context. In all
disks, the thermal balance of the outer parts is likely to be
controlled by irradiation (causing photoionization, Compton heating,
etc.) from the central region. Even where such disks exist, they could
be embedded in hotter quasi-spherical structures. There may thus be no
clear demarcation in the real world between thin disks and the
toroidal structures to which we next turn.
5.3. General Structure of Tori or Thick Disks
Disks become geometrically thick, with
h  r, if the
internal pressure builds up so that
cs
r, if the
internal pressure builds up so that
cs  (GM / r)1/2. This can happen
either because
radiation pressure becomes competitive with gravity or because the
material is unable to radiate the energy dissipated by viscous
friction, which then remains as internal energy. Before discussing the
(very different) internal physical conditions in these two kinds of
tori, let us consider their general equilibrium structure.
(GM / r)1/2. This can happen
either because
radiation pressure becomes competitive with gravity or because the
material is unable to radiate the energy dissipated by viscous
friction, which then remains as internal energy. Before discussing the
(very different) internal physical conditions in these two kinds of
tori, let us consider their general equilibrium structure.
In thick disks, radial pressure gradients cannot be ignored; the
angular velocity is therefore not Keplerian and becomes (within
certain constraints) a free parameter. Uncertainty about the viscosity
is a major stumbling block. This uncertainty is not crucial to many
qualitative features of thin disks (e.g. their overall energetics).
However, in thick disks one must deal explicitly with shear stresses
in two directions. The stresses determine the distributions both of
angular momentum and enthalpy, and therefore the shape of the isobars
inside the disk; internal circulation patterns may be important for
energy transport. There is always a pressure maximum at
r = rmax in the
equatorial plane. Outside
rmax, the angular velocity is
sub-Keplerian, but for
r < rmax it is faster than Keplerian. Such
structures around
Kerr holes were investigated by Bardeen
(12) and by Fishbone &
Moncrief
(50;
see also 36,
37).
Recent work, from a more astrophysical
viewpoint, has been spearheaded by Abramowicz and colleagues
(1 -
3,
63,
65,
93,
129).
They have exploited an important simplifying feature:
the shape of a torus depends only on its surface distribution of
angular momentum. If the angular velocity
 (
( ) is given as a function
of angular momentum
) is given as a function
of angular momentum  , then
the surface binding energy U is given implicitly by
, then
the surface binding energy U is given implicitly by
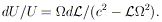
| (28)
|
A simple special case is that for which
 is the same
everywhere. The binding energy is then constant over the whole surface
of the torus; there is thus, for each value of
is the same
everywhere. The binding energy is then constant over the whole surface
of the torus; there is thus, for each value of
 , a family of such
tori, parametrized by the surface binding energy U. As U
tends to
zero, the tori "puff up," and the part of the surface close to the
rotation axis acquires a paraboloidal shape. The gravitational field
is essentially Newtonian throughout most of the volume, but
relativistic effects come in near the hole if
, a family of such
tori, parametrized by the surface binding energy U. As U
tends to
zero, the tori "puff up," and the part of the surface close to the
rotation axis acquires a paraboloidal shape. The gravitational field
is essentially Newtonian throughout most of the volume, but
relativistic effects come in near the hole if


 min, the angular
momentum of the smallest stable orbit. For
min, the angular
momentum of the smallest stable orbit. For
 in the range
in the range
 min <
min <
 <
<
 0, special
significance attaches to the torus for which U exactly
equals the binding energy of the (unstable) orbit of angular momentum
0, special
significance attaches to the torus for which U exactly
equals the binding energy of the (unstable) orbit of angular momentum
 . There is then a cusplike
inner edge, across which material can
spill over into the hole (just as material leaves a star that just
fills its Roche lobe in a binary system). This particular relation
between U and
. There is then a cusplike
inner edge, across which material can
spill over into the hole (just as material leaves a star that just
fills its Roche lobe in a binary system). This particular relation
between U and  would approximately prevail at the inner edge of any
torus where quasi-steady accretion is going on (see
Figure 3 and caption).
would approximately prevail at the inner edge of any
torus where quasi-steady accretion is going on (see
Figure 3 and caption).
More generally, one can consider
(99)
tori where  goes as some
power of
goes as some
power of  . Such tori exist
in all cases where the increase of angular
momentum with
. Such tori exist
in all cases where the increase of angular
momentum with  is slower
than Keplerian. The funnels tend to be
conical rather than paraboloidal if the rotation law is nearer to
Keplerian; they extend closer to
r = rg when the black hole is
rapidly rotating.
is slower
than Keplerian. The funnels tend to be
conical rather than paraboloidal if the rotation law is nearer to
Keplerian; they extend closer to
r = rg when the black hole is
rapidly rotating.
Accretion flows where high internal pressures guarantee
h  r [from
(27.)] could resemble such tori if the viscosity parameter were low
enough that the flow was essentially circular, and provided also that
the configuration were stable (though there is frankly no firm basis
for confidence in either of these requirements).
r [from
(27.)] could resemble such tori if the viscosity parameter were low
enough that the flow was essentially circular, and provided also that
the configuration were stable (though there is frankly no firm basis
for confidence in either of these requirements).
A generic feature of accretion tori is that they are less efficient
- in the sense that they liberate less energy per gram of infalling
matter - than thin disks. The efficiency is given by the binding
energy of the material at the cusp; this depends on the angular
momentum profile (via Equation 28), but for an
 = constant torus of
outer radius r0, it is
(r0 / rg)-1, which
implies very low efficiency for large tori.
= constant torus of
outer radius r0, it is
(r0 / rg)-1, which
implies very low efficiency for large tori.
In any torus with
r0 >> rg and a strongly
sub-Keperlian rotation law,
rotation is unimportant (gravity being essentially balanced by
pressure gradients, and the isobars almost spherical) except near the
funnel along the rotation axis. To avoid convective instability, the
density must fall off with radius at least as steeply as the
isentropic laws
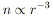
| (29)
|
for  = 4/3 (e.g. radiation
pressure support), and
= 4/3 (e.g. radiation
pressure support), and
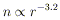
| (30)
|
for  = 5/3 (e.g. ion
pressure support).
= 5/3 (e.g. ion
pressure support).
The two very different cases of radiation-supported and
ion-supported tori may incorporate elements of a valid model for some
classes of galactic nuclei. I discuss them here in turn, and then (in
Section 6) I consider another question: whether
the "funnels" in such
flow patterns are important in collimating the outflowing jet material.
The foregoing discussion begs the question of whether these tori are
stable and whether stability requirements narrow down the possible
forms for
 (
( ). Local instabilities can
arise from unfavorable entropy and angular momentum gradients
(66,
115).
These presumably evolve to
create marginally stable convection zones, as in a star. Dynamically
important magnetic fields may induce further instabilities. Moreover,
tori may be seriously threatened by nonaxisymmetric
instabilities. Papaloizou & Pringle
(94)
recently demonstrated that an
). Local instabilities can
arise from unfavorable entropy and angular momentum gradients
(66,
115).
These presumably evolve to
create marginally stable convection zones, as in a star. Dynamically
important magnetic fields may induce further instabilities. Moreover,
tori may be seriously threatened by nonaxisymmetric
instabilities. Papaloizou & Pringle
(94)
recently demonstrated that an
 = constant toroidal
configuration marginally stable to axisymmetric
instabilities possesses global, nonaxisymmetric dynamical
instabilities, which would operate on a dynamic time scale. It is not
clear to what extent more general angular momentum distributions are
similarly vulnerable, but it may turn out that funnel regions where
pressure gradients are balanced by centrifugal effects rather than by
gravity are never dynamically stable.
= constant toroidal
configuration marginally stable to axisymmetric
instabilities possesses global, nonaxisymmetric dynamical
instabilities, which would operate on a dynamic time scale. It is not
clear to what extent more general angular momentum distributions are
similarly vulnerable, but it may turn out that funnel regions where
pressure gradients are balanced by centrifugal effects rather than by
gravity are never dynamically stable.
5.4. Radiation-Supported Tori
A thick structure can be supported by radiation pressure only if it
radiates at
L  LE. Indeed, in any configuration supported in this
way, not only the total luminosity but its
distribution over the surface is determined by the form of the
isobars. Tori with long
narrow funnels have the property that their total luminosity can
exceed LE by a logarithmic factor
(118).
More interestingly, most of
this radiation escapes along the funnel, where centrifugal effects
make the "surface gravity" (and hence the leakage of radiation) much
larger than over the rest of the surface. If accretion powers such a
torus, then
LE. Indeed, in any configuration supported in this
way, not only the total luminosity but its
distribution over the surface is determined by the form of the
isobars. Tori with long
narrow funnels have the property that their total luminosity can
exceed LE by a logarithmic factor
(118).
More interestingly, most of
this radiation escapes along the funnel, where centrifugal effects
make the "surface gravity" (and hence the leakage of radiation) much
larger than over the rest of the surface. If accretion powers such a
torus, then
 × (efficiency)
× (efficiency)
 10.
10.
If the outer parts are sufficiently slowly rotating that (29.), or a
still steeper law, approximately holds, the characteristic Thomson
optical depth must depend on radius r at least as steeply as
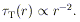
| (31)
|
This in turn implies that the torus cannot remain optically thick (in
the sense that
 T > 1) out to
r >> rg unless the
viscosity parameter
T > 1) out to
r >> rg unless the
viscosity parameter  at
r
at
r  rg is very low indeed. (This has been thought by
some to be an
implausible feature of such models. However, one could argue
contrariwise that these objects resemble stars, in which the
persistence of differential rotation certainly implies an exceedingly
low effective
rg is very low indeed. (This has been thought by
some to be an
implausible feature of such models. However, one could argue
contrariwise that these objects resemble stars, in which the
persistence of differential rotation certainly implies an exceedingly
low effective  . Pursuing
this analogy further suggests that
large-scale circulation effects may play as big a role in energy
transport as radiative diffusion does.)
. Pursuing
this analogy further suggests that
large-scale circulation effects may play as big a role in energy
transport as radiative diffusion does.)
If LTE prevails in such a torus, then the temperature at radius r,
at locations well away from the rotation axis, is
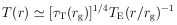
| (32)
|
(cf. Equation 5). The condition for LTE [i.e. that photons can be
thermalized within their diffusion time scale
 T(r)(r
/ c)] is more stringent than
T(r)(r
/ c)] is more stringent than
 T > 1. Indeed,
even at the pressure maximum
(r
T > 1. Indeed,
even at the pressure maximum
(r  rg), the requirement is
rg), the requirement is
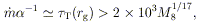
| (33)
|
and radiation pressure dominates gas pressure by a factor of
~ 106
[ T
(rg)]-1/4 M81/4
- much larger than ever occurs in stellar structure. If
T
(rg)]-1/4 M81/4
- much larger than ever occurs in stellar structure. If
 T(rg) is even larger than (33.),
so that LTE prevails out to
r >> rg,
the hole may be sufficiently well smothered that all the radiation
effectively emerges from a photosphere, in appearance rather like an O
or B star (24).
T(rg) is even larger than (33.),
so that LTE prevails out to
r >> rg,
the hole may be sufficiently well smothered that all the radiation
effectively emerges from a photosphere, in appearance rather like an O
or B star (24).
5.5. Ion-Supported Tori
We have seen that for spherically symmetric inflow, the cooling time
scale - and even the electron-ion coupling time - can be longer than
the free-fall time; the same conditions can prevail even for inflow
with angular momentum, provided that
 is low enough. As
compared with
Figure 2, all that is changed is that
the inflow time is
is low enough. As
compared with
Figure 2, all that is changed is that
the inflow time is
 -1
tfree - fall and
the characteristic density for a given
-1
tfree - fall and
the characteristic density for a given
 is higher by
is higher by
 -1. The
condition for electron-ion coupling to be ineffective in the inner
parts of a torus (cf. Figure 2) is
-1. The
condition for electron-ion coupling to be ineffective in the inner
parts of a torus (cf. Figure 2) is
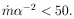
| (34)
|
When (34.) holds, the ions can remain at the virial temperature even
if synchrotron and Compton processes permit the electrons to cool, and
the disk swells up into a torus. The dominant viscosity is likely to
be magnetic. Estimates of magnetic viscosity are very uncertain;
Eardley & Lightman
(49) suggest that
 falls in the range
0.01 - 1.0. However, there is no reason why the magnetic
falls in the range
0.01 - 1.0. However, there is no reason why the magnetic
 should fall
as
should fall
as  is reduced, so (34.)
should definitely be fulfilled for sufficiently low accretion rates.
is reduced, so (34.)
should definitely be fulfilled for sufficiently low accretion rates.
An accretion flow where  is
small, and where (furthermore) the
radiative efficiency is low, may seem a doubly unpromising model for
any powerful galactic nucleus. However, such a torus around a spinning
black hole offers an environment where the Blandford-Znajek
(29)
process could operate
(108).
Even though it may not radiate much
directly, the torus can then serve as a catalyst for tapping the
hole's latent spin energy. Three conditions are necessary:
is
small, and where (furthermore) the
radiative efficiency is low, may seem a doubly unpromising model for
any powerful galactic nucleus. However, such a torus around a spinning
black hole offers an environment where the Blandford-Znajek
(29)
process could operate
(108).
Even though it may not radiate much
directly, the torus can then serve as a catalyst for tapping the
hole's latent spin energy. Three conditions are necessary:
1. Magnetic fields threading the hole must be maintained by an
external current system. The requisite flux could have been advected
in by slow accretion; even if the field within the torus were tangled,
it would nevertheless be well ordered in the magnetosphere. The torus
would be a good enough conductor to maintain surface currents in the
funnel walls, which could confine such a field within the hole's
magnetosphere. The only obvious upper limit to the field is set by the
requirement that its total energy should not exceed the gravitational
binding energy of the torus. (An equivalent statement is that B
should not exceed  1/2
1/2
 -1/2
BE)
-1/2
BE)
2. There must be a current flowing into the hole. Although an
ion-supported torus radiates very little, it emits some bremsstrahlung
gamma rays. Some of these will interact in the funnel to produce a
cascade (31)
of electron-positron pairs
(99,
108),
yielding more than
enough charge density to "complete the circuit" and carry the
necessary current - enough, indeed, to make the magnetosphere
essentially charge-neutral, in the sense that
(n+ + n-) >>
|(n+ - n-)|,
so that relativistic MHD can be applied.
3. The proper "impedance match" must be achieved between the hole and
the external resistance. Phinney
(99)
has explored the physics of the
relativistic wind, whose source is the pair plasma created in the
magnetosphere and that flows both outward along the funnel and into
the hole. By considering the location of the critical points, he finds
consistent wind solutions where
 F is as large as 0.2
F is as large as 0.2
 H. This
corresponds (cf. Equation 25) to 60% of the maximum power extraction
(for a given B-field). Although some energy is dissipated in the
hole,
this would still permit a few percent of the hole's rest mass energy
to be transformed into a mixture of Poynting flux and a relativistic
electron-positron outflow.
H. This
corresponds (cf. Equation 25) to 60% of the maximum power extraction
(for a given B-field). Although some energy is dissipated in the
hole,
this would still permit a few percent of the hole's rest mass energy
to be transformed into a mixture of Poynting flux and a relativistic
electron-positron outflow.
The Blandford-Znajek process could operate even if the field
threading the hole were anchored to a thin disk, but a thick
ion-supported torus provides an attractive model for strong radio
galaxies because it could initiate collimated outflow (see the
discussion in Section 6). The possibility of
such tori depends,
however, on the assumption that Coulomb scattering alone couples
electrons to ions. This raises the question of whether some collective
process might, realistically, be more efficient - if so, the electrons
could drain energy from the ions and the torus would deflate. There
are bound to be shearing motions, owing to differential rotation,
which generate local pressure anisotropies in the plasma. There are
certainly instabilities that isotropize the ion plasma, as well as
instabilities that isotropize the electron plasma. The key question -
which still seems open - is whether these two isotropization processes
act almost independently, or whether they can transfer energy from
ions to electrons.
[Although electromagnetic extraction of energy is especially
important for ion-supported tori (objects where the accretion process
is inevitably inefficient), this process could also augment the power
generated within a radiation-supported torus. There is in principle no
limit to the power that could be extracted from a spinning hole
embedded in a dense and strongly magnetized cloud, provided that this
power can escape preferentially along the rotation axis without
disrupting the cloud. These optically thick radiation-driven jets
(21),
discussed primarily in the different context of SS 433, could
occur in quasars. If the cloud were not sufficiently flattened to
permit the excess energy to escape in preferential directions,
material would be blown from the cloud, reducing its central pressure:
this condition would persist until the total (accretion plus
electromagnetic) power fell to LE, but only a fraction
came from accretion.]
6. JET FORMATION
Directed outflow is a ubiquitous feature of active galactic nuclei,
and it is also seen in some small-scale prototypes of AGNs in our own
Galaxy (e.g. SS 433). This is in itself evidence that a spherically
symmetric model cannot be entirely realistic. For a full review of
theories of jet propagation, with special relevance to radio galaxies,
the reader is referred to Begelman et al.
(17).
The direct evidence
for jets pertains exclusively to scales much larger than the primary
power source. The scales probed by VLBI are typically a few parsecs
(  104rg for plausible central masses); the
only evidence for
smaller-scale beaming comes from indirect arguments about the physics
of optically violent variables (OVVs), or "blazars"
(6,
87,
88). There
are theoretical reasons for postulating that the relativistic outflow
is initiated on scales of order rg, but there are
really no grounds
for believing that a narrow collimation angle is established
until the
jets get out to VLBI scales or beyond: indeed, conditions in the
medium
104rg for plausible central masses); the
only evidence for
smaller-scale beaming comes from indirect arguments about the physics
of optically violent variables (OVVs), or "blazars"
(6,
87,
88). There
are theoretical reasons for postulating that the relativistic outflow
is initiated on scales of order rg, but there are
really no grounds
for believing that a narrow collimation angle is established
until the
jets get out to VLBI scales or beyond: indeed, conditions in the
medium
 1 pc from the central
source cannot readily provide the kind of pressure-confined "nozzles"
(27)
that could best collimate them
(107).
1 pc from the central
source cannot readily provide the kind of pressure-confined "nozzles"
(27)
that could best collimate them
(107).
The radiation from the jets - the emission detected by VLBI and
other radio techniques, as well as the emission in other wave bands
from (for instance) the M87 jet - is presumably synchrotron radiation
from electrons accelerated in situ. Plainly, any
high- random motions
produced at
r
random motions
produced at
r  rg would have been eliminated by radiative and
adiabatic losses before the jet got out to 1 pc. In the superluminal
sources, there is direct evidence for bulk relativistic outflow
(
rg would have been eliminated by radiative and
adiabatic losses before the jet got out to 1 pc. In the superluminal
sources, there is direct evidence for bulk relativistic outflow
( b
b
 5). We do not know
whether this outflow involves ordinary matter,
electron-positron plasma, or even Poynting flux, and various authors
have suggested schemes involving each of these options.
5). We do not know
whether this outflow involves ordinary matter,
electron-positron plasma, or even Poynting flux, and various authors
have suggested schemes involving each of these options.
Any disk structure near a black hole provides a pair of preferred
directions along the rotation axis; moreover, within the
Lense-Thirring effect's domain of influence, this axis is maintained
steady by the hole's gyroscopic effect. Magnetically driven winds from
tori or from thin disks (23,
26)
could generate outflowing jets with
the attractive attribute of a self-confining toroidal field.
The evacuated vortices along the axes of thick accretion tori, which
can be very narrow for an angular momentum distribution close to
 = constant, suggest
themselves as possible preexisting channels for
directed outflow. The most widely discussed version of this idea,
first proposed by Lynden-Bell
(74),
utilizes radiation pressure. A
simple order-of- magnitude argument shows that a test particle
(electron plus ion) released from rest outside a source with
r
= constant, suggest
themselves as possible preexisting channels for
directed outflow. The most widely discussed version of this idea,
first proposed by Lynden-Bell
(74),
utilizes radiation pressure. A
simple order-of- magnitude argument shows that a test particle
(electron plus ion) released from rest outside a source with
r  rg
and (L - LE) / LE
rg
and (L - LE) / LE
 1 would attain a
relativistic speed; a
radiation-supported torus whose vortex has cone angle
1 would attain a
relativistic speed; a
radiation-supported torus whose vortex has cone angle
 emits within
this cone a greatly enhanced luminosity
~
emits within
this cone a greatly enhanced luminosity
~  -2
LE per
unit solid angle,
which suggests that this photon beam might impart high Lorentz factors
to any matter in its path.
-2
LE per
unit solid angle,
which suggests that this photon beam might impart high Lorentz factors
to any matter in its path.
Detailed study reveals flaws in this superficially attractive idea
(4,
5,
90,
119).
The main problem is that the radiation field within a
long, narrow funnel is almost isotropic: there may indeed be a
super-Eddington outward flux along it, but the radiation density far
exceeds (flux / c) because of scattering, or absorption and
reemission, by the walls. Consequently, a test electron travels
subrelativistically along the funnel, at a speed such that the
radiation appears nearly isotropic in its moving frame. The radiation
flux only becomes well collimated by the time the particle escapes
from the funnel, at r = r0. Even for the
(probably unstable)  =
constant tori, r0 is at least
=
constant tori, r0 is at least
 -2
rg; and out there the dilution
(because r is now
>> rg) cancels out the
-2
rg; and out there the dilution
(because r is now
>> rg) cancels out the
 factor
gained from the beaming. The net result is that
factor
gained from the beaming. The net result is that
 -values of only ~ 2 can be
reached
for an electron-ion plasma, and maybe up to ~ 5 for electron-positron
plasma. A second difficulty is that the Thomson depth along the funnel
would become > 1, vitiating the test-particle approach adopted in the
calculations, if the particles were numerous enough to carry a
substantial fraction of L. [However, in the limit of very large
optical depths, where radiation and matter can be treated as a single
fluid, radiation pressure around a supercritical central source - a
"cauldron" (21)
- could efficiently generate a jet of ordinary matter with high
-values of only ~ 2 can be
reached
for an electron-ion plasma, and maybe up to ~ 5 for electron-positron
plasma. A second difficulty is that the Thomson depth along the funnel
would become > 1, vitiating the test-particle approach adopted in the
calculations, if the particles were numerous enough to carry a
substantial fraction of L. [However, in the limit of very large
optical depths, where radiation and matter can be treated as a single
fluid, radiation pressure around a supercritical central source - a
"cauldron" (21)
- could efficiently generate a jet of ordinary matter with high
 b.]
b.]
Quite apart from these theoretical difficulties, models involving
radiation-supported tori cannot be relevant to the objects where the
most spectacular jets are seen (radio galaxies, M87, etc.). We have
upper limits to the thermal luminosity from these AGNs; we also have
lower limits to the energies involved in producing large-scale radio
structure and, hence, to the masses involved. Combining these limits
precludes there being any object emitting a thermal luminosity
LE (the
level of isotropic emission that would be an inevitable concomitant of
a radiation-supported torus with a narrow funnel).
An ion-supported torus maintained by accretion with low
 can
provide funnels along the rotation axis, just as a radiation-supported
torus can. The expelled material would then be an electromagnetically
driven wind of electron-positron plasma
(99,
108).
The rest mass energy of the pairs could be
<< L/c2 - indeed, most of the
outflow could
be in Poynting flux rather than being carried by the pairs themselves
- making high beam Lorentz factors
can
provide funnels along the rotation axis, just as a radiation-supported
torus can. The expelled material would then be an electromagnetically
driven wind of electron-positron plasma
(99,
108).
The rest mass energy of the pairs could be
<< L/c2 - indeed, most of the
outflow could
be in Poynting flux rather than being carried by the pairs themselves
- making high beam Lorentz factors
 b no problem. An
energy flux of
this kind could readily be converted into relativistic particles at
large distances from its point of origin and is thus an attractive
model for radio sources.
b no problem. An
energy flux of
this kind could readily be converted into relativistic particles at
large distances from its point of origin and is thus an attractive
model for radio sources.
Two factors constrain the content and the Lorentz factor of jets
emerging from scales of ~ rg
(99,
107). First, an
e+-e- jet that
started off with too high a particle density would suffer annihilation
before moving one scale height: this means that an energy flux
LE in
pair kinetic energy, rather than in Poynting flux, is impossible
unless  b is
high. [The particle flux is then less for a given L;
furthermore, the time scale available for annihilation, measured in
the moving frame, is only
b is
high. [The particle flux is then less for a given L;
furthermore, the time scale available for annihilation, measured in
the moving frame, is only
 b-1(r / c).] But
radiation drag effects give a
second countervailing constraint that precludes particle jets with
very high values of
b-1(r / c).] But
radiation drag effects give a
second countervailing constraint that precludes particle jets with
very high values of
 b. Radiation
pressure provides an acceleration
only if it comes from the backward direction after transforming into
the moving frame (97).
If radiation comes from a source of finite size
rs, then the acceleration at a distance r would
always saturate for
b. Radiation
pressure provides an acceleration
only if it comes from the backward direction after transforming into
the moving frame (97).
If radiation comes from a source of finite size
rs, then the acceleration at a distance r would
always saturate for
 b
b
 (r /
rs),
no matter how high the luminosity of the source. Moreover,
in a realistic model for a galactic nucleus, some fraction of the
luminosity is scattered or reemitted on scales out to ~ 1 pc. This
quasi-isotropic flux exerts a Compton drag force on any beam, and it
is particularly serious for e+-e- beams, which
have the least inertia
relative to their scattering cross section.
(r /
rs),
no matter how high the luminosity of the source. Moreover,
in a realistic model for a galactic nucleus, some fraction of the
luminosity is scattered or reemitted on scales out to ~ 1 pc. This
quasi-isotropic flux exerts a Compton drag force on any beam, and it
is particularly serious for e+-e- beams, which
have the least inertia
relative to their scattering cross section.
The interaction of jets with the material at ~ 1 pc in AGNs is an
interesting topic that has only recently been seriously discussed
(86).
Possibly, the beams generally deposit their energy in the
emission-line region, and only in especially favorable cases does the
jet material get collimated sufficiently to penetrate beyond
r  1 pc.
1 pc.
7. SOME COMMENTS ON PHENOMENOLOGY
7.1. The Continuum Spectrum
The only direct clue to physical conditions in the central region
(i.e. within a radius of, say, 100rg) is the rather
featureless
continuum luminosity: spectral lines originate farther out. The models
we have discussed can radiate either thermally or nonthermally:
indeed, one of the hardest things to estimate is what fraction of the
power dissipated via viscous friction in a realistic flow pattern
would go directly into ultrarelativistic particles (via shocks,
magnetic reconnection, etc.) rather than being shared among all the
particles. Unfortunately, observations are little help in
discriminating between various continuum radiation mechanisms: a
smooth spectrum could be produced equally well by several alternative
mechanisms. For instance
(99),
there are at least four ways of getting a spectrum with
L( )
)

 -1/2.
-1/2.
- Thermal processes can mimic a power law if the spatial properties
of the emitting medium vary in a suitable way
(84). This particular
slope arises if we consider bremsstrahlung from a spherical
distribution of gas with density
n
 r-3/2 (corresponding to
free-fall) and T
r-3/2 (corresponding to
free-fall) and T  Tvirial
Tvirial
 r-1.
r-1.
- Relativistic particles may be steadily injected with a high Lorentz
factor and then lose energy by synchrotron or inverse Compton emission
before escaping, yielding nonthermal radiation with
L(
 )
)

 -1/2.
-1/2.
- Relativistic particles could be accelerated with an
E-2 differential
spectrum. An (over) simple theory of shock acceleration
(9,
48)
actually yields this law for a compression factor of 4 (the value
expected for a strong nonrelativistic shock).
- Comptonization of injected soft photons yields a power law, which
would have the particular value -½ for a value of the parameter
y = (kT / me c2)
 T2 that is
slightly geometry dependent but typically close to unity.
T2 that is
slightly geometry dependent but typically close to unity.
It is true that theoretical arguments can rule out some of these
emission processes in some particular instances: for example,
bremsstrahlung can never generate a high luminosity
(L  LE) without
LE) without
 T being so large
Comptonization reshapes the spectrum
(71). These
examples of mechanisms, any or all of which could be occurring within
a single source, nevertheless highlight the necessity of other
indicators (such as polarization or spectral breaks) for
discriminating between them.
T being so large
Comptonization reshapes the spectrum
(71). These
examples of mechanisms, any or all of which could be occurring within
a single source, nevertheless highlight the necessity of other
indicators (such as polarization or spectral breaks) for
discriminating between them.
Obviously the values of M and
 are crucial in determining the
properties of an accreting hole; the angular momentum parameter
(J / Jmax) is also important. We conclude
further, and somewhat less trivially, that it is the value of
are crucial in determining the
properties of an accreting hole; the angular momentum parameter
(J / Jmax) is also important. We conclude
further, and somewhat less trivially, that it is the value of
 =
=
 /
/
 E
that determines the nature
of the inflow. The value of M itself only enters explicitly (and with
weak fractional powers) when reabsorption effects are important. This
means that there is a genuine physical similarity, not merely a crude
resemblance, between active galactic nuclei and the stellar-scale
phenomena (X-ray binaries, etc.) observed within our own Galaxy.
E
that determines the nature
of the inflow. The value of M itself only enters explicitly (and with
weak fractional powers) when reabsorption effects are important. This
means that there is a genuine physical similarity, not merely a crude
resemblance, between active galactic nuclei and the stellar-scale
phenomena (X-ray binaries, etc.) observed within our own Galaxy.
While it is perhaps foolhardy to put forward any fully comprehensive
unified scheme for the various kinds of AGNs, there have been several
proposals to relate particular categories of objects, or particular
features in their spectra, to specific mechanisms.
7.2. Ordinary QSOs
Most QSOs are radio-quiet and are neither violently variable nor
highly polarized. The main bolometric luminosity, in the
near-ultraviolet, could come from the photosphere of a
radiation-supported torus around a (107 - 108)
M hole. Blandford (24)
has suggested that the characteristic surface temperature is
determined by He recombination, which changes the mean molecular
weight. An isentropic torus of the type discussed in
Section 5.3 would
need to have a very high central density (and a correspondingly low
value of
hole. Blandford (24)
has suggested that the characteristic surface temperature is
determined by He recombination, which changes the mean molecular
weight. An isentropic torus of the type discussed in
Section 5.3 would
need to have a very high central density (and a correspondingly low
value of  in order to be
sufficiently optically thick to thermalize
radiation out at the putative photosphere - indeed, its central
pressure and temperature might have to be so high that nuclear energy
released via hydrogen-burning
(16)
dominates accretion-generated power
(see Figure 4).
in order to be
sufficiently optically thick to thermalize
radiation out at the putative photosphere - indeed, its central
pressure and temperature might have to be so high that nuclear energy
released via hydrogen-burning
(16)
dominates accretion-generated power
(see Figure 4).
Even if one accepts that there is something special about a
photospheric temperature
T = 20, 000 K, the configuration need not
resemble a stable torus. A more tentative and less controversial
conjecture would simply be that typical QSOs are objects where the
central hole is smothered by plasma clouds at distances
(102 - 103)rg,
which are dense enough to be close to LTE [but which are not
necessarily supported quasi-statically by an
n  r-3 density
distribution (cf. Equation 29) at smaller r]. Such a hypothesis would
suffice to explain the "UV bump" in quasar spectra
(78,
79). The
filaments emitting the broad spectral lines would lie outside this
photosphere. Realistically, one expects an additional nonthermal
component due to shocks and/or magnetic flaring (by analogy with O
star photospheres, except that in AGNs the escape velocity, and
probably also the characteristic Alfv'en speed, would be very much
higher). The X rays could be attributed to this component, since in
such a model no radiation would escape directly from
r
r-3 density
distribution (cf. Equation 29) at smaller r]. Such a hypothesis would
suffice to explain the "UV bump" in quasar spectra
(78,
79). The
filaments emitting the broad spectral lines would lie outside this
photosphere. Realistically, one expects an additional nonthermal
component due to shocks and/or magnetic flaring (by analogy with O
star photospheres, except that in AGNs the escape velocity, and
probably also the characteristic Alfv'en speed, would be very much
higher). The X rays could be attributed to this component, since in
such a model no radiation would escape directly from
r  rg.
rg.
7.3. Radio Galaxies
In radio galaxies, the direct radiative output from the nucleus is
typically ~ 1042 erg s-1, less than the inferred
output of the beams
that fuel the extended radio components. The energy carried by the
beams in Cygnus A exceeds the central luminosity by a factor
of ~ 10 .
These objects must therefore channel most of their power output
into directed kinetic energy. Moreover, the mass involved in producing
the large-scale radio structure must be large - certainly
> 107
M . The
thermal output from these AGNs is therefore
. The
thermal output from these AGNs is therefore
 10-3LE, implying
that they cannot involve radiation-supported tori; nor can radiation
pressure be important for accelerating the jet material. Such
considerations suggest that strong radio sources may involve massive
spinning black holes onto which matter is accreting very slowly (maybe
10-3
M
10-3LE, implying
that they cannot involve radiation-supported tori; nor can radiation
pressure be important for accelerating the jet material. Such
considerations suggest that strong radio sources may involve massive
spinning black holes onto which matter is accreting very slowly (maybe
10-3
M yr-1) to maintain an ion-supported torus, so
that the holes'
energy is now being tapped electromagnetically and being transformed
into directed relativistic outflow
(108).
yr-1) to maintain an ion-supported torus, so
that the holes'
energy is now being tapped electromagnetically and being transformed
into directed relativistic outflow
(108).
7.4. Radio Quasars and Optically Violent Variables
(OVVs)
Data on OVVs (also known as "blazars") have been reviewed by Angel &
Stockman
(6; see also
87,
88).
For the extreme members of the class,
such as OJ 287 and AO 0235 + 164, the case for beaming seems
compelling. The less luminous objects might also be beamed, but they
could alternatively involve unbeamed synchrotron emission from
r  10rg.
More evidence on the hard X-ray spectrum of such objects would
help to decide between these options. If gamma rays were emitted and
(9.) were fulfilled, the resultant "false photosphere" of
electron-positron pairs would scatter the optical photons and destroy
any intrinsic high polarization
(58).
One would then be disposed to
invoke relativistic beaming, which would increase the intrinsic source
sizes compatible with the observed variability and reduce the
luminosity in the moving frame; this would mean that (9.) was no
longer fulfilled, and gamma rays could escape without being
transformed into pairs.
10rg.
More evidence on the hard X-ray spectrum of such objects would
help to decide between these options. If gamma rays were emitted and
(9.) were fulfilled, the resultant "false photosphere" of
electron-positron pairs would scatter the optical photons and destroy
any intrinsic high polarization
(58).
One would then be disposed to
invoke relativistic beaming, which would increase the intrinsic source
sizes compatible with the observed variability and reduce the
luminosity in the moving frame; this would mean that (9.) was no
longer fulfilled, and gamma rays could escape without being
transformed into pairs.
7.5. Hard X-Ray and Gamma-Ray Sources
Boldt & Leiter
(30,
68)
have proposed a scheme whereby the output in
gamma rays relative to X rays increases as
 decreases. Low-redshift
objects are postulated to have low
decreases. Low-redshift
objects are postulated to have low
 and to emit gamma rays; their
high-z counterparts, however, are fueled at a higher rate, and they
yield most of the X-ray background without contributing
proportionately to the gamma-ray background.
and to emit gamma rays; their
high-z counterparts, however, are fueled at a higher rate, and they
yield most of the X-ray background without contributing
proportionately to the gamma-ray background.
According to White et al.
(128),
the characteristic X-ray spectrums
of active nuclei depends on whether their primary luminosity in hard
photons is
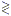 10-2
LE. For a source size of
~ 10rg, this determines
whether or not a pair photosphere is produced (9.). In sources with
high L / r, where a pair photosphere is produced, the emergent
Comptonized spectrum is softer. A small-scale analogue of this
phenomenon may be the galactic compact source Cygnus X-1, which
undergoes transitions between "high" and "low" states, the spectrum
being softer for the former. The fact that many AGNs emit variable X
rays with a flat spectrum (energy index 0.6;
89,
131) suggests that
e+-e- production is inevitable, and that the effects of pairs on
dynamics (99)
and radiative transfer
(130) need further
attention.
10-2
LE. For a source size of
~ 10rg, this determines
whether or not a pair photosphere is produced (9.). In sources with
high L / r, where a pair photosphere is produced, the emergent
Comptonized spectrum is softer. A small-scale analogue of this
phenomenon may be the galactic compact source Cygnus X-1, which
undergoes transitions between "high" and "low" states, the spectrum
being softer for the former. The fact that many AGNs emit variable X
rays with a flat spectrum (energy index 0.6;
89,
131) suggests that
e+-e- production is inevitable, and that the effects of pairs on
dynamics (99)
and radiative transfer
(130) need further
attention.
8. DEMOGRAPHY OF AGNs
Even if AGNs are precursors on the route toward black hole formation
(cf. Figure 1) rather than structures
associated with black holes that
have already formed, it seems hard to escape the conclusion that
massive black holes must exist in profusion as remnants of past
activity; they would be inconspicuous unless infall onto them
recommenced and generated a renewed phase of accretion-powered output
or catalyzed the extraction of latent spin energy.
Estimates of the masses and numbers of "dead" AGNs are bedeviled by
uncertainty about how long individual active objects live and the
evolutionary properties (i.e. the z-dependence) of the AGN population.
As regards the latter, see, for instance,
(81,
114,
127) for recent
reviews of optical data, and
(95,
126) for radio
studies. It has long
been known that the evolution is strong, amounting to a factor of up
to 1000 in comoving density for the strongest sources; the evolution
is differential, being less steep for lower-luminosity objects of all
kinds. It is now feasible to refine these statements, though it is
still premature to be extremely precise about the redshift dependence
of the multivariate function
f (Lrad, Lopt,
LX). And we are still a long
way from having much astrophysical understanding of why the luminosity
function evolves in this way. Anyway, at the epoch z = 2, the
population of strong sources declined on a time scale
tEv  2
× 109 h100 yr;
this is of course an upper limit to the "half-life" of a
particular source, since there may be many generations of objects
within the period tEv.
2
× 109 h100 yr;
this is of course an upper limit to the "half-life" of a
particular source, since there may be many generations of objects
within the period tEv.
Soltan (120)
has given an argument that bypasses the uncertainty in
AGN lifetimes but nevertheless yields useful constraints on the masses
involved in such phenomena and the kinds of galaxies in which they can
reside. The overall energy budget for AGNs is dominated by QSOs (most
of which are "radio quiet"); they contribute an integrated background
luminosity amounting to
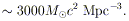
| (35)
|
This estimate involves an uncertain bolometric correction; the
main measured contribution to
 L(
L( ) is typically at
~ 1015 Hz (i.e. in
the ultraviolet). Although some individual quasars could emit more
power in (for instance) the far-ultraviolet, hard X-rays, or gamma
rays, we know enough about the isotropic background in these bands to
be sure that such emission cannot permit a huge bolometric correction
for the typical quasar. The main contribution to (35.) comes from
quasars with
19 < B < 21 (corresponding to bolometric luminosities of
1045 - 1046 h100-2
erg s-1 if they are typically at
z
) is typically at
~ 1015 Hz (i.e. in
the ultraviolet). Although some individual quasars could emit more
power in (for instance) the far-ultraviolet, hard X-rays, or gamma
rays, we know enough about the isotropic background in these bands to
be sure that such emission cannot permit a huge bolometric correction
for the typical quasar. The main contribution to (35.) comes from
quasars with
19 < B < 21 (corresponding to bolometric luminosities of
1045 - 1046 h100-2
erg s-1 if they are typically at
z  2); the counts
flatten off at fainter magnitudes, so (35.) is unlikely to be a severe
underestimate. The energy output from radio galaxies and other
manifestations of active nuclei is much smaller than that from
optically selected quasars; we are therefore probably justified in
using (35.) in the discussion that follows.
2); the counts
flatten off at fainter magnitudes, so (35.) is unlikely to be a severe
underestimate. The energy output from radio galaxies and other
manifestations of active nuclei is much smaller than that from
optically selected quasars; we are therefore probably justified in
using (35.) in the discussion that follows.
The individual remnant masses can be estimated as
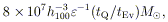
| (36)
|
where  is the overall efficiency with which rest mass is converted
into electromagnetic radiation over a typical quasar's active lifetime
tQ (defined as the time for which the magnitude is
M < - 24). If
quasars were associated with all "bright" galaxies (M < -
21.3), whose
space density is known, the mean hole mass would be
~ 2 × 106 h100-3
is the overall efficiency with which rest mass is converted
into electromagnetic radiation over a typical quasar's active lifetime
tQ (defined as the time for which the magnitude is
M < - 24). If
quasars were associated with all "bright" galaxies (M < -
21.3), whose
space density is known, the mean hole mass would be
~ 2 × 106 h100-3
 -1
M
-1
M .
If only a small fraction of galaxies had ever harbored active nuclei,
the masses (and lifetimes) of each would be correspondingly increased.
.
If only a small fraction of galaxies had ever harbored active nuclei,
the masses (and lifetimes) of each would be correspondingly increased.
The above discussion is important if one wishes to relate nuclear
activity to galactic morphology. However, it is also relevant as a
discriminant between different models
(99).
If individual quasars are
as long lived as is compatible with the cosmological evolution of the
quasar population [i.e.
tQ = tEv in (36.)], their
remnant masses must be as large as
~ 109 h100-3( / 0.1)
M
/ 0.1)
M (the present space density of
remnants being only about that of radio sources with
P178 > 1023
h100-2 W Hz-1 sr-1).
But the luminosity of a "typical" quasar (M
(the present space density of
remnants being only about that of radio sources with
P178 > 1023
h100-2 W Hz-1 sr-1).
But the luminosity of a "typical" quasar (M  - 25.5 for
h100 = ½) corresponds to the Eddington limit for
a mass of "only" ~ 108
M
- 25.5 for
h100 = ½) corresponds to the Eddington limit for
a mass of "only" ~ 108
M ;
so if quasars resemble radiation-supported tori, then they
must have lifetimes such that
(tQ / tEv) << 1, and
individual quasars
must be "switched off" by something internal to the particular system,
rather than being influenced by any change in the overall cosmic
environment (which could occur only on time scales
~ tEv)
(38,
77).
;
so if quasars resemble radiation-supported tori, then they
must have lifetimes such that
(tQ / tEv) << 1, and
individual quasars
must be "switched off" by something internal to the particular system,
rather than being influenced by any change in the overall cosmic
environment (which could occur only on time scales
~ tEv)
(38,
77).
Because of space limitations, I do not speculate here about how
different forms of AGNs might be interrelated. Another contentious
issue is the role of beaming
(25,
28,
32,
113), which has been
advocated to explain compact radio sources (and perhaps also extreme
optical outbursts in OVVs). There is no reason to invoke it, however,
for the typical radio-quiet quasar, and any case it cannot affect the
estimation of (35.). Suffice it to say, as emphasized by Phinney
(99),
that tentative "demographic" studies of imply the following:
- If strong radio sources involve ion-supported tori around holes of
mass
 109
M
109
M , they
could be the "reactivated" remnants of long-lived quasars (with
tQ = tEv).
, they
could be the "reactivated" remnants of long-lived quasars (with
tQ = tEv).
- If quasars radiate at the Eddington limit, then their lifetimes
would be ~ 4 × 107
h(
 /0.1) yr
(cf. Equation 4). Even if their
efficiency
/0.1) yr
(cf. Equation 4). Even if their
efficiency  is high, they must be short lived compared with
tEv. The space density of remnants cannot exceed
10-3
h1002(
is high, they must be short lived compared with
tEv. The space density of remnants cannot exceed
10-3
h1002( /0.1)-1 Mpc-3 unless
their luminosities are highly "super-Eddington."
/0.1)-1 Mpc-3 unless
their luminosities are highly "super-Eddington."
- If Seyfert galaxies are quasar remnants, they cannot be modeled by
radiation-supported tori.
9. SOME CONCLUDING COMMENTS
The foregoing sections have discussed some physical processes and some
idealized models that are relevant to the general phenomenon of active
galactic nuclei. It is, however, depressingly evident how tenuous are
the links between these models and the actual observations. Partly,
this is because the subject is just beginning; but it is also partly
because the observations relate only very indirectly to the primary
energy source - they may instead tell us about secondary reprocessing
that has occurred on much larger scales.
Exhortations and hopes for the future can be summarized in three
categories:
1. On the purely theoretical level, even the simple "toy" models
discussed here need further investigation - they involve effects in
Kerr geometry, collective processes and radiative transfer in
pair-dominated plasma, and acceleration of high gamma particles, none
of which are yet well explored or understood. We need to clarify the
stability of the various axisymmetric configurations: this should
narrow down the embarrassing freedom we now have in specifying the
angular momentum and the enthalpy distribution in tori. Large-scale
computer simulations could be crucial here.
Computer simulations should permit us also to relax the assumption
of stationarity
(59),
which has been implicit in most work on
accretion flows. It may be more realistic to envisage that the feeding
process and the subsequent viscous redistribution of angular momentum
and drainage into the hole are sporadic. There is, after all,
observational evidence for variability on all time
scales. Three-dimensional gas-dynamical codes could also check whether
the Lense-Thirring effect does indeed align the flow in the way simple
arguments suggest. A further valuable computational development will
be the advent of MHD codes able to treat electromagnetic processes
around black holes, as well as the initiation (and possible magnetic
confinement) of relativistic jets.
Detailed computations would also be worthwhile on other classes of
relativistic systems relevant to the evolutionary tracks in
Figure 1
(20).
In particular, supermassive stars with realistic differential
rotation should be investigated. For a suitable angular momentum
distribution, these could acquire a high gravitational binding energy
[cf. the massive disks
(15,
75)
that have been treated analytically].
Redistribution of angular momentum within such objects would be likely
to cause their inner regions to collapse, leaving a massive torus
around the resultant black hole. If too massive, this would be subject
to gravitational instability and could fragment. Otherwise, it would
evolve on a Kelvin or viscous time scale (whichever was shorter). Such
models also remind us that evolution need not be restricted to the
slow time scales of order tE (Equation 4), but that rare
"hypernovae" may Occur.
2. The "peripheral fuzz" at
r >> rg in the emission-line
region and the
radio structures involves physics that is less extreme and more
familiar than that in the central relativistic domain. However, it is
here that one is perhaps more pessimistic about theoretical
progress. This is because in the central region, even though the
physics may be exotic, we have a relatively "clean" problem:
axisymmetric flow in a calculable gravitational field. On the other
hand, in the large-scale sources, environmental effects are plainly
crucial: progress will be slow, for the same reasons that weather
prediction is difficult.
The subject has proceeded in a highly compartmentalized way: the
central engine, the emission-line region, the radio jets, etc., are
modeled somewhat disjointly. To a certain extent this is inevitable -
after all, the relevant scales may differ by many powers of ten. As
data proliferate on source morphology, it no longer seems premature to
develop more comprehensive models, nor to understand the relation of
AGNs to their parent galaxies: If we compare spirals and ellipticals,
are the central masses different? Is the fueling different? What other
environmental influences determine the kind of AGN that is observed?
And do stellar-mass compact objects within our own Galaxy offer many
clues to the mechanisms of AGNs?
3. It is perhaps salutary (especially for relativists) to remain aware
that Einstein's theory is empirically validated only in the weak-field
limit. An extra motive for studying the central region is therefore to
seek a diagnostic (by refining our models for galactic nuclei) that
could test strong-field general relativity and check whether the
space-time around a rotating black hole is indeed described by the
Kerr metric.
Ginzburg (53)
has recently remarked on how surprisingly slowly most
sciences develop. Concentrated activity over a short time-base may
give the illusion that progress is fast, but the advance of science -
particularly where data are sparse - displays a slowly rising trend,
with large-amplitude "sawtooth" fluctuations superposed on it as
fashions come and go. There has been progress toward a consensus, in
that some bizarre ideas that could be seriously discussed a decade ago
have been generally discarded. But if we compare present ideas with
the most insightful proposals advanced when quasars were first
discovered 20 years ago (such proposals being selected, of course,
with benefit of hindsight), progress indeed seems meager. It is
especially instructive to read Zeldovich & Novikov's (1964) paper
entitled "The Mass of Quasi-Stellar Objects"
(133).
In this paper, on
the basis of early data on 3C 273, they conjectured the following:
(a)
Radiation pressure perhaps balances gravity, so the central mass is
~ 108
M . (b) For a likely efficiency of 10%, the
accretion rate would be
3M
. (b) For a likely efficiency of 10%, the
accretion rate would be
3M yr-1. (c) The radiation would come from an effective
"photosphere" at a radius ~ 2 × 1015 cm (i.e.
>> rg), outside of which
line opacity would cause radiation to drive a wind. (d) The accretion
may be self-regulatory, with a characteristic time scale of ~ 3
yr. These suggestions accord with the ideas that remain popular today,
and we cannot yet make many firmly based statements that are more
specific.
yr-1. (c) The radiation would come from an effective
"photosphere" at a radius ~ 2 × 1015 cm (i.e.
>> rg), outside of which
line opacity would cause radiation to drive a wind. (d) The accretion
may be self-regulatory, with a characteristic time scale of ~ 3
yr. These suggestions accord with the ideas that remain popular today,
and we cannot yet make many firmly based statements that are more
specific.
ACKNOWLEDGMENTS
I am grateful for discussions and collaboration with many colleagues,
especially M.C. Begelman, R.D. Blandford, A.C. Fabian, and E.S.
Phinney.
REFERENCES
- Abramowicz, M., Calvani, M., Nobili, L.
1980. Ap. J. 242: 772
- Abramowicz, M., Jaroszynski, M., Sikora, M.
1978. Astron. Astrophys. 63: 221
- Abramowicz, M.A., Lasota, J.P.
1980. Acta Astron. 30: 35
- Abramowicz, M., Piran, T.
1980. Ap. J. Lett. 241: L7
- Abramowicz, M.A., Sharp, N.A.
1983. Astrophys. Space Sci. 96: 431
- Angel, R., Stockman, H.S.
1980. Ann. Rev. Astron. Astrophys. 18: 321
- Araki, S., Lightman, A.P.
1983. Ap. J. 269: 49
- Arons, J.
1979. Space Sci. Rev. 24: 437
- Axford, W.I.
1981. Proc. Tex. Symp., 10th, Ann. NY Acad. Sci. 375:
297
- Balick, B., Heckman, T.M.
1982. Ann. Rev. Astron. Astrophys. 20: 431
- Bardeen, J.M.
1970. Nature 226: 64
- Bardeen, J.M. 1973.
In Les Astres Occlus, ed. C. DeWitt, B.S.
DeWitt, p. 219. New York: Gordon & Breach
- Bardeen, J.M., Petterson, J.A.
1975. Ap. J. Lett. 195: L65
- Bardeen, J., Press, W., Teukolsky, S.
1972. Ap. J. 178: 347
- Bardeen, J.M., Wagoner, R.V.
1971. Ap. J. 167: 359
- Begelman, M.C.
1984. Proc. IAU Symp. 112, Very-Long-Baseline
interferometry, ed. R. Fanti, K. Kellermann, G. Setti. In press
- Begelman, M.C., Blandford, R.D., Rees, M.J.
1984. Rev. Mod. Phys. 56: 255
- Begelman, M.C., McKee, C.F.
1983. Ap. J. 271: 89
- Begelman, M.C., McKee, C.F., Shields, G.A.
1983. Ap. J. 271: 70
- Begelman, M.C., Rees, M.J.
1978. M.N.R.A.S. 185: 847
- Begelman, M.C., Rees, M.J.
1984. M.N.R.A.S. 206: 209
- Bistnovatyii-Kogan, G.S., Zeldovich, Y.B., Sunyaev,
R.A.
1971. Sov. Astron. AJ 15: 17
- Blandford, R.D.
1976. M.N.R.A.S. 176: 465
- Blandford, R.D.
1984. In Numerical Astrophysics, ed. J. Centrella,
R. Bowers, J. LeBlanc. In press
- Blandford, R.D., Konigl, A.
1979. Ap. J. 232: 34
- Blandford, R.D , Payne, D.G.
1982. M.N.R.A.S. 199: 883
- Blandford, R.D., Rees, M.J.
1974. M.N.R.A.S. 169: 395
- Blandford, R.D., Rees, M.J.
1978. Pittsburgh Conf. BL Lac Obj., ed.
A.M. Wolfe, p. 328. Pittsburgh: Univ. Pittsburgh Press
- Blandford, R.D., Znajek, R.L.
1977. M.N.R.A.S. 179: 433
- Boldt, E., Leiter, D.
1984. Ap. J. 276: 427
- Bonometto, S., Rees, M.J.
1971. M.N.R.A.S. 152: 21
- Browne, I.W.A., Orr, M.J.L., Davis, R.J., Foley, A.,
Muxlow, T. W.B., Thomasson, P.
1982. M.N.R.A.S. 198: 673
- Burbidge, G.R., Burbidge, E.M., Sandage, A.
1963. Rev. Mod. Phys. 35: 947
- Burns, M.L., Lovelace, R.V.E.
1982. Ap. J. 262: 87
- Callahan, P.S.
1977. Astron. Astrophys. 59: 127
- Carter, B. 1979. In
Active Galactic Nuclei, ed. C. Hazard, S.
Mitton, p. 273. Cambridge: Cambridge Univ. Press
- Carter, B. 1979. In
General Relativity, ed. S.W. Hawking, W.
Israel, p. 294. Cambridge: Cambridge Univ. Press
- Cavaliere, A., Giallongo, E., Messina, A., Vagentti,
F.
1983. Ap. J. 269: 57
- Cavaliere, A., Morrison, P.
1980. Ap. J. Lett. 238: L63
- Cavallo, G., Rees, M.J.
1978. M.N.R.A.S. 183: 359
- Christodoulou, D.
1970. Phys. Rev. Lett. 25: 1596
- Colpi, M., Maraschi, L., Treves, A.
1984. Ap. J. In press
- Condon, J.J., Condon, M.A., Mitchell, K.J., Usher,
P.D.
1980. Ap. J. 242: 486
- Coroniti, F.V.
1981. Ap. J. 244: 587
- Cowie, L.L., Ostriker, J.P., Stark, A.A.
1978. Ap. J. 226: 1041
- Dahlbacka, G.H., Chapline, G.F., Weaver, T.A.
1974. Nature 250: 37
- Damour, T.
1975. Ann. NY Acad. Sci. 262: 113
- Drury, L.O'C.
1983. Rep. Prog. Phys. 46: 973
- Eardley, D.M., Lightman, A.P.
1975. Ap. J. 200: 187
- Fishbone, L.G., Moncrief, V.
1976. Ap. J. 207:962
- Flammang, R.A.
1982. M.N.R.A.S. 199: 833
- Frank, J.
1979. M.N.R.A.S. 187: 883
- Ginzburg, V.L.
1983. Waynflete Lectures on Physics. Oxford: Pergamon
- Gould, R.J.
1981. Phys. Fluids 24: 102
- Gould, R.J.
1982. Ap. J. 254: 755
- Gould. R.J.
1982. Ap. J. 263: 879
- Guilbert, P.W.
1981. M.N.R.A.S. 197: 451
- Guilbert, P.W., Fabian, A.C., Rees, M.J.
1983. M.N.R.A.S. 205: 593
- Hawley, J., Smarr, L.L. 1984. In
Numerical Astrophysics, ed. J.
Centrella, R. Bowers, J. LeBlanc. In press
- Hills, J.G.
1975. Nature 254: 295
- Hills, J.G.
1978. M.N.R.A.S. 182: 517
- Hutchings, J.B., Campbell, B.
1983. Nature 303: 584
- Jaroszynski, M., Abramowicz, M.A., Paczynski, B.
1980. Acta Astron. 30: 1
- Kafatos, M., Leiter, D.
1979. Ap. J. 229: 46
- Kozlowski, M., Jaroszynski, M., Abramowicz, M.A.
1978. Astron. Astrophys. 63: 209
- Kandrup, H.
1982. Ap. J. 255: 691
- Katz, J.I.
1976. Ap. J. 206: 910
- Leiter, D., Boldt, E.
1982. Ap. J. 260: 1
- Lightman, A.P.
1982. Ap. J. 253: 842
- Lightman, A.P., Band, D.L.
1981. Ap. J. 251: 713
- Lightman, A.P., Giacconi, R., Tananbaum, H.
1978. Ap. J. 224: 375
- Lovelace, R.V.E.
1976. Nature 262: 649
- Lynden-Bell, D.
1969. Nature 223: 690
- Lynden-Bell, D.
1978. Phys. Scr. 17: 185
- Lynden-Bell, D., Pineault, S.
1978. M.N.R.A.S. 185: 679
- Macdonald, D., Thorne, K.S.
1982. M.N.R.A.S. 198: 345
- MacMillan, S.L.W., Lightman, A.P., Cohn, H.
1981. Ap. J. 251: 436
- Malkan, M.A.
1983. Ap. J. 268: 582
- Malkan, M.A., Sargent, W.L.W.
1982. Ap. J. 254: 22
- Maraschi, L., Roasio, R., Treves, A.
1982. Ap. J. 253: 312
- Marshall, H.L., Avni, Y., Tananbaum, H., Zamorani,
G.
1983. Ap. J. 269: 35
- Matthews, W.G.
1983. Ap. J. 272: 390
- Meszaros, P.
1975. Astron. Astrophys. 44: 59
- Meszaros, P.
1983. Ap. J. Lett. 274: L13
- Meszaros, P., Ostriker, J.P.
1984. Ap. J. In press
- Miley, G., Norman, C.
1984. Ap. J. Submitted for publication
- Moore, R.L., Stockman, H.S.
1981. Ap. J. 243: 60
- Moore, R.L., Stockman, H.S.
1984. Ap. J. In press
- Mushotzky, R.F. 1984.
Proc. Tex. Symp. Relativ. Astrophys., 11th. In press
- Narayan, R., Nityananda, R., Wiita, P.
1983. M.N.R.A.S. 205: 1103
- Ostriker, J.P.
1983. Ap. J. 273: 99
- Ostriker, J.P., McCray, R., Weaver, R., Yahil, A.
1976. Ap. J. Lett. 208: L61
- Paczynski, B., Abramowicz, M.A.
1982. Ap. J. 253: 897
- Papaloizou, J.C.B., Pringle, J.E.
1984. M.N.R.A.S. In press
- Peacock, J.A., Gull, S.F.
1981. M.N.R.A.S. 196: 611
- Penrose, R.
1969. Riv. Nuovo Cimento 1: 252
- Phinney, E.S.
1982. M.N.R.A.S. 198: 1109
- Phinney, E.S. 1983. In
Astrophysical Jets, ed. A. Ferrari, A.G.
Pacholczyk, p. 201. Dordrecht: Reidel
- Phinney, E.S.
1983. PhD thesis. Univ. Cambridge, Engl.
- Piran, T., Shaham, J.
1977. Ap. J. 214: 268
- Pringle, J.E.
1981. Ann. Rev. Astron. Astrophys. 19: 137
- Pudritz, R.
1981. M.N.R.A.S. 195: 881
- Pudritz, R., Fahlman, G.C.
1982. M.N.R.A.S. 198: 689
- Ramaty, R., Meszaros, p.
1981. Ap. J. 250: 384
- Rees, M.J.
1978. Nature 275: 516
- Rees, M.J.
1978. Observatory 98: 210
- Rees, M.J. 1984.
Proc. IAU Symp. 112, Very-Long-Baseline
Interferometry, ed. R. Fanti, K. Kellermann, G. setti. In press
- Rees, M.J., Begelman, M.C., Blandford, R.D.,
Phinney, E.S.
1982. Nature 295: 17
- Robinson, I., Schild, A., Schucking, E., eds.
1964. Proc. Tex.
Conf. Relativ. Astrophys., 1st. Chicago: Univ. Chicago Press
- Rosner, R. 1984. Preprint
- Sakimoto, P.J., Coroniti, F.V.
1981. Ap. J. 247: 19
- Salpeter, E.E.
1964. Ap. J. 140: 796
- Scheuer, P.A.G., Readhead, A.C.S.
1979. Nature 277: 182
- Schmidt, M., Green, R.F.
1983. Ap. J. 269: 352
- Seguin, F.G.
1975. Ap. J. 197: 745
- Shakura, N.I., Sunyaev, R.A.
1973. Astron. Astrophys. 24: 337
- Shakura, N.I., Sunyaev, R.A.
1976. M.N.R.A.S. 175: 613
- Sikora, M.
1981. M.N.R.A.S. 196: 257
- Sikora, M., Wilson, D.B.
1981. M.N.R.A.S. 197: 529
- Soltan, A.
1982. M.N.R.A.S. 200: 115
- Stepney, S.
1983. M.N.R.A.S. 202: 467
- Svensson, R.
1982. Ap. J. 258: 131
- Svensson, R.
1982. Ap. J. 258: 335
- Svensson, R.
1984. M.N.R.A.S. In press
- Takahara, F., Tsuruta, S.
1982. Prog. Theor. Phys. 67: 485
- Van der Laan, H., Windhorst, R.A. 1983. In
Astrophysical Cosmology,
ed. H. Bruck, G. Coyne, M. Longair, p. 349. Vatican City: Vatican Publ.
- Veron, P.
1983. Proc. Liege Symp. Quasars Gravitational Lenses.
Liege: Obs. Publ.
- White, N.E., Fabian, A.C., Mushotzky, R.F.
1984. Astron. Astrophys. In press
- Witta, P.
1982. Ap. J. 256: 666
- Wilson, D.B.
1982. M.N.R.A.S. 200: 881
- Worrall, D.M., Marshall, F.E.
1984. Ap. J. 276: 434
- Zdiarski, A.A.
1982. Astron. Astrophys. 110: L7
- Zeldovich, Y.B., Novikov, I.D.
1964. Dokl. Acad. Nauk. SSSR 158: 811
- Znajek, R.L.
1977. M.N.R.A.S. 179: 457
 INTRODUCTION
INTRODUCTION
 INFERENCES INSENSITIVE TO DETAILED MODEL
INFERENCES INSENSITIVE TO DETAILED MODEL
 Some Fiducial Numbers
Some Fiducial Numbers
 Processes in Ultrahot Thermal Plasma
Processes in Ultrahot Thermal Plasma
 Cyclotron/Synchrotron and Inverse Compton Cooling
Cyclotron/Synchrotron and Inverse Compton Cooling
 RADIAL ACCRETION FLOWS
RADIAL ACCRETION FLOWS
 Spherical Accretion
Spherical Accretion
 BLACK HOLES ACCORDING TO GENERAL RELATIVITY
BLACK HOLES ACCORDING TO GENERAL RELATIVITY
 The Kerr Metric
The Kerr Metric
 Three Astrophysically Important Relativistic
Effects
Three Astrophysically Important Relativistic
Effects
 ACCRETION FLOWS WITH ANGULAR MOMENTUM
ACCRETION FLOWS WITH ANGULAR MOMENTUM
 Origin of Infalling Matter
Origin of Infalling Matter
 Thin Disks
Thin Disks
 General Structure of Tori or Thick Disks
General Structure of Tori or Thick Disks
 RADIATION-SUPPORTED TORI
RADIATION-SUPPORTED TORI
 Ion-Supported Tori
Ion-Supported Tori
 JET FORMATION
JET FORMATION
 SOME COMMENTS ON PHENOMENOLOGY
SOME COMMENTS ON PHENOMENOLOGY
 The Continuum Spectrum
The Continuum Spectrum
 Ordinary QSOs
Ordinary QSOs
 Radio Galaxies
Radio Galaxies
 Radio Quasars and Optically Violent Variables
(OVVs)
Radio Quasars and Optically Violent Variables
(OVVs)
 Hard X-Ray and Gamma-Ray Sources
Hard X-Ray and Gamma-Ray Sources
 DEMOGRAPHY OF AGNs
DEMOGRAPHY OF AGNs
 SOME CONCLUDING COMMENTS
SOME CONCLUDING COMMENTS
 REFERENCES
REFERENCES

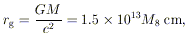
 . The
characteristic minimum time scale for variability is
. The
characteristic minimum time scale for variability is
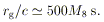
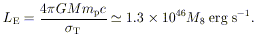
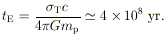
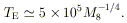
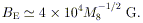
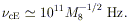
 e (equivalent to
the synchrotron lifetime in the field BE) is
e (equivalent to
the synchrotron lifetime in the field BE) is
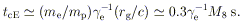
 >. If a
luminosity
f LE emerges in photons with
h
>. If a
luminosity
f LE emerges in photons with
h me
c2, which can
interact (with a cross section
~
me
c2, which can
interact (with a cross section
~  T) to produce
electron-positron pairs
(
T) to produce
electron-positron pairs
(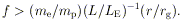
 LE is
generated within radii a few times rg:
LE is
generated within radii a few times rg:
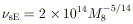
 1 Mev, then
electron-positron pairs would inevitably be produced.
1 Mev, then
electron-positron pairs would inevitably be produced.
 1 Mev even if the
ions are much hotter. Detailed
discussions of these various time scales are given by Gould
(
1 Mev even if the
ions are much hotter. Detailed
discussions of these various time scales are given by Gould
(
 T > 1) source,
then the emergent spectrum depends
essentially on the parameter
y =
T > 1) source,
then the emergent spectrum depends
essentially on the parameter
y = 
 (Te)
into the temperature range where pair
production is important, one must specify the column density
nir of
the source as a second parameter (ni being the ion
density). When
nir << 1, the dominant pair production is via
e-p collisions; but for
sources of higher column density, relation (9) may be fulfilled, and
more pairs come from
(Te)
into the temperature range where pair
production is important, one must specify the column density
nir of
the source as a second parameter (ni being the ion
density). When
nir << 1, the dominant pair production is via
e-p collisions; but for
sources of higher column density, relation (9) may be fulfilled, and
more pairs come from
 f(me /
mp) q-1(kTe /
me c2)-1/2,
which is << 1 for a plasma with
kTi
f(me /
mp) q-1(kTe /
me c2)-1/2,
which is << 1 for a plasma with
kTi 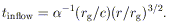
 provides the power, the
value of
provides the power, the
value of  needed to supply a luminosity L can be written as
needed to supply a luminosity L can be written as

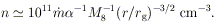
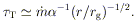
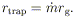
 ,
,
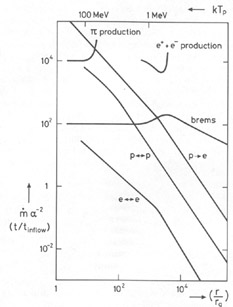
 production. The proton temperature is taken as the virial temperature
[kT = mp c2(r /
rg)-1], but the electron
temperature is assumed to vary as
r-1/2 when the electrons are relativistic. The diagram
shows that for free-fall accretion at the "critical" rate
(
production. The proton temperature is taken as the virial temperature
[kT = mp c2(r /
rg)-1], but the electron
temperature is assumed to vary as
r-1/2 when the electrons are relativistic. The diagram
shows that for free-fall accretion at the "critical" rate
(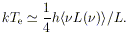
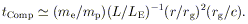
 kTvirial =
mp c2(r /
rg)-1 .
If Te < Tvirial, then the inflow
must be supersonic, with the
pressure support unimportant. Conversely, if there is a range of r
where tComp < tinflow but
Te > Tvirial,
steady inflow is impossible: if the
flow were constrained to remain spherically symmetrical, "limit cycle"
behavior would develop; but in more general geometry, inflow in some
directions could coexist with out-flow in others
(
kTvirial =
mp c2(r /
rg)-1 .
If Te < Tvirial, then the inflow
must be supersonic, with the
pressure support unimportant. Conversely, if there is a range of r
where tComp < tinflow but
Te > Tvirial,
steady inflow is impossible: if the
flow were constrained to remain spherically symmetrical, "limit cycle"
behavior would develop; but in more general geometry, inflow in some
directions could coexist with out-flow in others
( direction. This critical
surface, with equatorial radius
direction. This critical
surface, with equatorial radius
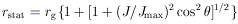
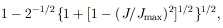
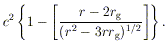
 min =
2
min =
2 3 rg
c. Circular
orbits closer in than this have more angular momentum and are less
tightly bound (as for orbits in classical theory when the effective
force law is
3 rg
c. Circular
orbits closer in than this have more angular momentum and are less
tightly bound (as for orbits in classical theory when the effective
force law is
 r-n,
with n > 3): the orbits have zero
binding energy for
r = 4rg (with corresponding angular momentum
r-n,
with n > 3): the orbits have zero
binding energy for
r = 4rg (with corresponding angular momentum
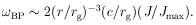
 BP, is less
than the inflow
time, can be axisymmetric with respect to the hole irrespective of the
infalling material's original angular momentum vector. The
Lense-Thirring precession, an inherently relativistic effect, thus
guarantees that a wide class of flow patterns near black holes will be
axisymmetric - an important simplification of the problem.
BP, is less
than the inflow
time, can be axisymmetric with respect to the hole irrespective of the
infalling material's original angular momentum vector. The
Lense-Thirring precession, an inherently relativistic effect, thus
guarantees that a wide class of flow patterns near black holes will be
axisymmetric - an important simplification of the problem.
 with the
horizon. This analogy can be put on a more rigorous
basis (
with the
horizon. This analogy can be put on a more rigorous
basis (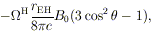
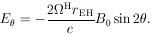
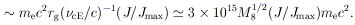
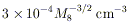
 to the
resistance of the hole ZH:
to the
resistance of the hole ZH:
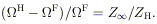
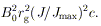
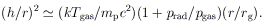
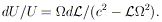
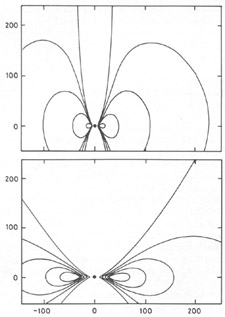
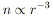
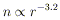
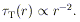
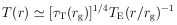
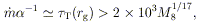
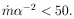
 emits within
this cone a greatly enhanced luminosity
~
emits within
this cone a greatly enhanced luminosity
~