Published in "The Interstellar Medium in Galaxies", eds. Harley A. Thronson, Jr. and J. Michale Shull, 1990

MAGNETIC FIELDS IN GALAXIES

Richard Wielebinski


Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, D-5300 BONN 1, F.R.G.

Introduction. The search for magnetic fields in the Galaxy was started already at the turn of this century, soon after polarization characteristics of the Felspar crystal were discovered. Additional impetus came from the development of polaroid foil which made this observing technique available even to amateur astronomers. The first substantiated discovery is due to Meyer (1920) who measured the polarization of the Hubble's variable nebula NGC2261. This was an observation of the polarization of a galactic source but it showed that magnetic fields exist and play an important role in the universe. At the same time methods of measuring of the solar magnetic field were being developed. Theoretical arguments for the existence of magnetic fields in galaxies were based on the need of confinement of cosmic particles (e.g. Fermi, 1949). The discovery of a magnetic field in an external galaxy is due to Öhman (1942) who used first a Felspar polarimeter and later a Wollaston prism to observe the polarized emission in Andromeda nebula (M31).

The progress in the measurement of magnetic fields in galaxies using optical polarization methods was slow, since the observations were very difficult. It was the discovery of the radio polarization of the synchrotron emission which added a new and important technique for studying magnetic fields. Also the Zeeman effect in HI clouds (and more recently in OH, H2O, CCS sources) added new data on magnetic fields in dense molecular clouds in the Galaxy. The progress in the past ten years was basic in giving us an insight into the morphology of the magnetic fields in galaxies.

Table of Contents

METHODS OF MEASURING MAGNETIC FIELDS

THE MAGNETIC FIELDS IN OUR GALAXY

THE MAGNETIC FIELDS IN GALAXIES

RESULTS FOR SOME INDIVIDUAL GALAXIES

THE MAGNETIC FIELD STRENGTH

THE INTERPRETATION OF MAGNETISM IN GALAXIES

THE SEED FIELD

THE 'FUTURE' OF MAGNETIC FIELDS

REFERENCES

1. METHODS OF MEASURING MAGNETIC FIELDS

The methods of measurement of the magnetic fields are indirect. Essentially the measurement of the optical, infrared or radio polarization (e.g. Sofue et al., 1986; Beck, 1986; Heiles, 1976) gives us the basic data. In the case of optical polarization it is the alignment of dust grains by magnetic fields that gives an observable effect. At radio frequencies linearly polarized waves are generated by relativistic electrons in magnetic fields.

A number of effects are responsible for the polarization of optical light. Light scattered by dust grains (Rayleigh scattering) becomes partially polarized with the orientation of the observed polarization perpendicular to a line pointing to the light source. In the case of dust grains aligned in magnetic fields (the Davis-Greenstein effect) we see in the case of the scattered light the polarization perpendicular to the magnetic field while we see the polarization vectors parallel to the field orientation for the directly transmitted light. There are many open questions in the details of the theory of optical polarization generation (e.g. see Purcell, 1979 and Hildebrand, 1988). To study magnetic fields with optical methods a separation of the various effects is necessary.

At radio frequencies the synchrotron emission is emitted with the E vector perpendicular to the orientation of the magnetic field (e.g. Ginzburg and Syrovatskij, 1969). The observed vectors must be corrected for the Faraday rotation which takes place in the galaxy itself, the intergalactic medium and in our Galaxy. To eliminate the Faraday effect we need to have observations at several frequencies. The Faraday effect itself gives us information about the field component parallel to the line of sight. It is also important to consider the effects of different beams for the different frequencies.

The most direct method of measurement of the magnetic fields is the Zeeman effect. The Zeeman effect was observed in molecular clouds as a frequency shift of the opposite circular polarization signals of such molecules as HI, OH, H2O, CCS etc. Such observations give us information about the magnetic field in the molecular clouds. The magnetic field strength can be inferred from the synchrotron emission intensity (using equipartition arguments).

2. THE MAGNETIC FIELDS IN OUR GALAXY

There are extensive studies of the optical polarization of stars in the Galaxy. The pioneering work of Hiltner (1949) and Hall (1949) was followed by large scale surveys of Behr (1959) and Mathewson and Ford (1970). These data were reanalyzed by Ellis and Axon (1978). The general conclusion is that this method gives us at most information about our local neighborhood. The magnetic field is aligned in general along the galactic plane, but in the direction of l = 45°. Beyond a circle of 600 pc the magnetic field is directed towards l = 70°. This field configuration is attributed to a local bubble or a single loop of a more general field.

The direct mapping of the polarized radio continuum emission gave us insight into the magnetic fields of galactic objects. The early observations by Mayer et al. (1957) were the first to give information about the magnetic field in the Crab Nebula, a supernova remnant. Galactic radio polarization was discovered by Westerhout et al., 1962) and Wielebinski et al., (1962). The surveys of Berkhuijsen and Brouw (1963), Wielebinski and Shakeshaft (1964) and Mathewson and Milne (1965) at 408 MHz show the local fields only. The direction of l = 140° b = 10° is a direction of a unique singularity where we are looking perpendicular to the local magnetic field. Higher frequency surveys (e.g. Spoelstra, 1984; Junkes et al., 1987) show that more distant magnetic fields could be traced at higher radio frequencies.

The studies of Rotation Measures of extragalactic radio sources have given us a some understanding of the large-scale magnetic field of the Galaxy (e.g. Simrad-Normandin et al., 1981). With this method we get information about B|| (field component parallel to line of sight) only. There is a large scale field with numerous 'local' features. The study of RM's should be improved further using a much larger sample of sources. A study of different zones (MacLeod et al., 1988) offers a possibility of understanding some of the details of the magnetic field structure. One of the interesting results from RM studies is that sudden field reversals occur on scales of a few degrees.

Pulsars offer the most direct method of determining of B||. The reason for this is the fact that we can measure both the RM and the Dispersion Measure. From these two pieces of information the value of B|| can be derived. Recent reanalysis of all the available pulsar data by Lyne and Graham Smith (1989) confirmed a magnetic field in the Galaxy of B|| ~ 3µG, directed towards l = 90° (i.e. along the local spiral arm). Sudden field reversals (indicated by high positive and negative adjacent rotation measures) are seen in a number of directions.

The measurements of the Zeeman effect have succeeded in HI clouds (e.g. Verschuur, 1979), in OH molecular clouds (e.g. Crutcher et al., 1987) and more recently in H2O sources (Fiebig & Güsten, 1989). All the Zeeman measurements, maybe the most direct magnetic field determinations, can be made only in a small number of sources. The fields that have been measured are B > 10 µG, with values of ~ 100µG in some objects. In H2O maser regions magnetic field values are in the milligauss range.

All the data discussed so far gives us the picture that the magnetic fields in the disc of the Galaxy is azimuthal. A recent analysis of Vallee (1988) shows that any deviations of pitch angle of the magnetic field, from the spiral arm are slight, possibly less then 6°. Vallée also deduced a field reversal in the Sagittarius arm. This could support the analysis of Sofue and Fujimoto (1983) who claimed that the magnetic field of the Galaxy is bisymmetric.

The field in the center of our Galaxy is in the Z-direction. The earlier lambda 2.8cm observations (Seiradakis et al., 1985) have been substantiated by new lambda 9 mm observations (Reich, 1989). The magnetic field in the central nucleus area runs perpendicular to the galactic plane, which may be a part of a more extended poloidal field. This non-thermal emission has also an anomalous (positive), spectral index (Reich et al., 1988).

A model of the magnetic field in the Galaxy is shown in figure 1. The fields in the disc have a uniform component Bu and a turbulent component Br. Since Bu|| (from pulsar rotation measures) is ~ 3µG, we can expect Bu ~ 5µG. Since Bu ~ Br the total magnetic field in the plane could have the value of Bt ~ 7µG or more.

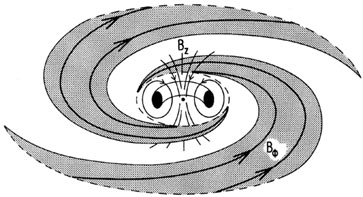
Figure 1

Figure 1. A model of the magnetic field in the Galaxy.

3. THE MAGNETIC FIELDS IN GALAXIES

As mentioned already it was the optical polarization observations that gave us the first information about magnetic fields in external galaxies. Öhman (1942) gave us in addition to the results for M31 the detailed description of all the many problems of the observing technique. The advantages and/or the problems of surface polarimetry compared to the observations of discrete sources (stars, globular clusters) were discussed. The interpretation for the reasons for polarized light had to wait until Davis and Greenstein (1951). The optical polarization studies of galaxies (e.g. Hiltner, 1958; Elvius & Hall, 1965; Appenzeller, 1967; Bingham et al., 1976; Scarrott et al., 1977; Elvius, 1978; Martin & Shawl, 1982; Scarrott et al., 1987) are characterized by ever increasing sensitivity. The photomultiplier has been replaced by a CCD detector. The polarization analyzer remained essentially the same;- polarization foil or a Wollaston prism. Savart plates are also used for studies of stars. A new era of optical polarization observations seems to be at hand in view of the relative availability of medium sized telescopes and sensitive CCD detectors.

The radio observations needed some time to develop sensitive methods to measure polarization in galaxies. The first published result for a galaxy was for M51 by Mathewson et al. (1972) using the then commissioned Westerbork synthesis radio telescope. A follow-up observation of Segalovitz et al. (1976) gave us information about M51 and M81. The Effelsberg 100-m dish has been intensively dedicated to the study of magnetic fields in galaxies since the first results on M31 were published by Beck et al., (1978, 1980). Since that time practically all the large northern galaxies have been mapped in Effelsberg at wavelengths lambda lambda 11 to 2.8 cm. In the quest of angular resolution the Very Large Array (VLA) has been used, in particular in the D array mode, at lower frequencies. More recently the Parkes radio telescope has been used for polarization mapping of the Magellanic Clouds (Haynes et al., 1986, 1990) and for large southern galaxies (Harnett et al., 1989, 1990). The present data base needs to be expanded both in respect to angular resolution (without loss of sensitivity) and to higher frequencies. Some progress with existing radio telescopes is possible. Given longer integration times for the C and B array mapping at the VLA we should get better information. The 100-m telescope in Effelsberg with a multibeam receiver at lambda 9mm wavelength will allow 25" angular resolution practically free of Faraday effects. The commissioning of the Australia Telescope should usher in a new era of studies of southern galaxies.

4. RESULTS FOR SOME INDIVIDUAL GALAXIES

In the following I will describe some of the results for individual galaxies. The order of the galaxies is firstly size, but later some of the types will be described collected in groups. The description of the magnetic field structure will follow the ideas developed from the early observations namely that fields are either axisymmetic [ASS] or bisymmetric [BSS] spirals. The analysis of the magnetic fields, which was originally developed by Tosa and Fujimoto (1978), involves the study of the Rotation Measure as a function of azimuthal angle Theta and is illustrated in figure 2. Further details of such studies can be found in Sofue et al. (1985) and Krause et al. (1989a, b).

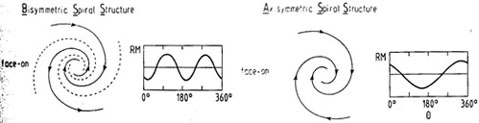
Figure 2

Figure 2. The basic mode configurations. Rotation Measure as a function of Azimuth Theta.

LMC     Optical observations of the Large (and Small) Magellanic Cloud (Schmidt, 1970; Mathewson and Ford, 1970) showed the presence of magnetic fields in both galaxies. The initial interpretation in terms of a 'Pan-Magellanic field' was questioned by Schmidt (1976) who pointed out that the local (foreground) field seems to be also aligned in the LMC-SMC direction. A detailed study of the LMC was recently given by Klein et al. (1989). Radio polarization studies of the LMC (Haynes et al., 1990) show that magnetic fields are seen as a series of filaments originating in 30 Doradus nebula. This in fact agrees with the recent results in HI, CO, FIR, UV etc. These results would suggest that 30 Doradus is the nucleus of the LMC. The filamentary structure of the young components is indeed baffling. These filaments could be spiral arms. This should lead to a reclassification of the LMC to be a 'Spiral' rather then the present classification as 'Irregular'.

SMC     The Small Magellanic Cloud is considered to be the nearest dwarf galaxy. As such the magnetic field structure is of great interest. Optical studies showed some vectors aligned with the 'body' of the SMC, others to be directed towards the LMC (Schmidt 1976). Radio data (Loiseau et al., 1987) shows aligned field in the southern 'body', in agreement with optical data. This indicates a field along the 'body'. However the field is weak, possibly less then 3 µG, as expected in a dwarf galaxy.

M31     This northern spiral has been a subject of extensive study giving possibly the best information of any galaxies to date. The Effelsberg lambda lambda 11 and 6cm data have now been supplemented with multi-field VLA observations at lambda 20cm. The polarized intensity is concentrated to a 'ring' with minima in the direction of the major axis (where Faraday depolarization is expected to be greatest). Due to its inclination the Faraday rotation is strong and can thus be measured with some accuracy. M31 has the prototype 'axisymmetric' spiral field structure (see Beck, 1982 and Beck et al., 1989 and figures 3 and 4). However in detail small wave-like field perturbations are observed.

M33     Multifrequency observations of Buczilowski & Beck, (1987) have now been analyzed in some detail. The field in M33 is possibly 'bisymmetric' but this conclusion is only tentative because of problems of sensitivity in this rather low luminosity galaxy. It is difficult in general to determine Faraday rotation in face-on galaxies, in particular when the magnetic field strength is low. A regular field structure is seen in M33 in the northern spiral arm while in the south considerable perturbations are present.

NGC55     This large irregular galaxy is seen edge-on (e.g. Hummel et al., 1986). In the VLA observations no polarized emission was detected. Recent mapping with the Parkes telescope (Harnett et al., 1990) has shown some weak polarized emission in the nuclear area. This would be the second (after the SMC) dwarf galaxy with a confirmed magnetic field.

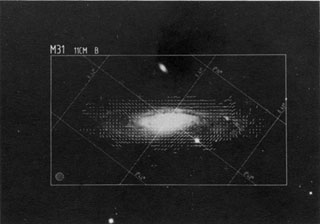
Figure 3

Figure 3. A low resolution map of the magnetic field in M31 (based on Effelsberg data from Beck et al., 1980 with correction for the Faraday rotation in our Galaxy only).

Figure 4

Figure 4. A 'zoom' of a section of M31 with higher angular resolution (VLA data from Beck et al., 1989).

M101     In M101 the giant HII regions, which have NGC designations themselves, dominate the structure. In spite of this the diffuse nonthermal emission shows two polarization maxima on opposite sides of the nucleus (Gräve et al. 1990). Magnetic fields on a grand scale are present also in this galaxy.

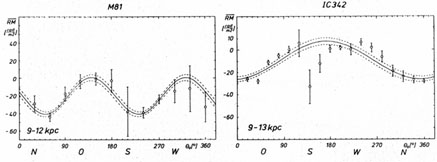
IC342     This galaxy was the subject of detailed studies by Krause et al. (1989a). Both Effelberg and VLA multifrequency data are available. The rotation measure analysis of this galaxy (see figure 5) shows an axisymmetric field. Higher angular resolution observations show that the symmetry on the two opposite sides of the galaxy is quite different. In the South-East a series of very extended filamentary arcs are observed. A polarization maximum in one arc shows zero Faraday rotation with rotation in the same direction on either side. We must be looking into an 'S' like magnetic field filament. In the North-West a very fine filamentary structure is seen with a number of maxima and minima. However the direction of the 'E' vector (i.e. magnetic field) does not change.

M81     This 'grand design' spiral galaxy was subject of multifrequency studies by Krause et al. (1989b). It is the bisymmetric field prototype (see figure 5 and figure 6). However the symmetry is also not perfect. The South-West arm breaks up into two filaments aligned in the direction of the spiral arms. The highest degree of polarization is in the inter-arm region. This is a very significant result pointing to a tangled field in the arms.

Figure 5

Figure 5. Rotation measure studies for M81 and IC342. (from Krause et al., 1989a, b)

NGC4258     This galaxy has posed a problem of interpretation in view of its 'anomalous arms' (van der Kruit et al., 1972). The fact that these anomalous arms are highly polarized (van Albada, 1978, Hummel et al., 1989) implies that magnetic fields are involved in the origin of the radio emission in this object. At low angular resolution the two arms show up as maxima of polarization symmetrically disposed about the nucleus. Rotation measure analysis by Hummel et al. (1989) implies that these arms are in the plane, or nearly in the plane, of the galaxy.

Figure 6

Figure 6. The magnetic field orientation in M81 (Krause et al., 1989b)

NGC6946     This galaxy was one of the earliest to be mapped with polarization information at a high radio frequency (Klein et al., 1982). Subsequent multifrequency observation studies both at the VLA and in Effelsberg (Harnett et al., 1989a) showed that in spite of a regular field structure no decision between axisymmetric of bisymmetric field could be made. The local perturbations in this 'Arp' galaxy make any decision impossible.

M51     There are extensive data for this galaxy both in optical and radio domain. The original Westerbork data (Segalovitz et al., 1976) have been supplemented by Effelsberg and VLA observations. This galaxy was the first to be investigated by Tosa and Fujimoto (1978) for the presence of a bisymmetrical magnetic field. Also excellent optical polarization CCD maps have been made by Scarrott et al. (1987). There is a general agreement between the optical and radio data for most of the galaxy. In the South-West part of the galaxy the optical and radio data disagree (Beck et al., 1988). More recent radio data (Horellou et al., 1990) confirm the BSS magnetic field. The M51 data confirm that the optical and radio polarizations are due to the same magnetic field.

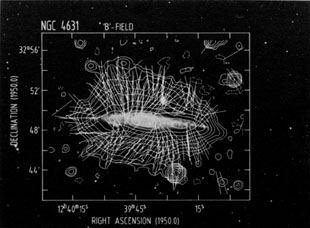
NGC4631     The question of the structure of the magnetic fields above the plane of a galaxy is of great interest. The closure of magnetic field lines is expected to occur in the halo. The classical edge-on galaxy with a thick disc halo is NGC4631 (Ekers & Sancisi, 1977; Wielebinski & von Kap-herr, 1977). The observations of this galaxy with the VLA (Hummel et al. 1988) showed the existence of halo fields. The orientation of the field is normal to the disc (see figure 7) on the assumption of low Faraday rotation. It seems that Parker instabilities or a galactic wind are pushing the magnetic field above the plane of this galaxy. This observation must however be treated with some caution since NGC4631 has the most extended synchrotron halo. The field strength in the halo may be as much as ~ 2 µG.

Figure 7

Figure 7. The 'B'-field orientation in NGC4631. (from Hummel et al., 1989; not corrected for Faraday effect)

NGC891     This nearly perfect edge-on galaxy has been studied in radio continuum (e.g. Allen et al., 1978; Klein et al., 1984). Recent polarization studies by Dahlem, Beck, Hummel, Sukumar, Allen (private communication) indicate a magnetic field away from the plane but not as perpendicular to the plane as in NGC4631. Since data at two frequencies was obtained the confirmation of a low Faraday rotation in the halo (which was so far assumed for NGC4631) has been obtained.

M83     The barred galaxy M83 shows beautiful highly symmetric field structure (Sukumar et al., 1987). More recent VLA observations with higher angular resolution by Sukumar and Allen (1990) indicate that filamentary structure is seen, reminiscent of IC342. It is also interesting to note that the aligned magnetic field starts at the optical edge of M83, where the bar structure stops. In the inner parts of this galaxy the field must be quite turbulent.

NGC253, NGC4945     These large southern galaxies are seen nearly edge-on. Radio continuum observation showed in each galaxy two maxima distributed symmetically about the nucleus (Klein et al., 1983, Harnett et al., 1989). The question if this is only a geometrical effect, or a morphological feature are still open.

NGC3628     This edge-on galaxy show some polarization in the halo (M. Krause, private communication). Again the structure is emphasized by two maxima on opposite sides of the nucleus.

M104     The 'Sombrero' galaxy was known for a long time to have a compact (VLBI) source in the nucleus. Optical polarization studies by Scarrott et al. (1987) showed a field along the disc of this galaxy. The disc emission was finally detected by Bajaja et al. (1999) using the high dynamic mode of the VLA. In addition polarized emission perpendicular to the disc was seen in the nuclear area. Recent analysis of the optical polarization by Matsumura & Seki (1989) suggest also a Z-field in the nucleus superimposed on the azimuthal field in the disc. The rotation curve of M104 (e.g. Wagner et al., 1989) suggests a rotating ring surrounding the nucleus.

M82     This mildly active galaxy is the most studied object in all spectral ranges. Although detailed radio continuum observations were published (e.g. Kronberg et al., 1985) none contained polarization data. Optical polarization (Bingham et al., 1976) is dominated by the light scattered by dust, showing a circular vector distribution. Recent CCD observations of this object, after subtraction of the scattered light component, showed a Z-field in the nuclear area (Neininger, 1989). The radio continuum spectrum of M82 is very well studied (Klein et al., 1988) indicating that the magnetic field may have mean values of ~ 50µG, the highest of any galaxy. A rotating ring which is seen in all constituents (HI, OH, sub-mm continuum, CO etc.) has been interpreted to be instrumental for the production of this Z-field (Lesch et al., 1989).

Many other galaxies have been observed but not in such detail as those mentioned above. For the general scenario we can conclude that magnetic fields are azimuthal in the galaxies except in the nuclear area where fields are in the Z-direction. This is in agreement with the model shown for our Galaxy in figure 1.

5. THE MAGNETIC FIELD STRENGTH

The various methods of observing the magnetic fields described at the beginning of this review gave the orientation of the magnetic field only. The only exceptions were the Zeeman effect observations, which are possible in some molecular clouds, and the combination of Pulsar rotation measure and dispersion measure. In general we must invoke the argument of equipartition to determine the magnetic field strength.

The energy spectrum of relativistic electrons is;

N(E) dE = N0 E-nu dE .

For equipartition of energy between magnetic field and relativistic electrons we have:

B2 / B pi = k integE2E1 E N(E) dE ,

where E1 and E2 are the lower and upper limits of the energy spectrum (and correspond to the cutoff frequencies nu1 and nu2). The factor k is the ratio of the total energy of cosmic rays to the electron energy. The field strength B (in Gauss) is:

B = 2.3(k A e)2/7

(e.g. see Moffat, 1973). In the above equation e is the volume emissivity (in erg sec-1 cm-3), A is given by;

A = C (a + 1) / (a + 1/2) (V2a+1/2 - V1a+1/2) / (V2a+1 - V1a+1/2)

with C = 1.057 × 1012 cgs units, a = (nu-1) / 2 is the spectral index. The emissivity e is also given by:

e = 4 pi / l integV1V2 Inu dv

where Inu is the intensity and l the length (cm) of the source. The parameters k and nu1(Hz) are taken often as 100 and 107 respectively (e.g. Sofue et al., 1986).

Although the fundamental question of the applicability of equipartition is often subject of heated discussions the concept as such has stood many attacks. It is a way an 'economical' concept, where the energy between two reservoirs is minimized.

6. THE INTERPRETATION OF MAGNETISM IN GALAXIES

Two general alternative models for the origin of magnetic fields in galaxies have been proposed;- the primodial model where the fields came through the compression of a relict field or the dynamo scenario where the field is generated through the amplification of a seed field in a galactic rotation. The primodial field model was developed in some detail by Piddington, (1964, 1978, 1981). This seemed at first feasible when the primodial intergalactic field was put at 10-8 Gauss or more. A compression by a factor of 100 would bring the fields into the observed range of a few µG. However as a result of more recent observations values for the magnetic field were estimated to be 5 < Bt < 50 µG. Also more recent estimates of the intergalactic magnetic field suggest that the upper limits are 10-9 - 10-10 G. Also it was pointed out by Parker (1979) that in presence of turbulence the primodial field would be dissipated in 107 years. Clearly these two arguments do not allow sufficient room for the primodial field hypothesis.

All the recent theoretical investigations have been directed towards the interpretation of the magnetic fields in galaxies in the context of the turbulent hydromagnetic dynamo theory. Originally the explanation of the magnetism of the Earth, the Sun and Planets determined the development of the dynamo theory. (e.g. Parker, 1955, 1971, 1979; Steenbeck et al., 1966; Krause and Rädler 1980). The application of the dynamo theory to galaxies was investigated by Parker (1971) and Vainshtein and Ruzmaikin (1971). This idea was reinvestigated in some detail in view of the new observational data by Ruzmaikin and Shukurov (1981). The difficulty at first was that the solution of the dynamo equation was for the basic mode only. Since the observations showed magnetic fields with a spiral-like structure this dynamo interpretation was obviously inapplicable. In addition investigations of the Faraday rotation in M51 by Tosa and Fujimoto (1978) suggested that the field was 'bisymmetric', [BSS], i.e. with the field orientation going along a spiral arm into the nucleus and coming out of the nucleus with unchanged field direction. This is in contrast to the axisymmetric [ASS] configuration, where the field lines point in or out of the nucleus.

The basic dynamo equation is given by (e.g. Krause and Rädler, 1980):

dB / dt = v × (u × B) + k v2 B + v × (aB)

with

v.B = 0

the first term of the dynamo equation describes the large-scale velocity field (usually given by u = Omega × r), the second term gives the mean helicity of the turbulence and the third one the turbulent magnetic diffusity.

Parker (1971) has suggested a concept of the 'aw-dynamo', where a mean toroidal magnetic field is generated by the non-uniform (differential) rotation w from an original poloidal magnetic field. The poloidal field is regenerated from the toroidal field by the effects of cyclonic convection (the a-effect). Parker described the dynamo in the 'slab' geometry, i.e. a thin layer of infinite extended electrically conducting gas in cyclonic turbulent motion subject to a large shear.

A spherical dynamo without differential rotation, (which is particularly applicable to the Earth and the Planets), has been investigated by Krause and Steenbeck (1967). This dynamo with constant a leads to an 'a2-dynamo'. A detailed study of the stability of a2 dynamos was given by Krause and Meinel (1988).

In fact solutions of the dynamo equation in other geometries are few. An exception, which may be applicable to galaxies, is the solution of the oblate spheroid by Stix (1975). More recently a partial solution for a slender torus was given by Grosser (1988) which may apply to the situation in the nucleus of a galaxy.

Since the observations of magnetic fields in galaxies suggest a dominance of the BSS field structure numerous theoretical papers were published to explain this observational fact. Also the problem of the fields above the plane of the disc (in the halo) were investigated. The solution of the dynamo equation for many modes (Ruzmainin et al., 1985; Baryshnikova et al., 1987; Krasheninnikova et al., 1989) showed that the co-existence of the BSS and ASS modes was possible in the context of the dynamo theory. A special investigation of the dynamo solution leading to the BSS case was given by Sawa and Fujimoto (1986) and Fujimoto and Sawa (1987). The extension to three dimensions was discussed by Sawa and Fujimoto (1987). Further attempts to model three dimensional situations are given by Strachenko and Shukurov (1989). The question of the growth rates of different modes and the stability of the nonlinear dynamo was treated by Brandenburg et al. (1989).

In spite of the great activity in the understanding of the dynamo many questions are open. There is still some lingering hope that compression of the primodial field could be used to explain some of the observed phenomena. The role of reconnections, a perennial discussion point, is still unclear. The applicability of equipartition, so often used to explain observational results, is still not universally accepted. The role of the local magnetic fields (stellar fields, pulsars, supernovae, bi-polar sources, molecular clouds, etc.) in relation to the global magnetic fields is also unclear. The reason for the dominance of the BSS field structure in some galaxies has not been as yet explained. The interplay of theory and observations is doing a lot of good in advancing our understanding but; 'all is not well in the house of magnetic fields'.

7. THE SEED FIELD

Both the primodial field concept and the galactic dynamo theory require some magnetic field to start with. The dynamo has the advantage that it can amplify the seed magnetic field by a factor of 103 or more. In the non-linear dynamo the amplification factor could be even greater. With the accepted values of intergalactic magnetic field of ~ 10-10 Gauss (Ruzmaikin and Sokoloff, 1977) we may have to look for other sources of seed fields for amplification by a dynamo process.

One of the most important processes for the creation of a minute magnetic field is the 'Biermann battery' (Biermann, 1950). When applied to a galaxy the concept requires small turbulent cells which through charge separation would give small currents and hence magnetic fields. The concept of transferring this scenario to galactic scales failed (e.g. Hoyle, 1958) since enormous electromotive force would be required. One way out, which was studied by Hoyle and Ireland (1961), was to postulate helical magnetic fields.

A recent development in this area comes from the observations of CO rings and of poloidal magnetic fields in many mildly active galaxies. CO rings have been seen in the inner parts of M82 (Lo et al., 1987; Nakai et al., 1987; Loiseau et al., 1990), NGC1097 (Gerin et al., 1988), NGC4945, NGC1808, NGC 1068, etc. Also in these galaxies strong evidence for poloidal magnetic fields (Z-fields) was found either by optical studies or in radio polarization. This scenario was studied by Lesch et al. (1989). By applying the battery effect to give charge separation in the inner CO ring a small seed field can be created. This in turn can be amplified by compression and turbulent stretching. Possibly the poloidal field in the nucleus of a galaxy can in turn be amplified to give the observed azimuthal fields in the spiral arms.

8. THE 'FUTURE' OF MAGNETIC FIELDS

It seems that each decade in astrophysics had its fashion subject. Magnetic fields were 'in' in the 1950's. Then came the gravity fashion with the successes of the density wave theory, mergers etc. The 1970's were the years of the interstellar medium with the monumental discoveries of molecules, studies of UV absorption lines, the use of the IRAS satellite data etc. Now in the 1980's it seems we are finding it to be necessary to combine the results on all the various fashions in the hope of understanding the universe. The first IAU symposium on Galactic and Intergalactic Magnetic Fields was held in Heidelberg in June 1989. A simple conclusion can be given after this symposium. We have many astounding pieces of information about the magnetic fields in the Earth, the Sun, the Planets, our Galaxy, and external galaxies. We even know that there is a field in the clusters of galaxies. We have detailed theories that can explain a host of details of various astronomical objects. However we still have a long way to go before we have an overall understanding of the role of magnetic fields in astrophysics.

REFERENCES

BOOKS

  1. Parker E. N. Cosmical Magnetic Fields 1979, Claredon Press, Oxford.
  2. Krause F. and Rädler K. H. Mean Field Magnetohydrodynamics and Dynamo Theory 1980, Pergamon Press.
  3. Beck R. and Gräve R. Interstellar Magnetic Fields 1987, Springer-Verlag.
  4. Zeldovich Ya. Ruzmaikin A. A. and Sokoloff D. D. Magnetic Fields in Astrophysics 1987, Gordon & Breach.
  5. Asseo E. and Gresillon D. Magnetic Fields and Extragalactic Objects 1987, Cargese Workshop, Edition de Physique.
  6. Ruzmaikin A. A. Shukurov A. M. and Sokoloff D. D. Magnetic Fields in Galaxies 1988, Kluwer Academic Publishers.
  7. Beck R. Kronberg P. P. and Wielebinski R. Galactic and Intergalactic Magnetic Fields, Proceedings I.A.U. Symposium No.140, Kluwer Academic Publishers, (in press).

REVIEW ARTICLES

  1. Gardner F. F. and Whiteoak J. B. 1966, Ann. Rev. Astron. Astrophys., 4, 245.
  2. Heiles C. 1976, Ann. Rev. Astron. Astrophys., 14, 1.
  3. Verschuur G. L. 1979, Fund. Cosmic Phys., 5, 113.
  4. Blandford R. D., 1983, Astron. J., 88, 245.
  5. Sofue Y., Fujimoto M. and Wielebinski R. 1986, Ann. Rev. Astron. Astrophys., 24, 459.
  6. Beck R. 1986, IEEE Trans. Plasma Science, PS-14, 740.
  7. Asseo E. and Sol H. 1987, Physics Reports, 148, 309.
  8. Heiles C. 1987, in Interstellar Processes eds. D. J. Hollenbach and H. A. Thronson Jr., p. 171, D. Reidel Publ. Comp.
  9. Zweibel E. G. 1987, in Interstellar Processes eds. D. J. Hollenbach and H. A. Thronson Jr., p. 195, D. Reidel Publ. Comp.
  10. Ruzmaikin A. A., Sokoloff D. D. and Shukurov A. M. 1988, Nature, 336, 341.

GENERAL REFERENCES

  1. van Albada G. D. 1978, Ph.D. Thesis, Leiden University.
  2. Allen R. J., Baldwin J. E., Sancisi R. 1978, Astron. Astrophys., 62, 397.
  3. Appenzeller I. 1967, Publ. Astron. Soc. Pacific, 79, 600.
  4. Bajaja E., Dettmar R. -J., Hummel E., Wielebinski R. 1988, Astron. Astrophys., 202, 35.
  5. Baryshnikova Y., Ruzmaikin A. A., Sokoloff D. D., Shukurov A. 1987, Astron. Astrophys., 177, 27.
  6. Beck R. 1982, Astron. Astrophys., 106, 121.
  7. Beck R., Berkhuijsen E. M., Wielebinski R. 1978, Astron. Astrophys., 68, L27.
  8. Beck R., Berkhuijsen E. M., Wielebinski R. 1980, Nature, 283, 272.
  9. Beck R., Klein U., Wielebinski R. 1987, Astron. Astrophys., 186, 95.
  10. Beck R., Loiseau N., Hummel E., Berkhuijsen E. M., Gräve R., Wielebinski R. 1989, Astron. Astrophys., 222, 58.
  11. Behr A. 1959, Veröff. U. Sternw. Göttingen, No.126.
  12. Berkhuijsen E. M., Brouw W. N., 1963, Bull. Astron. Inst. Netherland, 17, 185.
  13. Biermann L. 1950, Z.Naturf., 5a, 65.
  14. Bingham R. G., McMullan D., Pallister W. S., White C., Axon D. J., Scarrott S. M. 1976, Nature, 259, 463.
  15. Brandenburg A., Krause F., Meinel R., Moss D., Tuominen I. 1989, Astron. Astrophys. 213, 411.
  16. Buczilowski U., Beck R. 1987, Astron. Astrophys. Suppl., 68, 171.
  17. Crutcher R. M., Kazes H., Troland T. H. 1987, Astron. Astrophys., 181, 119.
  18. Davis L., Greenstein J. L. 1951, Astrophys. J., 114, 206.
  19. Ekers R., Sancisi R. 1977, Astron. Astrophys., 54, 973.
  20. Ellis R. S., Axon D. J. 1978, Astrophys. Space Sc., 54, 425.
  21. Elvius A. 1978, Astron. Astrophys., 65, 233.
  22. Elvius A., Hall J. S. 1965, Astron. J., 70, 138.
  23. Fermi E. 1949, Phys. Rev., 171, 1169.
  24. Fiebig D., Güsten R. 1989, Astron. Astrophys., 214, 333.
  25. Fujimoto M., Sawa T. 1987, Publ. Astron. Soc. Japan, 39, 375.
  26. Gerin M., Nakai N., Combes F. 1988, Astron. Astrophys., 203, 44.
  27. Ginzburg V. L., Syrovatskij S. I. 1969, Ann. Rev. Astron. Astrophys., 7, 375.
  28. Gräve R., Klein U., Wielebinski R. 1990, Astron. Astrophys., 238, 39.
  29. Grosser H. 1988, Astron. Astrophys., 199, 235.
  30. Hall J. S. 1949, Science, 109, 166.
  31. Harnett J. I., Beck R., Buczilowski U. 1989a, Astron. Astrophys., 208, 32.
  32. Harnett J. I., Haynes R. F., Klein U., Wielebinski R. 1989b, Astron. Astrophys., 216, 39.
  33. Harnett J. I., Haynes R. F., Wielebinski R., Klein U. 1990, Proc. Astron. Soc. Australia, 8, 257.
  34. Haynes R. F., Klein U., Wielebinski R., Murray J. D. 1986, Astron. Astrophys., 159, 22.
  35. Haynes R. F. et al., 1990, Proc IAU Symp. No. 140, p. 205.
  36. Hildebrand R. H. 1988, Astro. Lett., 26, 263.
  37. Hiltner W. A. 1949, Ap. J., 109, 471.
  38. Hiltner W. A. 1958, Astrophys. J., 128, 9.
  39. Horellou C., Beck R., Klein U., Krause M. 1990, Proc. IAU Symp. No. 140, p. 211.
  40. Hoyle F. 1958, in La Structure et l'Evolution d'Univers, XI Solvey Conference, p. 53.
  41. Hoyle F., Ireland J. G. 1961, Mon. Not. Roy. Astr. Soc., 122, 35.
  42. Hummel E., Dettmar R. -J., Wielebinski R. 1986, Astron. Astrophys., 166, 97.
  43. Hummel E., Lesch H., Wielebinski R., Schlickeiser R. 1988, Astron. Astrophys., 197, L29.
  44. Hummel E., Krause M., Lesch H. 1989, Astron. Astrophys., 211, 266.
  45. Junkes N., Fürst E., Reich W. 1987, Astron. Astrophys. Suppl., 69, 451.
  46. Klein U., Beck R., Buczilowski U., Wielebinski R. 1982, Astron. Astrophys., 108, 176.
  47. Klein U., Urbanik M., Beck R., Wielebinski R. 1983, Astron. Astrophys., 127, 177.
  48. Klein U., Wielebinski R., Beck R. 1984, Astron. Astrophys., 133, 19.
  49. Klein U., Wielebinski R., Morsi H. W. 1988, Astron. Astrophys., 190, 41.
  50. Klein U., Wielebinski R., Haynes R. F., Malin D. F. 1989, Astron. Astrophys., 211, 280.
  51. Krasheninnikova Y., Ruzmaikin A. A., Sokoloff D. D., Shukurov A. 1989, Astron. Astrophys., 213, 19.
  52. Krause F., Steenbeck M. 1967, Z.Naturf., 22a, 671.
  53. Krause F., Meinel R. 1988, Geophys. Astrophys. Fluid Dyn., 43, 95.
  54. Krause M., Hummel E., Beck R. 1989b, Astron. Astrophys., 217, 4.
  55. Krause M., Beck R., Hummel E. 1989a, Astron. Astrophys., 217, 17.
  56. Kronberg P. P., Biermann P., Schwab F. R. 1985, Astrophys. J., 291, 693.
  57. van der Kruit P. C., Oort J. H., Mathewson D. S. 1972, Astron. Astrophys., 21, 169.
  58. Lesch H., Crusius A., Schlickeiser R., Wielebinski R. 1989, Astron. Astrophys., 217, 99.
  59. Lo K. Y., Cheung K. M., Masson C. R., Phillips T. G., Scott S. L., Woody D. P. 1987, Astrophys. J., 312, 574.
  60. Loiseau N., Klein U., Greybe A., Wielebinski R., Haynes R. F. 1987, Astron. Astrophys., 178, 62.
  61. Loiseau N., Nakai N., Sofue Y., Wielebinski R., Reuter H. -P., Klein U. 1990, Astron. Astrophys., 228, 331.
  62. Lyne A., Smith Graham F. 1989, Mon. Not. Roy. Astr. Soc., 237, 533.
  63. MacLeod J. M., Vallee J. P., Broten N. W. 1988, Astron. Astrophys Suppl., 74, 63.
  64. Martin P. G., Shawl S. J. 1982, Astrophys. J., 253, 86.
  65. Mathewson D. S., Milne D. K. 1965, Austr. J. Phys., 18, 635.
  66. Mathewson D. S., Ford V. L. 1970, Astron. J., 75, 778.
  67. Mathewson D. S., Ford V. L. 1970, Mem. Roy. Astr. Soc., 74, 139.
  68. Mathewson D. S., van der Kruit P. C., Brouw W. N. 1972, Astron. Astrophys., 17, 468.
  69. Matsumuna M., Seki M. 1989, Astron. Astrophys., 209, 8.
  70. Mayer C. H., McCullough T. P., Sloanaker R. M. 1957, Astrophys. J., 126, 468.
  71. Meyer 1920, Lick Obs. Bull., 10, 68.
  72. Moffat A. T. 1973, in Galaxies and the Universe, eds. Sandage et al., 9, Chapter 7, Chicago Uni. Press.
  73. Nakai N., Hayashi M., Handa T., Sofue Y., Hasagawa T. 1987, Publ. Astron. Soc. Japan, 39, 685.
  74. Neininger N. 1989, Dipl. Thesis, Bonn University.
  75. Öhman Y. 1942, Stockholm Obs. Bull., 10, 68.
  76. Parker E. N. 1955, Astrophys. J., 122, 293.
  77. Parker E. N. 1971, Astrophys. J., 163, 255.
  78. Piddington J. H. 1964, Mon. Not. Roy. Astr. Soc., 128, 345.
  79. Piddington J. H. 1978, Astrophys. Space Sci, 59, 237.
  80. Piddington J. H. 1981, Astrophys. Space Sci, 80, 457.
  81. Purcell E. M. 1979, Astrophys. J., 231, 404.
  82. Reich W. 1989, Proc IAU Symp. No. 136, p. 265.
  83. Reich W., Sofue Y., Wielebinski R., Seiradakis J. H. 1988, Astron. Astrophys., 191, 303.
  84. Ruzmaikin A. A., Sokoloff D. D. 1977, Astron. Astrophys., 58, 247.
  85. Ruzmaikin A. A., Shukurov A. M. 1981, Sov. Astron., 25, 553.
  86. Ruzmaikin A. A., Sokoloff D. D., Shukukov A. M. 1985, Astron. Astrophys., 148, 335.
  87. Sawa T., Fujimoto M. 1986, Publ. Astron. Soc. Japan, 38, 132.
  88. Sawa T., Fujimoto M. 1988, in Proc. International Workshop, Cargese, eds. E. Asseo and H. Sol.
  89. Scarrott S. M., White C., Pallister W. S., Solinger A. B. 1977, Nature, 265, 32.
  90. Scarrott S. M., Ward-Thompson D., Warren-Smith R. F. 1987, Mon. Not. Roy. Astron. Soc., 224, 299.
  91. Schmidt Th. 1970, Astron. Astrophys., 6, 294.
  92. Schmidt Th. 1976, Astron. Astrophys. Suppl., 24, 357.
  93. Segalovitz A., Shane W. W., de Bruyn A. 1976, Nature, 264, 222.
  94. Simard-Normandin M., Kronberg P. P., Button S. 1981, Astrophys. J. Suppl., 45, 97.
  95. Sofue Y., Fujimoto M. 1983, Astrophys. J., 265, 722.
  96. Sofue Y., Klein U., Beck R., Wielebinski R. 1985, Astron. Astrophys., 144, 257.
  97. Spoelstra T. A. -Th. 1984, Astron. Astrophys., 135, 238.
  98. Steenbeck M., Krause F., Rädler K. H. 1966, Z.Naturf., 21a, 369.
  99. Stix M. 1975, Astron. Astrophys., 42, 85.
  100. Strachenko S. V., Shukurov A. M. 1989, Astron. Astrophys., 214, 47.
  101. Sukumar S., Klein U., Gräve R. 1987, Astron. Astrophys., 184, 71.
  102. Sukumar S., Allen R. J. 1990, Proc. IAU Symp. No. 140, p. 215.
  103. Tosa M., Fujimoto M. 1978, Publ. Astron. Soc. Japan, 30, 315.
  104. Vainstein S. I., Ruzmaikin A. A. 1971, Astron. J. (UdSSR), 48, 902.
  105. Vallee J. P. 1988, Astron. J., 95, 750.
  106. Wagner S. J., Dettmar R. -J., Bender R. 1989, Astron. Astrophys., 215, 243.
  107. Westerhout G., Seeger Ch. L., Brouw W. N., Tinbergen J. 1962, Bull. Astron. Inst. Neth., 16, 187.
  108. Wielebinski R., Shakeshaft J. S., Pauliny-Toth I. I. K. 1962, Observatory, 82, 158.
  109. Wielebinski R., Shakeshaft J. S. 1964, Mon. Not. Roy. Astron. Soc., 128, 19.
  110. Wielebinski R., von Kap-herr A. 1977, Astron. Astrophys., 59, L17.