2.2. Connection with thermal instability

There is an intimate connection between the existence of thermal phases and the thermal stability of a system: any system exhibiting multiphase equilibria must be thermally unstable over a range of thermodynamic parameters. The thermal stability of astrophysical gases was first studied systematically by Field (1965). His instability criterion was generalized to non-equilibrium systems by Balbus (1986a), who found the following condition for instability:

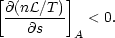
(2)

Here s is the entropy per hydrogen nucleus and A is some thermodynamic variable which is held constant during the perturbation. In equilibrium, = 0 and this reduces to Field's instability criterion

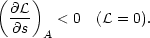
(3)

In general, s is a complicated function of n, T, and the state of ionization of the gas. However, in many applications the gas is almost completely ionized and the entropy function may be approximated by the expression for an ideal gas, s ~ lnpV^5/3 + const. If A is some power law combination of p and V, then T(s / T)_A is a constant specific heat which is positive for cases of interest. The instability criterion then becomes

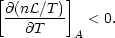
(4)

Since the cooling time is proportional to T / n, this criterion can be rephrased as stating that instability occurs if the cooling time increases with temperature (Balbus 1986a).

If the gas is in equilibrium ( = 0), the instability criterion (4) reduces to

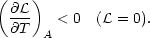
(5)

Field (1965) showed that for the equilibrium case the isobaric criterion ( / T)_p < 0 is usually the correct one to apply. However, if the system is large enough that the sound crossing time is long compared to the heating or cooling times, then for long wavelengths the isochoric criterion ( / T)_V < 0 is applicable.

The stability criterion (5) may be interpreted geometrically in terms of the equilibrium curve (Figure 1). Typically the cooling region (n > ) lies above the heating region because the cooling rate usually increases faster with n and T than does the heating rate. If, on the other hand, the heating region lay above the cooling region, then over much of the curve (wherever p(V) is single-valued) one would have ( / T)_V < 0 and the equilibrium would be isochorically unstable. In this case systems large enough that the sound crossing time is much greater than the heating and cooling times could be unstable even where smaller systems are isobarically stable. This situation does not arise in practice and we therefore assume that the cooling region lies above the heating region in the p - V plane, as shown in Figure 1.

The slope of the equilibrium curve in the p - V plane is directly related to the stability of the system since

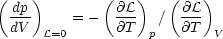
(6)

(Field 1965). For cases in which p(V) is single valued (as in Fig. 1 a-c), the condition that the cooling region lie above the heating region implies that the system is isochorically stable, so that the denominator in equation (6) is positive; hence, in this case isobarically stable regions have a negative slope in the p - V plane, whereas unstable regions have a positive slope. The condition for a multiphase equilibrium is that V(p) be a multivalued function, which is equivalent to having d lnp / d ln V change sign. Thus, a necessary and sufficient condition for the existence of a multiphase equilibrium is that the system be thermally unstable over a finite range of V. This proves the assertion at the beginning of this section. Fig. 1 d illustrates a case in which p(V) is multivalued over a range in V. Such a system can exhibit both isochoric and isobaric instability, where the equilibrium curve has a negative slope in the p - V plane.

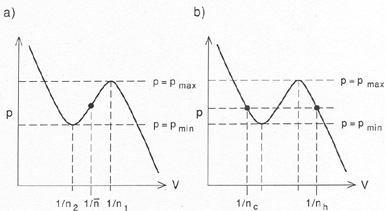
A system with two stable phases (e.g., Fig. 1b) may be used to illustrate the inevitability of multiple phases under certain circumstances. A characteristic feature of two-phase systems is that the cold phase cannot exist below some minimum pressure p_min, while the hot phase cannot exist above some maximum pressure p_max. The condition that there be two stable phases implies that p_max > p_min. Now consider a homogeneous system with a density n₁ < < n₂, as shown in Fig. 2a. Such a system is clearly unstable in its homogeneous state. However, it is always possible to stabilize the system by making it inhomogeneous, while keeping the mean density constant (Fig. 2b). The trick is to put most of the mass in the cold phase, with density n_c > n₂, while a small fraction of the matter forms a hot intercloud medium, with density n_h < n₁ and temperature T_h. Pressure balance requires n_c / n_h = T_h / T_cl. If f is the filling factor in cold gas, then the mean density constraint is = (1 - f)n_h + fn_c, and f satisfies T_cl / T_h << f << 1 if n₁ << << n₂.

Figure 2. Inevitability of thermal instability in a system with a fixed mean density and variable pressure p. Equilibrium curve is identical to that in Fig. 1b. a) Homogeneous state is thermally unstable. b) In the stable two-phase state, most of the mass is in the cold phase with nc > n2 and a small filling factor.