


1.3. Conservation of momentum and energy?
Are total momentum and energy conserved in cosmology? This is a nontrivial question because the canonical momentum and Hamiltonian differ from the proper momentum and energy.
Consider first the momentum of a particle in an unperturbed Robertson-Walker
universe. With no perturbations,
 = 0 so that
Hamilton's equation for p becomes dp /
d
= 0 so that
Hamilton's equation for p becomes dp /
d =
-am
=
-am
 = 0, implying that
the canonical momentum p is conserved. But, the
proper momentum
mv = a-1p measured
by a comoving observer decreases as a
increases. What happened to momentum conservation?
= 0, implying that
the canonical momentum p is conserved. But, the
proper momentum
mv = a-1p measured
by a comoving observer decreases as a
increases. What happened to momentum conservation?
The key point is that v = dx /
d is measured using a
non-inertial
(expanding) coordinate system. Suppose, instead, that we choose
v
to be a proper velocity measured relative to some fixed origin. Momentum
conservation then implies v = constant (if
is measured using a
non-inertial
(expanding) coordinate system. Suppose, instead, that we choose
v
to be a proper velocity measured relative to some fixed origin. Momentum
conservation then implies v = constant (if

 = 0, as
we assumed above). At
= 0, as
we assumed above). At  =
=
 1 and
1 and
 2, the particle is at
x1 and x2,
respectively. Because dx /
d
2, the particle is at
x1 and x2,
respectively. Because dx /
d gives
the proper velocity relative to a comoving observer at the
particle's position, at
gives
the proper velocity relative to a comoving observer at the
particle's position, at
 1 we have
dx /
d
1 we have
dx /
d = v -
(
= v -
( /a)1
x1, while at
/a)1
x1, while at
 2,
dx /
d
2,
dx /
d = v -
(
= v -
( / a)2
x2. (The proper velocity relative to the fixed
origin is v in both cases, but the Hubble velocity at the
particle's position
- the velocity of a comoving observer - changes because the
particle's position has changed.) Combining these, we find
[
/ a)2
x2. (The proper velocity relative to the fixed
origin is v in both cases, but the Hubble velocity at the
particle's position
- the velocity of a comoving observer - changes because the
particle's position has changed.) Combining these, we find
[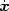 (
( 2) -
2) -
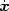 (
( 1)] /
(
1)] /
( 2 -
2 -
 1)
1)
 -
(
-
( /
a)[x(
/
a)[x( 2) -
x(
2) -
x( 1)]
/ (
1)]
/ ( 2 -
2 -
 1) +
O(
1) +
O( 2 -
2 -
 1) or, in the
limit
1) or, in the
limit  2 -
2 -
 1
1
 0,
d2x /
d
0,
d2x /
d 2 =
- (
2 =
- ( /a)
dx /
d
/a)
dx /
d .
This is precisely our comoving equation of motion in the case
.
This is precisely our comoving equation of motion in the case

 = 0.
Thus, the "Hubble drag" term
(
= 0.
Thus, the "Hubble drag" term
( /
a)dx /
d
/
a)dx /
d is merely a "fictitious force" arising from the use of non-inertial
coordinates. Stated more physically, the particle appears to slow down
because it is continually overtaking faster moving observers.
is merely a "fictitious force" arising from the use of non-inertial
coordinates. Stated more physically, the particle appears to slow down
because it is continually overtaking faster moving observers.
Energy conservation is more interesting. Let us check whether the
Hamiltonian H(x, p,
 ) is conserved. Using Hamilton's
equations for a single particle, we get
) is conserved. Using Hamilton's
equations for a single particle, we get
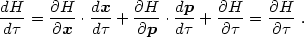 |
(1.17) |
Using H = p2 / (2am) +
am , we
obtain
dH / d
, we
obtain
dH / d =
- (
=
- ( /
a)(p2 / 2am) + md
(a
/
a)(p2 / 2am) + md
(a ) /
d
) /
d which is nonzero
even if
d
which is nonzero
even if
d /
d
/
d = 0. Is this lack
of energy conservation due to the use of non-inertial coordinates? While
the appearance of a Hubble-drag term may suggest this is the case, if we
wish to obtain the total Hamiltonian (or energy) for a system of particles
filling all of space, we have no choice but to use comoving coordinates.
= 0. Is this lack
of energy conservation due to the use of non-inertial coordinates? While
the appearance of a Hubble-drag term may suggest this is the case, if we
wish to obtain the total Hamiltonian (or energy) for a system of particles
filling all of space, we have no choice but to use comoving coordinates.
Perhaps the Hamiltonian is not conserved because it is not the proper energy. To examine this possibility, we use the Hamiltonian for a system of particles in comoving coordinates, with H = a(T + W). The proper kinetic energy (with momenta measured relative to comoving observers) is
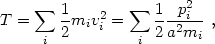 |
(1.18) |
while the gravitational energy W is given in eq. (1.11).
Holding fixed the momenta, we see that a2T is a
constant, implying
 (aT) /
(aT) /

 =
-
=
-  T. Similarly,
holding fixed the particle positions, we find that
a
T. Similarly,
holding fixed the particle positions, we find that
a is a
constant, implying
is a
constant, implying
 (aW) /
(aW) /

 = 0. We thus obtain the
Layzer-Irvine equation
(Layzer 1963,
Irvine 1965)
= 0. We thus obtain the
Layzer-Irvine equation
(Layzer 1963,
Irvine 1965)
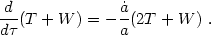 |
(1.19) |
Total energy (expressed in comoving coordinates) is not conserved in
Newtonian cosmology. (This is also the case in GR - indeed, there is
generally no unique scalar for the total energy in GR.) However, if
almost all of the mass is in virialized systems obeying the classical
virial theorem
2T + W  0, we recover approximate total energy conservation.
0, we recover approximate total energy conservation.