2.3. Linear instability 2: entropy fluctuations and isocurvature mode

Entropy gradients act as a source term for density perturbation growth. Using eq. (2.10) and repeating the derivation of the linear acoustic equation, we obtain (for c_s² << c²)

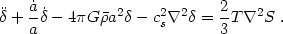(2.20)

For adiabatic evolution, 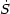= 0, so what counts is the initial entropy gradient. Entropy gradients may be produced in the early universe by first-order phase transitions resulting in spatial variations in the photon/baryon ratio or other abundance ratios. If there were no entropy gradients present before such a phase transition, then the entropy variations can only have been produced by nonadiabatic processes. (This may explain the "adiabatic vs. isocurvature" nomenclature used by some cosmologists.) In practice, these entropy fluctuations are taken as initial conditions for subsequent adiabatic evolution.

Equation (2.20) is not applicable to the early universe because it assumes the matter is a one-component nonrelativistic gas. However, the behavior of its solutions are qualitatively similar to those for a relativistic multi-component gas and so its analysis is instructive.

The isocurvature mode is given by the particular solution of density perturbation growth having = = 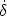0 but ²S 0 at some early initial time _i. The initial conditions may be regarded as a perturbation in the equation of state in an otherwise unperturbed Robertson-Walker (constant spatial curvature) spacetime, accounting for the name "isocurvature." Variations in entropy at constant density correspond to variations in pressure, which lead through adiabatic expansion to changes in the density. Therefore, initial entropy fluctuations seed density fluctuations.

The solution to eq. (2.20) is obtained easily in Fourier space using the source-free (isentropic) solutions _±(k, ):

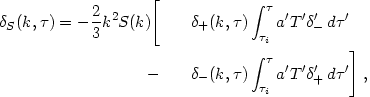(2.21)

where primes are used to indicate that the variables are evaluated at = '. We see that both growing and decaying density perturbations are induced. After the source (aT_) becomes small, the density fluctuations evolve the same way as isentropic fluctuations - e.g., they oscillate as acoustic waves if kc_s >> 1. 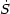To reinforce the point about nomenclature made earlier, I note that in our approximation, both isocurvature and "adiabatic" (i.e., isentropic) modes are adiabatic in the sense of thermodynamics: = 0 after the initial moment. For a realistic multi-component gas the evolution is not truly adiabatic, but that is a complication we shall not consider further. In the literature, modes are described as being adiabatic or isocurvature depending only on whether the initial density is perturbed with negligible initial entropy perturbation, or vice versa.