2.2. Outline of the "beam "model

Continuous supply of energy into radio components was first invesigated by Rees [1] who proposed that a galactic nucleus contained a source of low frequency ( 1 kHZ) electromagnetic waves (e.g., a cluster of 10⁶ pulsars radiating magnetic dipole radiation at their rotation frequency). The radiation would escape most easily from the nuclear region along the rotation axis (cf. [2] and [3]) and a channel would steadily be evacuated along which the low frequency waves could travel. This cavity would probably not contain much plasma, and those particles that were present would become relativistic. The plasma frequency would then be much lower than that associated with the surrounding medium and the waves would be naturally self-focussed; giving, at least qualitatively, the observed collimation.

Low frequency waves could fulfill a dual function at the hot spots, being both capable of accelerating GeV electrons and providing an electromagnetic field for them to radiate in. However, a similar model [4] was unable to account for the observations of the Crab Nebula and it was discovered that these waves would almost certainly be at the mercy of a variety of rapid parametric instabilities and resonant absorption processes. Subsequently, a more general viewpoint was taken [5 - 7] and it was suggested that the working substance behaved approximately as a "light" fluid. That is to say, the beams consist of fast moving hot plasma, probably permeated by static magnetic fields and electromagnetic wave modes. (In fact, as emphasised by Scheuer [6], the results are qualitatively unchanged if the beam consists of particles that undergo reflections at the channel walls, or relativistic particles streaming along a diverging magnetic field and conserving their adiabatic invariants.)

Although the collision mean free paths of relativistic particles in radio sources are very long, a fluid treatment can be justified because we know magnetic fields are present. The gyroradius of a relativistic particle of energy moving in a magnetic field B (Gauss) is ~ 10^-12( / m_p c²)B^-1 pc. This is typically very small, compared to all relevant scales, for B 10^-6 G. Collective plasma effects also may reduce the effective mean free path (cf. the solar wind, which can in many contexts be regarded as a fluid, even though collisional lengths are very large).

If all the particles in the beam are ultrarelativistic, then p = 1/3 c² and the sound speed is c_s (c / 3). Bernoulli's equation is then simply _bulk = (1 - v² / c²)^-1/2 = (P / p₀)^-1/4; and the mean random energy per relativistic particle, measured in the moving frame, varies as _bulk^-1. If the magnetic field contributes significantly to the total energy density and has a preferred orientation, then the pressure and magnetosonic velocities are of course anisotropic. The Debye length is also very small compared with the scale of the flow. This means that the relativistic plasma must be essentially neutral (in contrast to laboratory-scale electron beams) and the relativistic generalisation of ordinary MHD is applicable. There will be no electric field in a frame sharing the means plasma velocity ; but in a non-moving frame, of course, the electric and magnetic field energies would be comparable if c. In fact, it is not necessary for the model that the sound speed c_s in the beam actually be relativistic: the only requirement is that c_s be larger than the gravitational escape velocity, so that the direct effects of gravity on the beam material are negligible.

Suppose that a collimated beam has been established (by processes which we consider later). At a given time, the beam will have evacuated a tube or channel out to some location where it impinges on the external medium at a "working surface" which itself advances out at speed V. If the power flowing in the beam, L, is approximately conserved and stationary, then approximating the channel as a cylinder of radius r, we balance momentum fluxes at the "working surface" to obtain

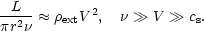
(1)

where is the speed of the beam, _ext, the external density, and c_s the internal sound speed. If the beam consists of relativistic plasma then c and relativistic fluid mechanics must be used. The pressure, p on the walls of the channel is given by

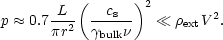
(2)

This must be approximately balanced by a static external pressure if the walls are not to expand, any difference in pressure p leading to a transverse expansion speed (p / _ext)^1/2. However the ratio of the energy to the momentum supplied by the beam over the lifetime of the source is ~ V which exceeds the energy/momentum ratio required to sweep away the external medium by ~ / V >> 1. The surplus (or waste) energy must then not accumulate near the "working surface" but be deposited within a "cocoon" surrounding the beam, which it is natural to identify with the low-surface-brightness tails.

The beam velocity is generally assumed to be supersonic and one possible way of maintaining this beam in a quasi-stationary state, and creating a high Mach number flow, is by means of a de Laval nozzle [7]. Suppose that there exists some continuous source of hot fluid in the nucleus, surrounded by a denser material trapped by the gravitational potential well. At first an almost spherical bubble will be inflated which can expand most rapidly along the rotation axis and eventually will be able to escape from the nuclear region. If the source is sufficiently powerful, two anti-parallel channels of hot fluid will be set up which can eventually provide the continuous energy supply for the radio components. If the flow is assumed to be stationary and isentropic then the fluid velocity will increase as the pressure decreases. When the pressure has halved the flow becomes transonic and the cross-sectional area is minimised. In this way a directed nozzle can be established. The radius of the channel at the nozzle is related to the total energy discharge, L, stagnation pressure, p₀, and sound speed, c_s by:

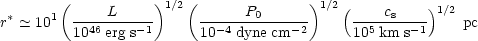
(3)

We return later to discuss further the collimation mechanism (the "nozzle" is only one of several possibilities) and the scale on which it is established. As far as the extended components are concerned, however, all that is necessary is that a collimated supersonic ( > c_s) beam be set up within a scale R_* 1 kpc.

One obvious question concerns the possible seriousness of Kelvin-Helmolts instabilities in the vortex sheet between the beam and the external medium or cocoon. This has been discussed by Turland and Scheuer [8] and Blandford and Pringle [9], but until the physics of the boundary layer can be understood, or some relevant experiments can be performed, the stability of the supersonic portion of the flow must remain an open question. Nevertheless, the calculations and general physical arguments do indicate that very high Mach number flows are more likely to be stable for longer distances than mildly supersonic and subsonic jets. This is an argument in favor of a collimation mechanism in which there is no subsonic regime in the flow.

The linear sizes of the hot spots in the active sources are typically 3 kpc, and a perfectly isentropic fluid beam would in fact be focussed to a width 100 pc, and so there is some leeway for beam widening by entrainment processes and shock heating. At the hot spots, it is presumed that the bulk energy is efficiently randomised either through a strong transverse shock or by surface disruption of the beam. The general type of flow pattern expected would involve a shock where the beam energy is randomised, a contact discontinuity between shocked beam material and the external medium, and a stand-off shock moving into the extragalactic medium (whose ambient sound speed is << V). This pattern is illustrated in refs. [7 - 10] (though we would expect much greater irregularities and asymmetries in any real situation).

While it is conceivable that the magnetic field in radio sources was already present in the extragalactic medium, it can readily have been transported out from the galactic nucleus along with the beam. As discussed by Blandford and Rees [7], if the central engine produces a wind in which magnetic and kinetic energy densities are comparable, this ratio can be preserved (or even enhanced) despite many orders of magnitude decrease in the plasma density as the beam moves outward: although the parallel component of B drops as r^-2, the perpendicular component goes as r^-1 as the beam widens. The magnetic field would thus be predominantly transverse to the source axis in the beam and in the hot-spots; in the cocoon it would be sheared into a direction tangential to the boundary (consistent with what is observed). Note that such shearing motion can amplify a field up to equipartition, but that its dynamical effects then provide feedback which prevents it from ever becoming stronger. Although the field would have a preferred orientation, leading to high linear polarization of the synchrotron radiation, there may be many reversals. The scale of such reversals would depend on the character of the central source. If the "hot fluid" in the beam were supplied by multiple supernovae, or resulted from tidal disruption of random stars by a massive black hole, then the sign of the magnetic flux would be uncorrelated over scales containing 10⁵³ erg of energy; but a more organised field could arise if the power supply involved a single massive object, or accretion from the general interstellar medium in the central galaxy.

It is unclear what mechanism reconverts the bulk kinetic energy of the beam into relativistic electrons (with the requisite power-law spectrum) at the "working surface", but the kind of acceleration which almost certainly attains 1 percent efficiency in, for instance, the supernova remnant Cass A (where the velocities are only 0.02c) could be even more effective behind shock fronts where the velocities are much higher. Recently, some very suggestive arguments have been proposed [11, 12] according to which relativistic particles can be accelerated with roughly the observed spectrum by shock fronts.

If the flow pattern were sufficiently stable, a typical double source would evolve towards increasing size as the "hot spots" move outward, leaving a sheath or cocoon of lower surface brightness along their track; but eventually the central source would switch off, the residual relativistic plasma expanding and merging into the intergalactic medium. (The final stages of this process, and its cumulative impact on the intergalactic medium, deserve further study). The precise time-dependence of source size and radio luminosity depends on the external density, on how well the beams are collimated, etc. If this type of model applies to the "giant" double source 3C 236, the beams must have lasted, with mean power ~ 10⁴⁵ erg s^-1 for 10⁸ yr.

Among the uncertainties and complications that bedevil any comparison with real double sources are the following:

(i) Instabilities are bound to complicate the flow pattern. (One would in fact wish to invoke some instabilities in order to explain the irregular and asymmetric structure of real sources. Also, the fact that the "hot spots" are not even smaller can best be explained by supposing that instabilities at the beam boundary have led to frictional heating and entrainment which causes r to increase faster than in the idealised isentropic case.) We are pessimistic about the prospects of firm theoretical progress in this area: it is hard enough to reproduce observed phenomena even in controlled experimental situations (water jets, etc.); and in the radio source context not only is the physics more complex (effects of compressibility, magnetic fields, etc.) but the relevant parameters (external gas density, pressures, etc.) are themselves uncertain. Perhaps wind-tunnel experiments may provide a closer analogy to real sources than the over-idealised models amenable to theoretical study.

(ii) The central power supply may have fluctuated over the source lifetime (and the distinction between an unsteady beam and a "multiple plasmoid" model [13] is only semantic as long as the interval between ejection of the plasmoids is short enough for a permanent channel through the surrounding medium to be maintained.

(iii) Asymmetry or instabilities of the collimation process may make the intensity of the two beams unequal. Conceivably "flip-flop" behaviour, where the plasma outflow squirts alternately in two opposite directions [14], could explain jets such as those in 3C 273, M87, and NGC 6251.

(iv) Inhomogeneities in the extragalactic medium may cause complex structure in the hot spots, as is seen in 3C 390.3: part of the beam may lag behind the rest, or be deflected, if it encounters a dense external cloud.

(v) Transverse motions of the external medium relative to the galaxy could destroy the symmetry or linear structure, especially when the beam is so weak, or so poorly collimated, that its speed of advance is the transverse velocity. This is perhaps relevant to the interpretation of "radio trails", as we discuss more fully below. Transverse or shearing motions of the external medium would particularly affect the final stages of a source's life when the expansion is slower. Buoyancy effects whose role in radio source morphology was first emphasised by Gull and Northover [15] - may also be significant, especially for sources in clusters or associated with unusually massive galaxies. Diffusive escape of relativistic particles may be important in large "relaxed" doubles if the streaming speed of the electrons is limited to the Alfven speed. So if all the relativistic electrons in an extended source like DA 240 originate in a central hot spot, either large-scale convective motion or re-acceleration is called for.

If the beams varied on timescales 10⁴ - 10⁷ yr for the reasons cited under (ii) or (iii), the cocoon, which delineates the path traced out by the hot spots over the history of the source, would be non-uniform: it would be particularly conspicuous in places where the hot spots were located at times of high beam intensity. The cocoon could thus resemble a series of blobs linking each outer hot spot to the central galaxy. (This is perhaps relevant to the interpretation of so-called "double doubles".)