2. BLACK HOLE DEMOGRAPHICS: HIGH REDSHIFT QSOs

The existence of SBHs in the nuclei of nearby galaxies has gained popular consensus only in recent years. That supermassive black holes must power QSO activity has, however, been widely suspected since the mid 1960s (e.g. Robinson et al. 1965). It is therefore not surprising that the first studies of black hole demographics were conducted, over two decades ago, using optical counts of high redshift QSOs. In a seminal paper entitled "Masses of Quasars", Andrzej Soltan (1982) proposed a simple argument: QSO optical number counts yield a QSO luminosity function which can be integrated to give a mean comoving energy density in QSO light. After applying the appropriate bolometric corrections and assuming a reasonable conversion factor of mass into energy, Soltan concluded that the SBHs powering high redshift (z > 0.3) QSOs comprise a total mass density of ~ 5 × 10⁴ M Mpc^-3, each SBH having a mass of 10⁸ - 10⁹ M. Soltan's arguments, which have been employed many times in the following years (Chokshi & Turner 1992; Small & Blandford 1992; Salucci et al. 1999), lead to the inescapable conclusion that most, if not all, nearby galaxies must host dormant black holes in their nuclei. This finding has been the main driver for SBH searches in nearby quiescent galaxies and has kindled the interest in the accretion crisis in nearby galactic nuclei (Fabian & Canizares 1988), ultimately leading to the revival of accretion mechanisms with low radiative efficiencies (Rees et al. 1982, Narayan & Yi 1994).

Armed with recent measurements of the QSO luminosity function from the 2dF QSO Survey (0.3 < z < 2.3, Boyle et al. 2000) and the Sloan Digital Sky Survey (3.0 < z < 5.0, Fan et al. 2001), we are in a position to update Soltan's results. If (L, z) is the QSO luminosity function, the cumulative mass density in SBHs which power QSO activity can be expressed as:

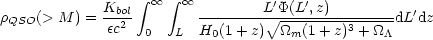
(1)

where the mass accretion rate is simply = K_bol L^-1 c^-2, with K_bol the bolometric correction (from Elvis et al. 1986), and the energy conversion coefficient (assumed equal to 0.1). An = 0.0, _m = 1.0, H₀ = 75 km s^-1 Mpc^-1 cosmology is assumed for consistency in comparing the results with those derived in the following sections. The cumulative mass density due to QSO accretion is shown in Fig. 1. It should be noted that the magnitude limits of the 2dF and Sloan QSO surveys correspond to Eddington limits on the SBHs masses of 4.5 × 10⁷ M and 7.3 × 10⁸ M respectively. Cumulative mass densities down to 10⁶ M are calculated on the (unverified) assumption that the QSO luminosity function holds at the corresponding magnitude (B ~ -19). Furthermore, the lower redshift limit of integration for the SDSS luminosity function was pushed down to the high redshift boundary of the 2dF survey (z = 2.3), although there are no QSO luminosity functions covering the 2.3 < z < 3.0 range. For masses larger than 10⁸ M, the extrapolation from z = 3 to z = 2.3 of the spatial density (e.g. Fig. 3 of Fan et al. 2001) or mass density (Fig. 7 in these proceedings) as a function of redshift from the SDSS joins rather smoothly the curve derived from the 2dF survey, therefore our assumption is likely justified. However, for smaller masses or luminosities, the SDSS mass density, extrapolated to z ~ 2.3, overpredicts the QSO mass density (per unit redshift) derived from the 2dF data by an order of magnitude. Thus, it is likely that the linear rise of the SBH cumulative mass density for the high redshift QSOs between 10⁸ and 10⁶ M represents an upper bound to the real curve, which could have been overestimated by a factor of a few (i.e., up to ~ three).

Figure 1. Comparison between the black hole mass function in high redshift QSOs (blue lines - dotted line: 2dF sample; dashed line: SDSS sample; solid line: both samples combined); local AGNs (red) and local quiescent galaxies (black, corresponding to the dotted black line in Fig. 4).

In short, the cumulative mass density from the optical QSO counts due to accretion onto high redshift QSOs (0.3 < z < 5.0) appears to be in the range (2 - 4) × 10⁵ M Mpc^-3. Notice that this estimate does not account for the possibility that sizable black holes might have already been in place before the optically bright phase of QSOs. Furthermore, I have neglected the contribution to the SBH mass density from the so called "obscured" or "Type II" QSOs, the existence of which is required to explain the observed properties of the X-ray background. In analogy with local Seyfert 1 and Seyfert 2 galaxies, in Type II QSOs molecular material, with column density in the neighborhood of 10²³ cm^-2, completely hides the nucleus from view at optical wavelengths (e.g. Fabian & Iwasawa 1999). The contribution of Type II QSOs could be significant. For instance, Barger et al. (2001) calculate lower and upper limits of 6 × 10⁴ and 9 × 10⁵ M Mpc^-3 for the mass density in the SBHs which comprise the X-ray background. Gilli, Salvati & Hasinger (2001) find that the spectral shape of the hard (2-10 Kev) X-ray background can be best explained if obscured AGNs evolve more rapidly as a function of redshift than do their unobscured counterparts. Their model assumes a ratio between absorbed and unabsorbed AGNs increasing from ~ 4 in the local universe to ~ 10 at z ~ 1.3, and remaining constant at higher redshifts. Such a model, if correct, would translate into an increase by nearly a factor of 10 in the SBH cumulative mass density derived above.