5.1.4. Dynamics of Bars. III. N-Body Models

In the next section I will examine the internal dynamics of NGC 936 in more detail. This includes a comparison with n-body models. The only rotating models which have been published in sufficient detail for this comparison are due to Miller and Smith (1979, hereafter MS) and to Hohl and Zang (1979, hereafter HZ). Both models were originally calculated to study the formation of elliptical galaxies, but both were given relatively large amounts of rotation, and turned out to rotate more rapidly than most ellipticals (see Fig. 46). We will see below and in section 5.1.5 that they are instead fairly good first-order models of bars.

Figure 44 shows two views of the MS bar, one seen pole-on and one seen approximately in the same way as NGC 936. Several features of the velocity field of NGC 936 are seen in the model. The streaming motions in the bar frame are approximately symmetric around the major axis and fastest along the minor axis. This implies that the orbits are elongated parallel to the bar, a result which is confirmed by illustrations of the orbits (Figures 5 and 7 of MS). When the model is viewed with an orientation like that in NGC 936, the isovelocity contours are close to radial, as discussed in the previous section. Miller and Smith note that the zero-velocity contour is twisted from the photometric minor axis toward the apparent major axis of the bar. Qualitatively there is therefore reasonably good agreement between the velocity fields of the model and of NGC 936. The density distributions differ somewhat in that the model bar is less elongated and especially in that it is not flat. The model is also less centrally concentrated, although (1) this is inevitable because of the finite cell size used in the calculations, and (2) it is more the bulge than the bar of NGC 936 which is centrally concentrated.

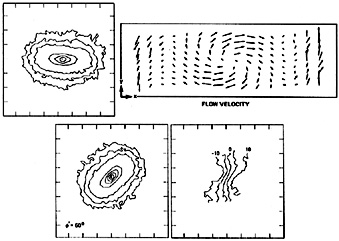Figure 44. Density and velocity distributions in the Miller and Smith (1979) bar model. The upper-left panel shows contours of equal projected density as seen along the rotation axis. The axial ratio of the bar is ~ 0.5. The upper-right panel is the unprojected flow field in the equational plane, shown in a frame of reference rotating (clockwise) with the bar. The residual streaming is in the rotation direction. Corotation is clearly visible. The lower two panels show contours of equal projected density and velocity as seen at i = 45°, ' = 60°. For NGC 936, i = 49° and ' = 66°. This figure is taken from Figures 4, 10 and 11 of Miller and Smith (1979).

The comparison made in the next section and in Kormendy (1982b) shows that the MS model and model IV of HZ are very similar. The initial conditions are also similar, except in one respect. Both models begin with ~ 10⁵ particles of equal mass distributed uniformly inside a sphere. Both models initially rotate with a constant angular velocity which is almost equal to the value ₀ which balances the cold system against gravity in the equatorial plane: / ₀ = 1 in MS and / ₀ = 0.866 in HZ. The basic difference is that the MS bar is initially much colder, with a ratio of energy in random motions to that in gravitational potential of T / |W| = 1/360, compared with T / |W| = 1/8 in HZ. However, both models collapse violently along the rotation axis, and both are equally hot by the time that bar formation is complete (see below). The similarity of the two models is an encouraging sign that their properties and their implications regarding the structure of bars are fairly general.