4.5. The Angular size - redshift relation

Another potentially sensitive test of models is related to the fact that the angular size of an extended object D located at a redshift z, depends rather sensitively on the properties of the cosmological model in which it is being measured. Knowing the absolute size of an object (e.g. galaxy or radio source) and the angle subtended by a distribution of such objects in the universe, it may be possible (after correcting for projection and evolution effects) to say something about the geometry of space and the matter content of the universe.

It is easy to derive a relationship between D and . Consider an object of proper length D at a coordinate distance r, and assume for simplicity that the object is aligned along the axis so that coordinates marking its `top' and `bottom' are respectively (r, ₁ + ₁, ₁) and (r, ₁, ₁). The observer is at r = 0. The proper length of the object can be obtained by setting t = constant in the FRW line-element (2) giving [142]

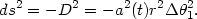
(46)

As a result we get the following expression for the angle subtended by the object at the location of the observer

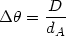
(47)

where d_A = a(t)r is the `angular-size distance'. Since 1 + z = a₀ / a(t) one gets d_A = d_L(1 + z)^-2, where d_L(z) = a₀r(1 + z) is the luminosity distance discussed in the previous section. Accordingly (47) may be rewritten as

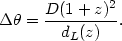
(48)

In Fig 10 we have plotted the angular size - redshift relation for flat cosmological models with a cosmological constant. (We have used expressions (28) for the luminosity distance d_L and (19) for the dimensionless Hubble parameter h(z), assuming a flat universe _total = _m + = 1.)

Figure 10. The angular size is shown as a function of cosmological redshift z for flat cosmological models with a cosmological constant m + = 1. Heavier lines correspond to larger values of m. For comparison we also show (dashed line) the angular size in a de Sitter universe ( = 1).

We find that as the object is moved to higher redshifts its angular size first decreases (as naively expected) but soon begins to increase after passing through a minimum value. The appearance of a minimum angular size at a given redshift z_min is a generic feature of cosmological models with _m > 0. Differentiating (48) with respect to the redshift after substituting for d_L from (30), and then setting / z = 0 gives z_min = 1.25 for the flat matter dominated Einstein-de Sitter universe. From figure 10 we find that the location of the minimum angular size moves to higher redshifts as is increased, until in the limiting case = 1 there is no minimum at all. (Formally z_min in de Sitter space, indicating that the angular size of an object decreases monotonically with redshift without ever reaching a minimum value.)

The suggestion that angular sizes of galaxies could be used to discriminate between cosmological models was first made in [95]. Curiously the angular size of a typical galaxy at a redshift z ~ 1 is roughly one arc second which is close to the limiting value of the angular resolution (`seeing') allowed by the Earth's atmosphere Einstein is quoted as saying [154]. Beyond z ~ 1 the angular size of an object increases, and if one is confident that galaxies of a given class at higher redshifts are similar in form to their lower redshift counterparts, then this test can in principle provide a powerful means of discriminating between world models especially with the use of satellite data which can get around the `seeing' limit. Other (larger) objects which can be used to probe the angular size-redshift relation include clusters of galaxies [142] and both extended and compact radio galaxies [105, 31]. Extended radio sources which include the twin radio lobes surrounding a radio galaxy can have sizes ranging from a few kpc to ~ 1000 kpc, consequently the typical angular size of such objects is ~ 20 arc seconds which can easily be measured using ground based techniques.

However, a word of caution must now be added, both clusters and radio galaxies are prone to strong evolutionary effects which could lead to a change in size over cosmological epoch. Thus a comprehensive understanding of physical effects associated with both clusters (subclustering, virialization etc.) and radio galaxies (evolution of radio lobes and the central engine etc.) is necessary before the angular size-redshift relation can be used to unambiguously determine cosmological parameters including .

Recently Kellerman (1993) and Gurvits et al. (1998) have studied the angular sizes of compact radio sources (QSO's and AGN's) arguing that the central `engine' powering these objects is likely to be controlled by a limited number of physical parameters (mass of central black hole, accretion rate etc.) and may therefore be subject to less evolutionary effects than extended radio sources. On the basis of an analysis of a large number of sources spanning a wide redshift range 0.01 < z < 4.73 these authors claim that an increase in the angular size has been detected which is consistent with _m ~ 1. (However working with the same data set as Kellerman (1993), Kayser (1995) has shown that a significant cannot be ruled out.)

An interesting feature of closed universes not present in the flat models considered in figure 10, or in open models, is the presence of antipodal points. The presence of antipodes can contribute to changing the angular size as well as to the lensing of a source galaxy or quasar [80] and therefore provide us with a good means to constrain closed cosmological models. A metric describing the closed FRW universe is

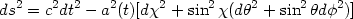
(49)

where 0 , , 0 2. If we assume that the observer is located at = 0 then the associated antipodal point is at _a = . Substituting ds² = 0 we obtain = dt / a, where is the conformal time coordinate. In a matter dominated universe the form for the expansion factor is a() = A(1 - cos), ct = A( - sin), and the Hubble parameter is given by H sin / (1 - cos) where 0 2. Thus a light ray from the antipodal point _a = reaches = 0 at the time of maximum expansion = (corresponding to H = 0). Consequently in a matter dominated closed universe, light from an antipodal point can never reach an observer during the expanding phase (when H > 0). This situation changes when one considers a closed universe with a cosmological term. In this case the universe is not obliged to recollapse and one can observe an antipodal point during the expansion epoch. The location of antipodal points can be derived from the following considerations: from (28) we find for a closed universe

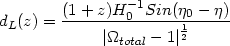
(50)

where

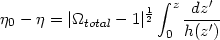
(51)

since d_A = d_L(1 + z)^-2 it follows that for

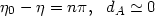
(52)

and, from (47), , i.e. the angular size of an object located close to one of the antipodal points (52) can become very large. Consequently such an object will appear to us to be extremely bright even if located at a high redshift ! The presence of `normal' galaxies and quasars, as well as gravitationally lensed objects out to redshifts 4.92 set a lower limit on the antipodal redshift z_a(, _m) > 4.92 which can be used to constrain the cosmological parameter pair (, _m) in a closed universe [51, 124, 147]. (Multiple images of a source object located further away than the antipodal redshift z_a are very difficult to form [80].) Since the supernovae analysis prima-facie appears to favour a closed universe, antipodal constraints may be used to further narrow down the allowed range in parameter space.