As we saw in the last two sections, the vacuum associated with both one-loop quantum effects and models with spontaneous symmetry breaking, has properties identical to those of a cosmological constant. There is one problem however, in the case of zero-point fluctuations, the vacuum density turns out to be infinite leading to an infinitely large cosmological term and resulting in a cosmological constant problem for cosmology (see section 5). Assuming that the ultraviolet divergences responsible for the cosmological constant problem can be cured by (hitherto unknown) physics occurring near the Planck scale, one gets a finite but very large value
|
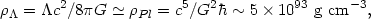
where
Pl
is the Planck density. On the other hand, as we saw earlier,
recent observations of the luminosities of high redshift
supernovae combined with CMB results give the
following value for the dimensionless density in
|
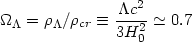
where cr
= 3H2 /
8
G = 1.88 ×
10-29h2 g/cm3 (see
sections 4.3 &
4.4), which leads to
Pl
× 10-123, i.e. the value of the cosmological
constant today is almost 123 orders of magnitude smaller than
the Planck density !
As we have shown in section 6,
a large (negative) value of the vacuum energy also arises in models with
spontaneous symmetry breaking. In this case, the fine tuning involved
in matching the present value of
to observations
depends upon
the symmetry breaking scale, and ranges from 1 part in 10123
for the Planck scale, to 1 part in 1053 for the electroweak
scale.
Clearly the question begging an answer is:
which physical processes can generate a small value for
today
without necessarily involving a delicate fine tuning of initial
conditions?
Although no clear cut answers are available at the time of writing
(it may even be that a very small
may demand
completely new physics) some avenues which could lead us to interesting
answers will be explored in this section.