8.2. When may a -term be described by a minimally coupled scalar field?

Now let us consider the following important question: can a -term always be described by a minimally coupled scalar field, for any observed behaviour of a(t) or H(a) ? To answer this question let us first consider the equations of motion describing a FRW universe with matter (dust) _m and a scalar field

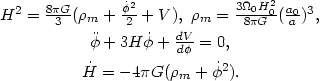
(96) (97)

The clue to whether a -term can be successfully described by a minimally coupled field is provided by the background equation for 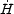which we rewrite in the following form changing the independent variable from t to a ( = 0 is assumed):

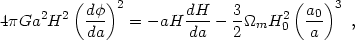
(98)

where a₀ is the present value of the FRW scale factor a(t) and _m includes all dust-like matter at present (CDM, baryons, sufficiently massive neutrinos, etc.). Since the left-hand side of Eq. (98) is always non-negative therefore so is the right-hand side. From this follows a fundamental restriction on the expansion law for the Universe, which we write in terms of the following inequality on the redshift dependence of the Hubble parameter H(z), 1 + z a₀ / a:

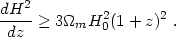
(99)

Actually, Eq. (99) is nothing more than the weak energy condition for a lambda-field: + p 0.

This inequality saturates in the case of a constant -term (a cosmological constant). Equation (99) constitutes the necessary condition for an arbitrary H(z) dependence to be physically described by a minimally coupled scalar field (in the absence of spatial curvature). It will be shown below that Eq. (99) is also a sufficient condition, since a knowledge of H(z) and _m permits a unique reconstruction of the self-interaction potential V() of this scalar lambda-field (see section 8.4). Taken at z = 0, Eq. (99) reduces to the following relation between the acceleration parameter q₀ and _m:

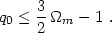
(100)

It should be emphasized that we have no idea at present whether or not Eqs. (99, 100) are fulfilled. Only future observations will tell us that. Moreover, as was explained in previous sections, a constant -term fits existing data very well. Thus, we know already that the inequalities (99, 100) are close to saturation. So, it will be not an easy observational task. In this case, the presence of even a small spatial curvature may dramatically change our conclusions.

In the case of non-zero spatial curvature ( 0), Eq. (99) generalizes to:

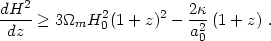
(101)

Therefore, if future data show that the inequality (99) is not valid, one has either to invoke a positive spatial curvature for the Universe ( = 1), or else to discard this model entirely and to consider a more complicated model of a -term, modelled by, say, a scalar-field non-minimally coupled to gravity. It is easy to verify that in the case of R² / 2 coupling, no necessary conditions such as (99) or (101) appear. However, as was mentioned above, this type of coupling is strongly restricted by observational data [33].

An interesting example of dissipationless decay of a lambda-field is provided by Peebles and Ratra (1988) who consider a minimally coupled scalar field rolling down a potential

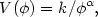
subject to the equation of motion

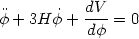
(102)

(k and are constants, we set M_P = 1 for simplicity). Let us assume that the energy density of the scalar field

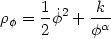
(103)

is subdominant at early epochs (as demanded by CMB and nucleosynthesis constraints) so that < _B at z >> 1, where _B is the density of background matter driving the expansion of the universe. Assuming a general expansion law for the universe a(t) t^q the field equation of motion (102) becomes

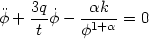
(104)

which has the solution

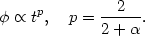
(105)

Substituting in (103) we find t^{2p - 2}, as a result if p > 0 the scalar field density decreases more slowly than the background density of matter or radiation which decreases as _B t^-2. Consequently we find

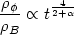
(106)

i.e. for > 0 the scalar field density can dominate the matter/radiation density at late times even if it was subdominant to begin with [163, 155]. (This attractive property of scalar fields is occasionally referred to as `quintessence'.) The rate of growth of / <sub>m,r</sub> can be modulated by `tuning' the value of . Another way of arriving at this conclusion is to examine the equation of state of the scalar field while the latter is subdominant, this turns out to be

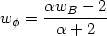
(107)

where w_B is the background equation of state. From (107) we find w < w_B i.e. the equation of state of the scalar field is less stiff than that of matter driving expansion. The conservation condition _,B a^{-3[1 + w_{(, B)}]} now guarantees that the scalar field will come to dominate the expansion dynamics of the universe even if it was initially subdominant. As a result can be significantly small during the radiation dominated epoch to satisfy nucleosynthesis constraints yet be large enough today to give rise to an accelerating universe in agreement with recent supernovae results. (Once begins to dominate the energy density, the universe enters into a period of accelerated expansion driven by the scalar field energy density which begins to mimic an effective -term.)

A different possibility arises if we consider a scalar field rolling down an exponential potential

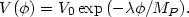
In the case of a flat universe, the scalar field density scales exactly like the background density of matter driving the expansion of the universe so that the ratio of the scalar field density to the total matter density rapidly approaches a constant value [163, 63, 64]

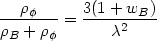
(108)

(w_B = 0, 1/3 respectively for dust, radiation). This `tracker-like' quality whereby the scalar field contributes the same fixed amount to the total matter density allows it to play the role of a form of dark matter. However strong constraints on this model come from cosmological nucleosynthesis which suggests / _B 0.2. ⁽¹⁴⁾ As a result the scalar field in these models is forever destined to remain subdominant, it can neither dominate the matter density of the universe nor give rise to its accelerated expansion rate.

A potential which interpolates between an exponential and a power law is

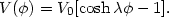
(109)

Since V() exp , for >> 1, we would expect this potential to reproduce features of the exponential potential discussed earlier. As a result / _B constant and w w_B, if the scalar field commences rolling from a large initial value. As the scalar field rolls down towards smaller values, the potential begins to resemble the Inflationary `chaotic' form V() <sup>2 2</sup>, leading to late-time Inflation during which w - 1. Finally oscillations of the scalar field give rise to a `dust-like' phase during which w 0.

An unusual potential with interesting features was proposed in [215]

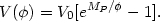
(110)

However, the requirement that << 1 during the matter dominated epoch, while ~ 1 nowadays, is fulfilled for this potential only if the present value of is significantly larger than M_Pl. Thus, for practical applications in the present universe, this potential shows little difference from the inverse-power-law potential V ^-1.

A useful property of potentials (102), (109) & (110) is that they significantly alleviate the fine tuning problem associated with generating a small cosmological term at precisely the present epoch. As a result, can come to dominate the current cosmological density from a fairly general class of initial conditions. A phase space analysis of scalar field models was carried out in [163, 63, 64, 125] where it was shown that both exponential and negative power-law potentials display appealing attractor-like qualities. However, despite the many attractive features of `quintessence' models a degree of fine tuning does remain in fixing the parameters of the potential and has been commented on in [125, 118].

It is worth pointing out in this context that the energy density of relic gravity waves created during Inflation (_g) behaves like a tracker field since _g / _B constant, if the expansion factor grows exponentially during Inflation [2]. For more realistic situations in which the inflaton field rolls down its potential slowly the ratio _g / _B increases with time with the result that the graviton energy density may become comparable to _B at very late times provided Inflation commenced at the Planck epoch [168]. COBE measurements of the large angle anisotropy of the cosmic microwave background (CMB) however ensure that the gravity wave contribution to the total matter density is negligibly small today: _g 10^-12 [178]. However the intriguing possibility that quanta of a different type of fundamental field (the dilaton perhaps) may come to dominate the energy density of the universe without necessarily violating CMB bounds remains to be investigated.

Some cosmological consequences of scalar field models and models with a decaying cosmological term have been analyzed in [155, 75, 140, 177, 36, 69, 70, 23] [24, 202, 98, 34, 96, 77, 156, 201, 203]. Candidates for quintessence based on high energy physics and string theory are discussed in [35, 118] and non-minimal scalar field models are treated in [74, 33].

Phenomenological models usually belong to the general category of models in which matter either violates or marginally satisfies the strong energy condition (SEC) + 3P 0. Scalar fields driving inflation as well as the models discussed earlier in this section furnish examples of matter which can violate the SEC. Other examples of such `strange' or `exotic' forms of matter include cosmic strings and domain walls. The field configuration within a string is in the false vacuum state leading to P = - along the string length. A network of random non-intercommuting strings therefore possesses the average equation of state P = - / 3 which marginally satisfies the SEC [197]. The mean energy density of a string network dominated by straight strings decays as a^-2 leading to the linear expansion law a t [197, 79]. Similarly P = - is satisfied along any two orthogonal directions within a domain wall leading to P = - 2 / 3 for a network of walls [197, 180] and resulting in `mild' Inflation a^-1, a t². The presence of tangled strings and/or domain walls can be tested by measurements sensitive to the expansion dynamics of the universe. For instance recent supernovae results strongly suggest w - 2/3 which severely constraints the string network for which w - 1/3. Thus it appears that a tangled network of strings is ruled out by current observations (see section 4.3).

Table 1. Summary of phenomenological models. Here a is the scale factor, H the Hubble parameter, T the temperature, t the cosmic time (A, B, are constants).

Evolutionary relation for (t)	Reference
t-2	[59, 25, 16, 15, 13, 133, 147]
t-	[14, 103, 104]
A + B exp(-t)	[14, 181]
a-2	[133, 148, 149, 1, 199, 32, 79, 116]
a-	[143, 151, 169, 135, 138, 176, 177] [93, 102, 147, 193, 23, 24, 202, 96, 77]
exp(-a)	[162]
T	[25, 107]
H2	[127, 207, 208, 63, 42]
H2 + Aa-	[3, 28, 172, 200]
f (H)	[128, 129]
g(, H)	[89, 164]

A brief summary of some models with a decaying cosmological term is given in Table 1 (adapted from [147]), we should stress that most of these models are phenomenological and are therefore not necessarily backed by strong physical arguments.

Finally one should mention another phenomenological approach tied to the possibility of a cosmological term decaying and transferring its energy into articles and/or radiation [148, 68]. Observationally such an approach can, in principle, be tested: in the case of dissipative, baryon number conserving decay of a -term into baryons and antibaryons, the subsequent annihilation of matter and antimatter would result in a homogeneous gamma-ray flux which could be constrained by observations of the diffuse gamma-ray background in the Universe [68, 138]. A decay of the cosmological term directly into radiation could be probed by cosmic microwave background anisotropies, cosmological nucleosynthesis etc. [68, 174, 17, 146, 138, 151, 176, 177].