


3.3. Reconstructing the cosmic equation of state
Although fundamental theories such as Supergravity or M-theory do provide a
number of possible candidates for quintessence they do
not uniquely predict its potential
V( ). Therefore it
becomes meaningful
to reconstruct V(
). Therefore it
becomes meaningful
to reconstruct V( )
and the cosmic equation of state w = P /
)
and the cosmic equation of state w = P /
 directly from observations in a model independent manner
[49,
50,
51,
52].
This is possible to do if one notices that the scalar field potential
as well as its equation of state can be directly expressed in terms
of the Hubble parameter and its derivative
directly from observations in a model independent manner
[49,
50,
51,
52].
This is possible to do if one notices that the scalar field potential
as well as its equation of state can be directly expressed in terms
of the Hubble parameter and its derivative
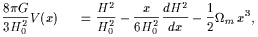
| (13) |
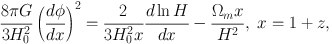
| (14) (15) |
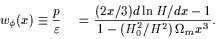
| (16) |
Since the Hubble parameter is related to the luminosity distance
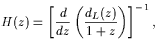
| (17) |
one can determine both the quintessence potential
V( ) as well as
reconstruct its equation of state
w
) as well as
reconstruct its equation of state
w (z) provided
the luminosity distance dL(z) is
known from observations. A three parameter ansatz for estimating the
luminosity distance was proposed in
[49].
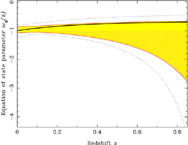
Results from that paper reproduced in
figure 3 indicate that only a small amount of
evolution in
w
(z) provided
the luminosity distance dL(z) is
known from observations. A three parameter ansatz for estimating the
luminosity distance was proposed in
[49].
Results from that paper reproduced in
figure 3 indicate that only a small amount of
evolution in
w (z)
is permitted by current SnIa observations. The presence of
a cosmological constant is therefore in good agreement with these results.
(z)
is permitted by current SnIa observations. The presence of
a cosmological constant is therefore in good agreement with these results.
|
Figure 3. The equation of state of dark
energy/quintessence is reconstructed from observations
of Type Ia high redshift supernovae in a model independent manner.
The equation of state satisfies
-1 |
A word of caution should be added: as
shown in figure 4 a near degeneracy exists
between the equation of state of dark energy and the value of
 m.
The latter should therefore be known to better than 5% accuracy for
the reconstruction program to yield very accurate results
(see also
[51]).
m.
The latter should therefore be known to better than 5% accuracy for
the reconstruction program to yield very accurate results
(see also
[51]).
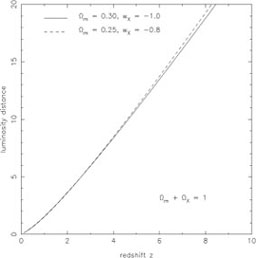
|
Figure 4. The near degeneracy in the
luminosity distance is shown for the pair of cosmological models with
{ |