5.4.5. Diffusion and settling of heavy ions
At the same temperature, heavy ions will move more slowly than light ions, and all ions will move more slowly than electrons. As a result, the heavy ions will tend to settle towards the center of the cluster. This settling is generally halted when it results in an electric field large enough to balance the extra gravitational force on the heavier ions. Models for the distribution of heavy elements in clusters, assuming that settling has occurred rapidly enough to reach this equilibrium, are discussed in Section 5.5.6 below. Here, the rate of settling will be considered.
Heavy ions that diffuse toward the cluster center rapidly reach a drift velocity at which gravitational acceleration is balanced by the slowing effect of collisions (Fabian and Pringle, 1977; Rephaeli, 1978). Using the expression for the mean free path of a slow moving heavy ion in a plasma (Spitzer, 1956), we obtain the drift velocity vD,
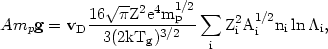
| (5.48) |
where A and z are the heavy ion atomic number and charge, g is the gravitational acceleration, Tg is the gas temperature, and the sum is over the various ions in the plasma. Assuming cosmic abundances, one finds
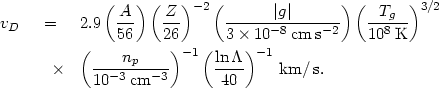
| (5.49) |
The values of A and z in equation (5.49) are those for fully ionized iron. The X-ray lines of iron are the strongest lines observed from clusters, and have been detected in a large number of clusters (Section 4.3.2). These lines play an important role in considerations of the origin and energetics of the intracluster gas (Section 5.10), and thus the distribution of iron is particularly important. As noted by Rephaeli (1978), the value of the drift velocity in equation (5.49) is considerably smaller than the value given by Fabian and Pringle (1977) because they failed to include helium and heavier elements in the slowing time.
According to equation (5.49), the drift velocity depends on the cluster gravitational potential and the density and temperature of the intracluster gas. If the cluster potential is given by the King analytic approximation to the isothermal distribution (equations 2.13, 5.59), then the largest value of g occurs at roughly the core radius rc (actually r = 1.027rc), and
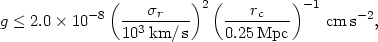
| (5.50) |
where 
r is
the radial velocity dispersion of the cluster. The time to drift in a
small distance dr is then dt= dr/vD. If
one sets dr
rc,
then the drift time is
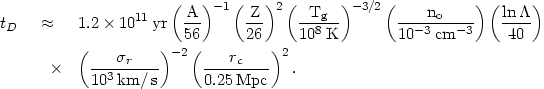
| (5.51) |
If the intracluster gas is adiabatic (constant entropy per particle;
Section 5.5),
then np
Tg3 / 2, and the variation of these two
quantities does not affect the
drift time. If the gas is isothermal, then the reduction of density with
distance from the cluster center shortens the drift time, although the
increase in the
distance to be traversed and the decrease in the gravitational
acceleration more than make up for this.
Rephaeli (1978)
has integrated the drift time for a
variety of equations of state for the gas, and finds that the drift
times from
radii greater than four core radii in to one core radius is always greater
than 1011 yr times the cluster parameters in equation (5.51),
with the
gas density and temperature evaluated at the cluster center. Since this
means the drift time is generally at least ten times the probable age
of the cluster, the settling of iron into the cluster center is unlikely to
occur.
As noted by Rephaeli (1978), the presence of a magnetic field in the intracluster gas would inhibit the sedimentation of iron even further. The situation is similar to that for thermal conduction (Section 5.4.3); iron ions could only drift along the direction of magnetic field lines. Unless the magnetic field were predominately radial, settling of iron would be very strongly inhibited. The effect is even larger than that on thermal conduction, because the sedimentation of iron ions requires that the individual ions drift over large distances, while heat can be conducted from the inner to the outer portions of a cluster without having an individual electron traverse these distances. For example, loop structures in the magnetic field would tend to prevent any sedimentation beyond the bottom of the loop.
Although it appears unlikely that heavy elements like iron would have settled to the cluster center, this does not mean that the abundance of heavy elements is necessarily uniform. Heavy elements might be concentrated in the cluster core if they were injected into the intracluster gas in the core. If the heavy elements were produced in stars within galaxies, as is usually assumed (Sections 4.3.2 and 5.10), then this gas might have been predominantly deposited in the cluster core because either ram pressure or collisional stripping will occur more easily there. Of course, if all the intracluster gas were produced by this mechanism, then no abundance gradients would be produced if all galaxies in the cluster contained gas with the same average abundances. If, however, the intracluster medium were partly due to heavy element containing gas stripped from galaxies, and partly due to heavy element lacking intergalactic gas that fell into the cluster, and if the stripping were concentrated at the cluster core, then a gradient in the abundance of heavy elements could result (Nepveu, 1981b). Subsequent mixing of the intracluster gas (Section 5.4.6 below) might still destroy such abundance variations.
Such an abundance gradient could greatly reduce the amount of iron needed to produce the observed iron lines. If the iron were concentrated at the cluster core, it would all be located in regions of high electron density, so that the iron line emissivity per iron ion would be higher than the average emissivity per hydrogen ion (Section 5.2). The amount of iron needed to produce the observed iron lines could be reduced by as much as a factor of 20 (Abramopoulos et al., 1981). Since the production of a nearly solar abundance of iron is one of the major problems with galaxy formation in clusters and the origin of the intracluster gas, the possibility that the real abundance might be much lower is very important. Unfortunately, all of the available spectra of the 7 keV iron line in clusters have been made with low spatial resolution detectors, which do not provide sufficient information on the location of the iron. The observation of spatially resolved spectra of clusters including the 7 keV iron line are critically important to our understanding of clusters, and will be possible if the AXAF satellite is launched (Chapter 6).